הבדלים בין גרסאות בדף "אינטגרל לא מסויים/דוגמאות"
(←פתרון (לא מלא)) |
(←פתרון (לא מלא)) |
||
| שורה 258: | שורה 258: | ||
ואז, '''הצבה 3:''' <math>k=e^{2u}</math> | ואז, '''הצבה 3:''' <math>k=e^{2u}</math> | ||
| + | |||
מכאן זו פונקציה רצינואלית של ליניארי חלקי פולינום ממעלה 2, זה לא בעיה בהשוואה למה שהלך למעלה. | מכאן זו פונקציה רצינואלית של ליניארי חלקי פולינום ממעלה 2, זה לא בעיה בהשוואה למה שהלך למעלה. | ||
גרסה מ־15:32, 5 במאי 2012
תוכן עניינים
1
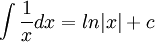
2
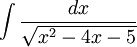
פתרון
השלמה לריבוע והצבה ראשונה:
הדבר הראשון שנעשה הוא התהליך של השלמה לריבוע, שבסופו נקבל כי:
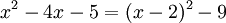
ולכן ההצבה הראשונה שנעשה תהא: 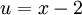 , וכמובן קל להבין כי
, וכמובן קל להבין כי 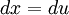 .
.
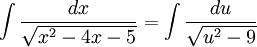
פונקציות טריגונומטריות היפרבוליות (הערה):
ניעזר בתכונות של 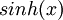 ושל
ושל 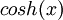 :
:
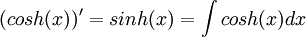
וכן בזהות: 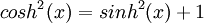
הצבה שנייה:
נציב: 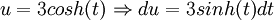
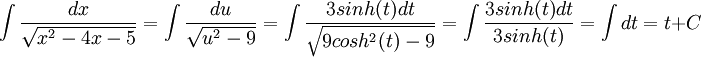
ולהחזיר את t לx, אני משאיר לכם (:
3
האינטגרל הבא לקוח מספר התרגילים של בועז צבאן (1.24, אם אינני טועה)
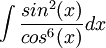
פתרון
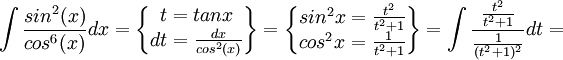
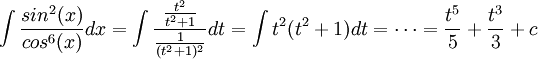
- יש טעות בהצבה של
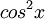 , שכן
, שכן 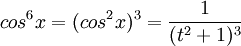
- יש טעות בהצבה של
- אבל צריך לקחת בחשבון גם את הdt
- צודק. נראה לי שאם אני לא ראיתי את זה, גם אחרים לא יראו ;)
- אבל צריך לקחת בחשבון גם את הdt
4
בדומה לאינטגרל הקודם, לקוח מבועז צבאן (1.27)
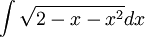
דרך א'
א. ניתן להשתמש בהצבת אוילר, אבל אנחנו ננקוט בטקטיקה שונה.
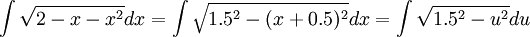
הצבה ראשונה: 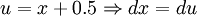
הצבה שנייה: 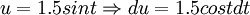
ואם נחזור לחישוב האינטגרל,
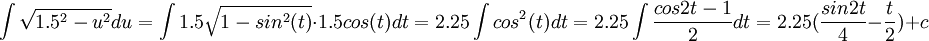
ומכאן מעבירים את t לx.
דרך ב'
ההצבה הראשונה נשארת כפי שהייתה, אך הפעם לא נעשה הצבה שניה אלא נשתמש באינטגרציה בחלקים:
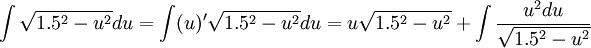
כעת נוכל להבחין כי מתקיים:
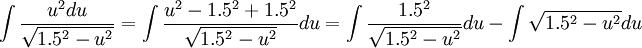
כעת נביט רק על האינטגרל הראשון ונציב: 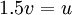
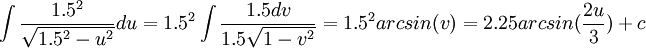
אם נחזור לאינטגרל המקורי נקבל:
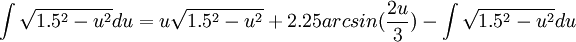
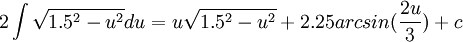
וסיימנו (:
5
אינטגרל חביב שנלקח ממבחן בחדו"א בב"ג (של מדעי המחשב)
![\int \frac{dx}{x+\sqrt[n]{x}}](/images/math/d/6/b/d6ba1b541269fe1e6be09b7380e6ea54.png) כאשר
כאשר 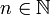 .
.
פתרון
הכוונה היא עבור n>1, עבור n=1 תסתכלו בדוגמא הראשונה.
![\int \frac{dx}{x+\sqrt [n]{x}}=\begin{Bmatrix}
t^{n}=x\\
nt^{n-1}dt=dx
\end{Bmatrix}
=\int \frac{nt^{n-1}}{t^{n}+t}dt=n\int \frac{t^{n-2}}{t^{n-1}+1}dt=
\begin{Bmatrix}
k=t^{n-1}+1\\
dk=(n-1)t^{n-2}dt
\end{Bmatrix}=](/images/math/f/2/5/f25f53ffba17c08dd00c9d738f81d881.png)
![\int \frac{dx}{x+\sqrt [n]{x}}=\frac{n}{n-1}\int \frac{dk}{k}=\frac{n}{n-1}ln|k|+c= \frac{n}{n-1}ln|x^{\frac {n-1}{n}}+1|+c](/images/math/4/0/4/404302f30574fb18ef2f9d0fda5f54df.png)
6
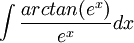
פתרון
ניעזר באינטגרציה בחלקים.
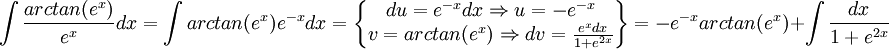
פתאום זה נראה יותר אנושי, כעת נסתכל על האינטגרל שנותר:
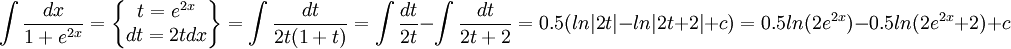
כל שנותר הוא לאחד את התוצאות, ולקבל את התוצאה הסופית.
7
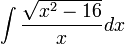
פתרון
נעשה את ההצבה הבאה: 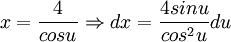
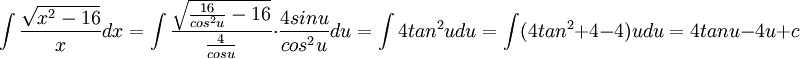
תחזירו לx לבד, בכל מקרה אני עצלן ואף אחד לא יקרא את זה!
8
אחד קליל מהחוברת של בועז (:,
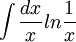
פתרון
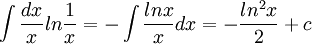
9
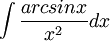
פתרון
ראשית נפעיל אינטגרציה בחלקים כאשר: 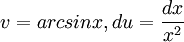
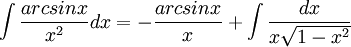
כעת נחשב את האינטגרל השני שקיבלנו:
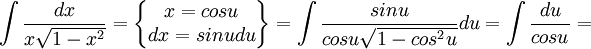
וכעת ניעזר בהצבה האוניברסלית כדי למצוא את האינטגרל החדש:
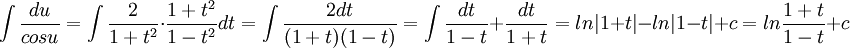
כרגיל להחזיר ולהנות (:
10
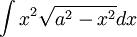
הצבה 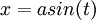
11
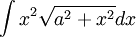
הצבה היפרבולית 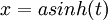 .
.
12
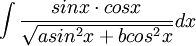
פתרון
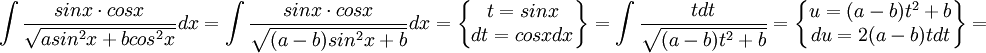
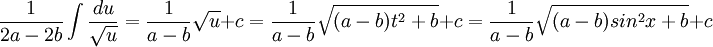
פתרון (יותר מוצלח כמסתבר)
להציב 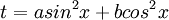
13
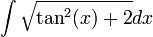
פתרון (לא מלא)
זה לקח לי שני עמודים בכתב יד, זה נורא (אני בטוח שיש פתרון יותר חכם)
הצבה 1: 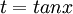
הצבה 2: 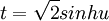
אח"כ צריך לשחק עם מה שמקבלים (לפי תכונות של קוסינוס וסינוס היפרבולי), ואז להעביר את זה לייצוג המקורי.
ואז, הצבה 3: 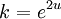
מכאן זו פונקציה רצינואלית של ליניארי חלקי פולינום ממעלה 2, זה לא בעיה בהשוואה למה שהלך למעלה.
במקרה הכי גרוע, תהיה הצבה 4.
14
![\int \frac{1}{\sqrt[4]{sin(x)^3cos(x)^5}} dx](/images/math/8/7/4/874a4afa3ca6ad39e9d7d1fafcf03997.png)