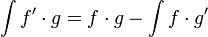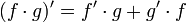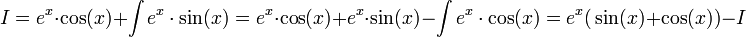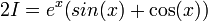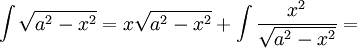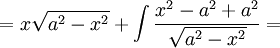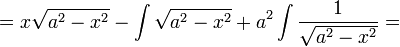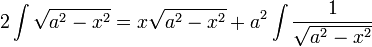הבדלים בין גרסאות בדף "אינטגרציה בחלקים"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) מ |
|||
| שורה 1: | שורה 1: | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
==הגדרה== | ==הגדרה== | ||
| − | '''אינטגרציה בחלקים''' הוא כינוי | + | '''אינטגרציה בחלקים''' הוא כינוי לנוסחת האינטגרציה הבאה: |
| − | + | :<math>\int{f'\cdot g}=f\cdot g-\int{f\cdot g'}</math> | |
| − | הנוסחא נובעת מיידית | + | הנוסחא נובעת מיידית מנוסחת גזירת כפל: |
| − | + | :<math>(f\cdot g)'=f'\cdot g+g'\cdot f</math> | |
==דוגמאות== | ==דוגמאות== | ||
| − | א. בדוגמא זו ניתן לראות שאפשר להעלים גורם אחד על ידי גזירתו. | + | א. בדוגמא זו ניתן לראות שאפשר להעלים גורם אחד על-ידי גזירתו. יתכן ונדרש בדוגמאות מסוג זה לבצע את הפעולה מספר פעמים, אך בדוגמא זו הסתפקנו בפעם אחת בלבד. |
| − | <math>\int{ | + | <math>\int{x\cdot\cos(x)}=?</math> |
| − | נסמן <math>f'=cos(x),g=x</math> | + | נסמן <math>f'=\cos(x)\ ,\ g=x</math> |
| − | ולכן <math>f=sin(x),g'=1</math> | + | ולכן <math>f=\sin(x)\ ,\ g'=1</math> |
| − | + | לפי נוסחת אינטגרציה בחלקים מתקיים | |
| − | + | :<math>\int{x\cdot\cos(x)}=x\cdot\sin(x)-\int{\sin(x)}=x\cdot\sin(x)+\cos(x)+C</math> . | |
| + | ב. בדוגמא הבאה לא ניתן להעלים גורם על-ידי גזירה, אולם עדיין ניתן להעזר באינטגרציה בחלקים לפתרון הבעיה. | ||
| + | <math>\int{e^x\cdot\cos(x)}=?</math> | ||
| − | + | נסמן <math>I=\int{e^x\cdot\cos(x)}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | נסמן | + | |
| − | + | ||
| − | + | ||
לכן | לכן | ||
| − | + | :<math>I=e^x\cdot\cos(x)+\int{e^x\cdot\sin(x)}=e^x\cdot\cos(x)+e^x\cdot\sin(x)-\int{e^x\cdot\cos(x)}=e^x\big(\sin(x)+\cos(x)\big)-I</math> | |
ולכן | ולכן | ||
| − | + | :<math>2I=e^x\big(sin(x)+\cos(x)\big)</math> | |
ומכאן יוצא | ומכאן יוצא | ||
| − | + | :<math>\int{e^x\cdot\cos(x)}=I=\frac{e^x\big(\sin(x)+\cos(x)\big)}{2}+C</math> . | |
| − | + | ג. בדוגמא הבאה נראה שניתן להתייחס לכפל בקבוע <math>1</math> כנגזרת של הפונקציה <math>x</math> ובכך "להמציא" גורם שיעזור לנו בפתרון הבעיה באמצעות אינטגרציה בחלקים. | |
| − | + | ||
| − | ג. בדוגמא הבאה נראה שניתן להתייחס לכפל בקבוע 1 כנגזרת של הפונקציה x ובכך "להמציא" גורם שיעזור לנו בפתרון | + | |
<math>\int{\sqrt{a^2-x^2}}=?</math> | <math>\int{\sqrt{a^2-x^2}}=?</math> | ||
| − | נסמן <math>f'=1,g=\sqrt{a^2-x^2}</math> | + | נסמן <math>f'=1\ ,\ g=\sqrt{a^2-x^2}</math> |
| − | ולכן <math>f=x,g'=\frac{-x}{\sqrt{a^2-x^2}}</math> | + | ולכן <math>f=x\ ,\ g'=\frac{-x}{\sqrt{a^2-x^2}}</math> |
| − | נפעיל | + | נפעיל נוסחת אינטגרציה בחלקים: |
| − | + | :<math>\int{\sqrt{a^2-x^2}}=x\sqrt{a^2-x^2}+\int{\frac{x^2}{\sqrt{a^2-x^2}}}=</math> | |
| − | + | :<math>=x\sqrt{a^2-x^2}+\int{\frac{x^2-a^2+a^2}{\sqrt{a^2-x^2}}}=</math> | |
| − | + | :<math>=x\sqrt{a^2-x^2}-\int{\sqrt{a^2-x^2}}+a^2\int{\frac1{\sqrt{a^2-x^2}}}=</math> | |
ולכן סה"כ, בדומה לדוגמא הקודמת | ולכן סה"כ, בדומה לדוגמא הקודמת | ||
| − | + | :<math>2\int{\sqrt{a^2-x^2}}=x\sqrt{a^2-x^2}+a^2\int{\frac1{\sqrt{a^2-x^2}}}</math> | |
| − | + | ||
| − | כאשר את האינטגרל האחרון נלמד ב[[שיטת ההצבה]] | + | כאשר את האינטגרל האחרון נלמד ב[[שיטת ההצבה]]. |
גרסה מ־00:41, 27 בינואר 2016
הגדרה
אינטגרציה בחלקים הוא כינוי לנוסחת האינטגרציה הבאה:
הנוסחא נובעת מיידית מנוסחת גזירת כפל:
דוגמאות
א. בדוגמא זו ניתן לראות שאפשר להעלים גורם אחד על-ידי גזירתו. יתכן ונדרש בדוגמאות מסוג זה לבצע את הפעולה מספר פעמים, אך בדוגמא זו הסתפקנו בפעם אחת בלבד.
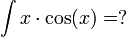
נסמן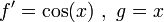 
ולכן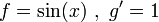 
לפי נוסחת אינטגרציה בחלקים מתקיים
.
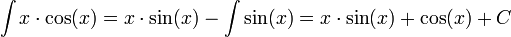ב. בדוגמא הבאה לא ניתן להעלים גורם על-ידי גזירה, אולם עדיין ניתן להעזר באינטגרציה בחלקים לפתרון הבעיה.
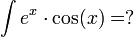
נסמן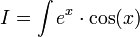 
לכן
ולכן
ומכאן יוצא
.
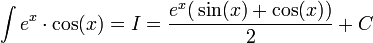ג. בדוגמא הבאה נראה שניתן להתייחס לכפל בקבוע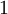 
כנגזרת של הפונקציה 
ובכך "להמציא" גורם שיעזור לנו בפתרון הבעיה באמצעות אינטגרציה בחלקים.
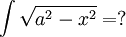
נסמן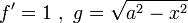 
ולכן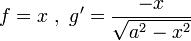 
נפעיל נוסחת אינטגרציה בחלקים:
ולכן סה"כ, בדומה לדוגמא הקודמת
כאשר את האינטגרל האחרון נלמד בשיטת ההצבה.
