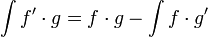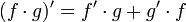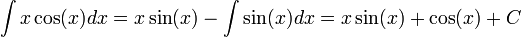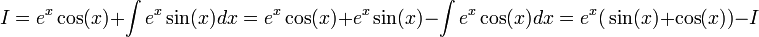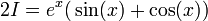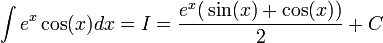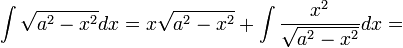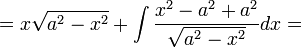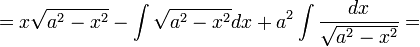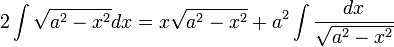הבדלים בין גרסאות בדף "אינטגרציה בחלקים"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(יצירת דף עם התוכן "==הגדרה== '''אינטגרציה בחלקים''' הוא כינוי לנוסחאת האינטגרציה הבאה: ::<math>\int{f'g}=fg-\int{fg'}</math> הנו...")
 
 
(4 גרסאות ביניים של 2 משתמשים אינן מוצגות)
שורה 1: שורה 1:
 +
[[קטגוריה:אינפי]]
 
==הגדרה==
 
==הגדרה==
−
'''אינטגרציה בחלקים''' הוא כינוי לנוסחאת האינטגרציה הבאה:
+
'''אינטגרציה בחלקים''' הוא כינוי לנוסחת האינטגרציה הבאה:
  
−
::<math>\int{f'g}=fg-\int{fg'}</math>
+
:<math>\int{f'\cdot g}=f\cdot g-\int{f\cdot g'}</math>
  
−
הנוסחא נובעת מיידית מנוסחאת גזירת כפל:
+
הנוסחא נובעת מיידית מנוסחת גזירת כפל:
−
::<math>(fg)'=f'g+g'f</math>
+
:<math>(f\cdot g)'=f'\cdot g+g'\cdot f</math>
  
−
==דוגמאות==
+
הנוסחא נכונה במידה והאינטגרלים מוגדרים, ובפרט עבור <math>f,g</math> בעלות נגזרות רציפות.
−
א. בדוגמא זו ניתן לראות שאפשר להעלים גורם אחד על ידי גזירתו. ייתכן ונדרש בדוגמאות מסוג זה לבצע את הפעולה מספר פעמים, אך בדוגמא זו הסתפקנו בפעם אחת בלבד.
+
  
−
<math>\int{xcos(x)}=?</math>
+
(אחרת, אמנם יש קדומה ל- <math>f'\cdot g+g'\cdot f</math> , אבל לא בהכרח ל- <math>f'\cdot g</math> ו- <math>g'\cdot f</math> בנפרד.)
  
−
נסמן <math>f'=cos(x),g=x</math>
+
==דוגמאות==
 +
א. בדוגמא זו ניתן לראות שאפשר להעלים גורם אחד על-ידי גזירתו. יתכן ונדרש בדוגמאות מסוג זה לבצע את הפעולה מספר פעמים, אך בדוגמא זו הסתפקנו בפעם אחת בלבד.
  
−
ולכן <math>f=sin(x),g'=1</math>
+
<math>\int x\cos(x)dx=?</math>
  
−
ולפי נוסחאת אינטגרציה בחלקים מתקיים
+
נסמן <math>f'=\cos(x)\ ,\ g=x</math>
  
−
::<math>\int{xcos(x)}=xsin(x)-\int{sin(x)}=xsin(x)+cos(x)+C</math>
+
ולכן <math>f=\sin(x)\ ,\ g'=1</math>
  
 +
לפי נוסחת אינטגרציה בחלקים מתקיים
  
 +
:<math>\int x\cos(x)dx=x\sin(x)-\int\sin(x)dx=x\sin(x)+\cos(x)+C</math>
  
  
−
ב. בדוגמא הבאה לא ניתן להעלים גורם על ידי גזירה, אולם עדיין ניתן להעזר באינטגרציה בחלקים לפתרון הבעייה.
+
ב. '''חזרה למקורות''' - בדוגמא הבאה לא ניתן להעלים גורם על-ידי גזירה, אולם חזרה לאינטגרל המקורי פותרת לנו את הבעיה.
  
−
<math>\int{e^xcos(x)}=?</math>
+
<math>\int e^x\cos(x)dx=?</math>
  
−
נסמן  
+
נסמן <math>I=\int e^x\cos(x)dx</math>
−
 
+
−
::<math>I=\int{e^xcos(x)}</math>
+
  
 
לכן
 
לכן
  
−
::<math>I=e^xcos(x)+\int{e^xsin(x)}=e^xcos(x)+e^xsin(x)-\int{e^xcos(x)}=e^x\Big(sin(x)+cos(x)\Big)-I</math>
+
:<math>I=e^x\cos(x)+\int e^x\sin(x)dx=e^x\cos(x)+e^x\sin(x)-\int e^x\cos(x)dx=e^x\big(\sin(x)+\cos(x)\big)-I</math>
  
 
ולכן
 
ולכן
  
−
::<math>2I=e^x\Big(sin(x)+cos(x)\Big)</math>
+
:<math>2I=e^x\big(\sin(x)+\cos(x)\big)</math>
  
 
ומכאן יוצא
 
ומכאן יוצא
  
−
::<math>\int{e^xcos(x)}=I=\frac{e^x\Big(sin(x)+cos(x)\Big)}{2}+C</math>
+
:<math>\int e^x\cos(x)dx=I=\frac{e^x\big(\sin(x)+\cos(x)\big)}{2}+C</math>
  
 +
ג. בדוגמא הבאה נראה שניתן להתייחס לכפל בקבוע <math>1</math> כנגזרת של הפונקציה <math>x</math> ובכך "להמציא" גורם שיעזור לנו בפתרון הבעיה באמצעות אינטגרציה בחלקים.
  
 +
<math>\int\sqrt{a^2-x^2}dx=?</math>
  
−
ג. בדוגמא הבאה נראה שניתן להתייחס לכפל בקבוע 1 כנגזרת של הפונקציה x ובכך "להמציא" גורם שיעזור לנו בפתרון הבעייה באמצעות אינטגרציה בחלקים.
+
נסמן <math>f'=1\ ,\ g=\sqrt{a^2-x^2}</math>
  
−
<math>\int{\sqrt{a^2-x^2}}=?</math>
+
ולכן <math>f=x\ ,\ g'=-\frac{x}{\sqrt{a^2-x^2}}</math>
  
−
נסמן <math>f'=1,g=\sqrt{a^2-x^2}</math>
+
נפעיל נוסחת אינטגרציה בחלקים:
  
−
ולכן <math>f=x,g'=\frac{-x}{\sqrt{a^2-x^2}}</math>
+
:<math>\int\sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}+\int\frac{x^2}{\sqrt{a^2-x^2}}dx=</math>
  
−
נפעיל את נוסחאת אינטגרציה בחלקים:
+
:<math>=x\sqrt{a^2-x^2}+\int\frac{x^2-a^2+a^2}{\sqrt{a^2-x^2}}dx=</math>
  
−
::<math>\int{\sqrt{a^2-x^2}}=x\sqrt{a^2-x^2}+\int{\frac{x^2}{\sqrt{a^2-x^2}}}=</math>
+
:<math>=x\sqrt{a^2-x^2}-\int\sqrt{a^2-x^2}dx+a^2\int\frac{dx}{\sqrt{a^2-x^2}}=</math>
−
 
+
−
::<math>=x\sqrt{a^2-x^2}+\int{\frac{x^2-a^2+a^2}{\sqrt{a^2-x^2}}}=</math>
+
−
 
+
−
::<math>=x\sqrt{a^2-x^2}-\int{\sqrt{a^2-x^2}}+a^2\int{\frac{1}{\sqrt{a^2-x^2}}}=</math>
+
  
  
 
ולכן סה"כ, בדומה לדוגמא הקודמת
 
ולכן סה"כ, בדומה לדוגמא הקודמת
  
−
::<math>2\int{\sqrt{a^2-x^2}}=x\sqrt{a^2-x^2}+a^2\int{\frac{1}{\sqrt{a^2-x^2}}}</math>
+
:<math>2\int\sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}+a^2\int\frac{dx}{\sqrt{a^2-x^2}}</math>
−
 
+
  
−
כאשר את האינטגרל האחרון נלמד ב[[שיטת ההצבה]]
+
כאשר את האינטגרל האחרון נלמד ב[[שיטת ההצבה]].

גרסה אחרונה מ־11:11, 3 בנובמבר 2016

הגדרה

אינטגרציה בחלקים הוא כינוי לנוסחת האינטגרציה הבאה:

\int{f'\cdot g}=f\cdot g-\int{f\cdot g'}

הנוסחא נובעת מיידית מנוסחת גזירת כפל:

(f\cdot g)'=f'\cdot g+g'\cdot f

הנוסחא נכונה במידה והאינטגרלים מוגדרים, ובפרט עבור 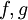f,g בעלות נגזרות רציפות.

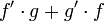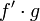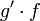(אחרת, אמנם יש קדומה ל- f'\cdot g+g'\cdot f , אבל לא בהכרח ל- f'\cdot g ו- g'\cdot f בנפרד.)

דוגמאות

א. בדוגמא זו ניתן לראות שאפשר להעלים גורם אחד על-ידי גזירתו. יתכן ונדרש בדוגמאות מסוג זה לבצע את הפעולה מספר פעמים, אך בדוגמא זו הסתפקנו בפעם אחת בלבד.

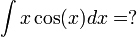
\int x\cos(x)dx=?

נסמן 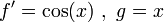f'=\cos(x)\ ,\ g=x

ולכן 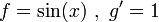f=\sin(x)\ ,\ g'=1

לפי נוסחת אינטגרציה בחלקים מתקיים

\int x\cos(x)dx=x\sin(x)-\int\sin(x)dx=x\sin(x)+\cos(x)+C


ב. חזרה למקורות - בדוגמא הבאה לא ניתן להעלים גורם על-ידי גזירה, אולם חזרה לאינטגרל המקורי פותרת לנו את הבעיה.

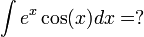
\int e^x\cos(x)dx=?

נסמן 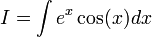I=\int e^x\cos(x)dx

לכן

I=e^x\cos(x)+\int e^x\sin(x)dx=e^x\cos(x)+e^x\sin(x)-\int e^x\cos(x)dx=e^x\big(\sin(x)+\cos(x)\big)-I

ולכן

2I=e^x\big(\sin(x)+\cos(x)\big)

ומכאן יוצא

\int e^x\cos(x)dx=I=\frac{e^x\big(\sin(x)+\cos(x)\big)}{2}+C

ג. בדוגמא הבאה נראה שניתן להתייחס לכפל בקבוע 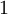1 כנגזרת של הפונקציה 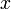x ובכך "להמציא" גורם שיעזור לנו בפתרון הבעיה באמצעות אינטגרציה בחלקים.

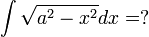
\int\sqrt{a^2-x^2}dx=?

נסמן 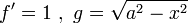f'=1\ ,\ g=\sqrt{a^2-x^2}

ולכן 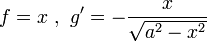f=x\ ,\ g'=-\frac{x}{\sqrt{a^2-x^2}}

נפעיל נוסחת אינטגרציה בחלקים:

\int\sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}+\int\frac{x^2}{\sqrt{a^2-x^2}}dx=
=x\sqrt{a^2-x^2}+\int\frac{x^2-a^2+a^2}{\sqrt{a^2-x^2}}dx=
=x\sqrt{a^2-x^2}-\int\sqrt{a^2-x^2}dx+a^2\int\frac{dx}{\sqrt{a^2-x^2}}=


ולכן סה"כ, בדומה לדוגמא הקודמת

2\int\sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}+a^2\int\frac{dx}{\sqrt{a^2-x^2}}

כאשר את האינטגרל האחרון נלמד בשיטת ההצבה.

מקור: https://math-wiki.com/index.php?title=אינטגרציה_בחלקים&oldid=68092