אינפי 1, תשנ"ו מועד ב' - פתרון (זלצמן)
קישור לבחינה עצמה: המבחן
אתם מוזמנים לעזור בפתרון, לשנות, לתקן ולהעיר הערות.
שאלה 1
יהי 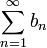 טור חיובי.
טור חיובי.
א. הראה שאם 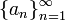 סדרה המקיימת לכל
סדרה המקיימת לכל  :
: 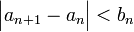 וכן
וכן 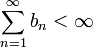 אזי הסדרה מתכנסת.
אזי הסדרה מתכנסת.
- הוכחה
אם הטור מתקיים התנאים הנ"ל כלומר: 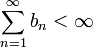 וגם
וגם 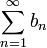 טור חיובי, אזי הטור מתכנס. שכן סדרת הסכומים החלקיים שלו היא מונוטונית עולה וחסומה מלעיל ולכן מתכנסת.
טור חיובי, אזי הטור מתכנס. שכן סדרת הסכומים החלקיים שלו היא מונוטונית עולה וחסומה מלעיל ולכן מתכנסת.
נוכיח כי הסדרה הנה קושי וזאת באמצעות הקריטריון של קושי להתכנסות סדרות.
יהי 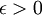 . לפי קריטריון קושי קיים
. לפי קריטריון קושי קיים 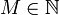 כך שלכל
כך שלכל 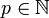 מתקיים
מתקיים 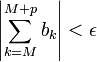 .
.
יהיו 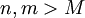 , אזי:
, אזי:
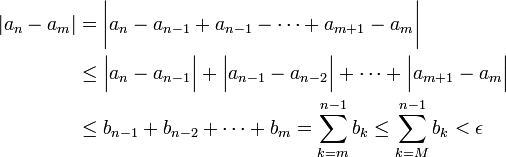
הראנו שהסדרה היא קושי ולכן מתכנסת.
- דרך אחרת
נשים לב כי 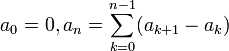 , וכיון שהטור הזה מתכנס בהחלט כי בהחלט הוא נשלט על-ידי
, וכיון שהטור הזה מתכנס בהחלט כי בהחלט הוא נשלט על-ידי 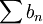 כך גם
כך גם 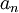 מתכנסת כי התכנסות של טור שקולה להתכנסות של הסכומים החלקיים.
מתכנסת כי התכנסות של טור שקולה להתכנסות של הסכומים החלקיים.
ב. אם הטור 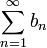 אז קיימת סדרה
אז קיימת סדרה 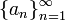 המקיימת לכל
המקיימת לכל
 :
: 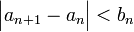 וגם מתבדרת.
וגם מתבדרת.
- הוכחה
נביט בסדרת הסכומים החלקיים של הטור (עם שינוי קל): 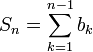 ונגדיר
ונגדיר 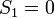
הטור 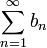 מתבדר ולכן לפי ההגדרה (כי הוספת איבר אחד בהתחלה אינה משפיעה על התכנסות או התבדרות הסדרה) הסדרה מתבדרת.
מתבדר ולכן לפי ההגדרה (כי הוספת איבר אחד בהתחלה אינה משפיעה על התכנסות או התבדרות הסדרה) הסדרה מתבדרת.
כמו כן, קל לראות כי מתקיים התנאי: 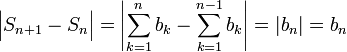

- תיקון
תהי 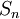 סדרת הסכומים החלקיים של הטור
סדרת הסכומים החלקיים של הטור 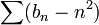 הטור מתבדר כהפרש של טור מתבדר בטור מתכנס מתקיים
הטור מתבדר כהפרש של טור מתבדר בטור מתכנס מתקיים 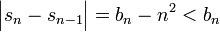
שאלה 2
בדוק התכנסות והתכנסות בהחלט של הטורים הבאים:
א. 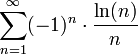
- פתרון
ראשית נבדוק התכנסות בהחלט: 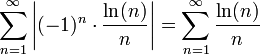
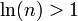 לכל
לכל 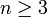 ולכן לכל
ולכן לכל  שכזה מתקיים:
שכזה מתקיים: 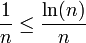 ולפי מבחן ההשוואה הראשון הטור מכיון שהטור ההרמוני מתבדר אז
ולפי מבחן ההשוואה הראשון הטור מכיון שהטור ההרמוני מתבדר אז 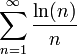 מתבדר.
מתבדר.
ידוע 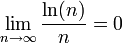 (ואם אתם לא מאמינים לי אפשר להוכיח את זה עם לופיטל) ולכן מספיק להוכיח שהסדרה מונוטונית יורדת כדי להסיק התכנסות בתנאי לפי לייבניץ:
(ואם אתם לא מאמינים לי אפשר להוכיח את זה עם לופיטל) ולכן מספיק להוכיח שהסדרה מונוטונית יורדת כדי להסיק התכנסות בתנאי לפי לייבניץ:
נביט בפונקציה 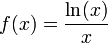 , מספיק להראות כי
, מספיק להראות כי 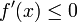 כאשר
כאשר 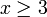 .
.
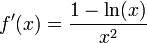 וקל לראות שהתנאי לעיל מתקיים עבור
וקל לראות שהתנאי לעיל מתקיים עבור 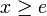 ובפרט עבור
ובפרט עבור 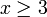 .
.
ב. 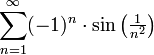
- פתרון
נראה התכנסות בהחלט לפי מבחן ההשוואה הגבולי
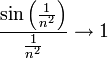 ולכן הטורים חברים.
ולכן הטורים חברים.
מכיון 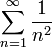 מתכנס אז גם
מתכנס אז גם 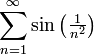 .
.
ולכן הטור מתכנס בהחלט.
ג. 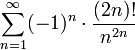
- פתרון
נוכיח התכנסות בהחלט לפי מבחן המנה של ד'לאמבר
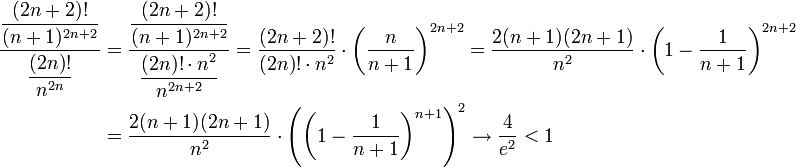
ולכן הטור מתכנס בהחלט!
שאלה 3
ציטוט משפטים
שאלה 4
יש לבדוק האם הפונקציות הבאות רבמ"ש בקטעים הנתונים:
א. 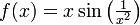 בקטע
בקטע 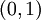
נראה שהגבולות בקצוות הקטע סופיים ולכן הפונקציה רבמ"ש:
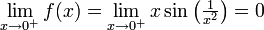 , חסומה כפול 0.
, חסומה כפול 0.
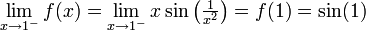 . מזאת מכיון שהפונקציה היא מנה, הרכבה וכפל של פונקציות רציפות.
. מזאת מכיון שהפונקציה היא מנה, הרכבה וכפל של פונקציות רציפות.
ב. 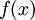 מסעיף א' בקרן
מסעיף א' בקרן 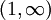
בדומה לסעיף הקודם, נראה שהגבולות בקצוות הקטע סופיים ולכן הפונקציה רבמ"ש:
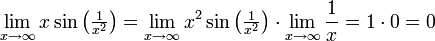
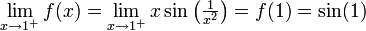 . מזאת מכיון שהפונקציה היא מנה, הרכבה וכפל של פונקציות רציפות.
. מזאת מכיון שהפונקציה היא מנה, הרכבה וכפל של פונקציות רציפות.
ג. 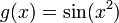 רבמ"ש בקרן
רבמ"ש בקרן 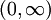
נניח בשלילה שהפונקציה רבמ"ש. הפונקציה 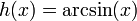 רציפה בתחום
רציפה בתחום ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) ולכן רבמ"ש בו.
ולכן רבמ"ש בו.
מכיון שהתחום ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) הנו התמונה של
הנו התמונה של 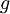 , ההרכבה של הפונקציות רבמ"ש (לפי משפט).
, ההרכבה של הפונקציות רבמ"ש (לפי משפט).
לכן 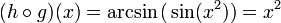 רבמ"ש, בסתירה להוכחה מהתירגול.
רבמ"ש, בסתירה להוכחה מהתירגול.
- פתרון נוסף (עם סדרות)
נגדיר את שתי הסדרות הבאות:
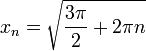 ואת הסדרה
ואת הסדרה 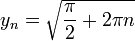 ונמשיך מכאן...
ונמשיך מכאן...
שאלה 5
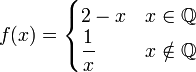
צריך למצוא עבור אילו ערכים הפונקציה רציפה ועבור אילו ערכים הפונקציה גזירה.
- פתרון
נתחיל עם הנקודות עבורן הפונקציה רציפה, שכן זהו תנאי הכרחי לגזירות.
הנקודות בהן הפונקציה רציפה הן הנקודות בהן מתקיים השוויון: 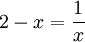
בכל שאר הנקודות, ניתן לבנות שתי סדרות: אחת של רציונאליים ואחת של אי-רציונאליים שתמונותיהן יתכנסו לשני ערכים שונים ולכן היא אינה רציפה בהן.
במקרה של שוויון, כל סדרה של רציונאליים, אי-רציונאליים או שילוב שלהם תתכנס ל- 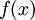 בין אם הוא רציונאלי או לא.
בין אם הוא רציונאלי או לא.
נפתור את המשוואה ונקבל תוצאה יחידה: 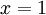 , בנקודה זו הפונקציה רציפה.
, בנקודה זו הפונקציה רציפה.
כעת נבדוק האם היא גזירה בנקודה זו, אם הפונקציה גזירה אזי בהכרח 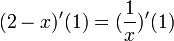 מנימוקים דומים, כלומר:
מנימוקים דומים, כלומר:
מכיון שהגבולות 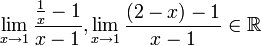
אז לפי היינה התמונות של כל הסדרות שמתכנסות ל-1 יתכנסו לגבולות האלו. אם הפונקציה גזירה, בהכרח הגבול קיים ולכן כל הסדרות התמונות חייבות להתכנס לאותה נקודה. על כל פנים, נחזור לשוויון שהצגנו לעיל:
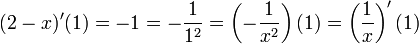
ולכן הפונקציה גזירה בנקודה 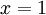 .
.
שאלה 6
א.
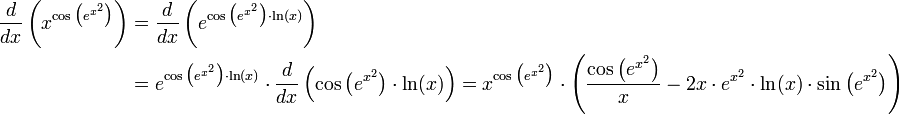
ב.
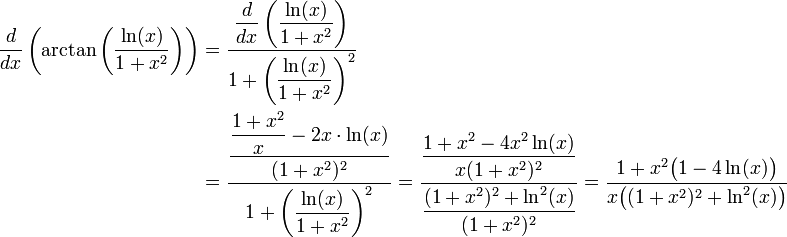
ג.