אלגברה מופשטת 1- מועד א' קיץ תשע"ג
מתוך Math-Wiki
גרסה מ־20:52, 5 בספטמבר 2013 מאת Ofekgillon10 (שיחה | תרומות) (יצירת דף עם התוכן "==שאלה 2== ===סעיף א'=== הוכח את משפט אוילר על החזקות ופתור את המשוואה <math>16x\equiv 29!\cdot 25^{92} \operatorname{...")
שאלה 2
סעיף א'
הוכח את משפט אוילר על החזקות ופתור את המשוואה 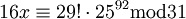
פתרון
משפט אוילר על החזקות אומר שאם 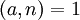 אז
אז 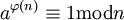 . אבל אם
. אבל אם 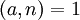 אז לפי משפט,
אז לפי משפט, 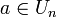 . אחת התוצאות של משפט לגרנז' אומרת שאם מעלים איבר בחזקת סדר של החבורה, נקבל את הנטרלי של החבורה. במקרה הזה, הנטרלי הוא 1 והסדר של החבורה הוא
. אחת התוצאות של משפט לגרנז' אומרת שאם מעלים איבר בחזקת סדר של החבורה, נקבל את הנטרלי של החבורה. במקרה הזה, הנטרלי הוא 1 והסדר של החבורה הוא 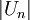 . נזכור שההגדרה של
. נזכור שההגדרה של 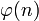 היא בעצם
היא בעצם 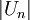 ולכן קיבלנו
ולכן קיבלנו 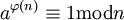 .
.
כעת נפתור את המשוואה. כיוון ש- 31 ראשוני, אז לפי משפט וילסון, 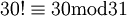 וכיוון ש-30 הפיך ב-
וכיוון ש-30 הפיך ב- 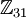 אפשר להסיק ש-
אפשר להסיק ש- 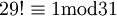 . קיבלנו:
. קיבלנו: 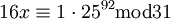 .
.
נזכור ש- 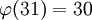 (אם p ראשוני אז
(אם p ראשוני אז 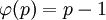 ) ולכן לפי המשפט שהוכחנו,
) ולכן לפי המשפט שהוכחנו, 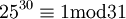 ומכאן
ומכאן 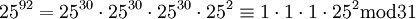 . קל לחשב ש-
. קל לחשב ש- 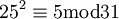 ולכן קיבלנו את המשוואה:
ולכן קיבלנו את המשוואה: 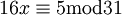 . עוד נראה ש-
. עוד נראה ש- 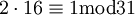 ולכן
ולכן 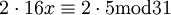 ומכאן ש-
ומכאן ש-