אלגברה מופשטת 1- מועד א' קיץ תשע"ג
תוכן עניינים
שאלה 2
סעיף א'
הוכח את משפט אוילר על החזקות ופתור את המשוואה 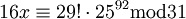
פתרון
משפט אוילר על החזקות אומר שאם 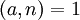 אז
אז 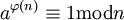 . אבל אם
. אבל אם 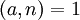 אז לפי משפט,
אז לפי משפט, 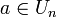 . אחת התוצאות של משפט לגרנז' אומרת שאם מעלים איבר בחזקת סדר של החבורה, נקבל את הנטרלי של החבורה. במקרה הזה, הנטרלי הוא 1 והסדר של החבורה הוא
. אחת התוצאות של משפט לגרנז' אומרת שאם מעלים איבר בחזקת סדר של החבורה, נקבל את הנטרלי של החבורה. במקרה הזה, הנטרלי הוא 1 והסדר של החבורה הוא 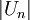 . נזכור שההגדרה של
. נזכור שההגדרה של 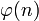 היא בעצם
היא בעצם 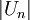 ולכן קיבלנו
ולכן קיבלנו 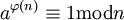 .
.
כעת נפתור את המשוואה. כיוון ש- 31 ראשוני, אז לפי משפט וילסון, 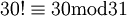 וכיוון ש-30 הפיך ב-
וכיוון ש-30 הפיך ב- 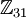 אפשר להסיק ש-
אפשר להסיק ש- 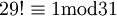 . קיבלנו:
. קיבלנו: 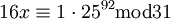 .
.
נזכור ש- 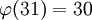 (אם p ראשוני אז
(אם p ראשוני אז 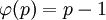 ) ולכן לפי המשפט שהוכחנו,
) ולכן לפי המשפט שהוכחנו, 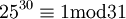 ומכאן
ומכאן 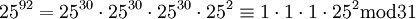 . קל לחשב ש-
. קל לחשב ש- 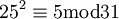 ולכן קיבלנו את המשוואה:
ולכן קיבלנו את המשוואה: 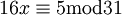 . עוד נראה ש-
. עוד נראה ש- 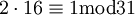 ולכן
ולכן 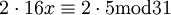 ומכאן ש-
ומכאן ש- 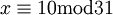
סעיף ב'
האם קיים מונומורפיזם 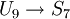 ?
?
אינטואיציה ראשונית לפתרון
נשים לב ש- 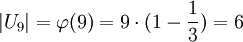 . לכן, לפי משפט מהתרגול, יש 2 אפשרויות:
. לכן, לפי משפט מהתרגול, יש 2 אפשרויות: 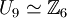 או
או 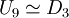 . כיוון ש-
. כיוון ש- 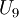 אבלית ו-
אבלית ו- 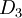 לא, נקבל כי
לא, נקבל כי 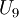 ציקלית. לכן, צריך להתקיים שאם יש מונו' מ-
ציקלית. לכן, צריך להתקיים שאם יש מונו' מ- 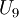 ל-
ל- 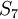 , אזי
, אזי 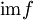 ציקלית והסדר שלה הוא 6 (כיוון שהיא תהיה איזומורפית ל-
ציקלית והסדר שלה הוא 6 (כיוון שהיא תהיה איזומורפית ל- 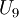 ). לכן, מטרתנו היא למצוא איבר מסדר 6 ב-
). לכן, מטרתנו היא למצוא איבר מסדר 6 ב- 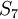 ולשלוח את אחד מהיוצרים של
ולשלוח את אחד מהיוצרים של 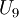 לאותו איבר וזה יתן לנו את הפתרון.
לאותו איבר וזה יתן לנו את הפתרון.
פתרון
נשלח את 2 (קל לראות שהוא אחד מהיוצרים של 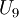 ) לתמורה
) לתמורה 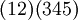 . זוהי תמורה מסדר 6 ולכן סיימנו.
. זוהי תמורה מסדר 6 ולכן סיימנו.
סעיך ג'
הוכיחו: בחבורת מנה 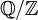 הסדר של כל איבר הוא סופי, אבל החבורה אינה נוצרת סופית.
הסדר של כל איבר הוא סופי, אבל החבורה אינה נוצרת סופית.
פתרון
כל איבר בחבורת המנה הוא מהצורה 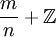 ולכן נראה כי
ולכן נראה כי 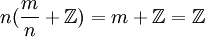 ולכן הסדר של האיבר קטן מ-n, בפרט סופי.
ולכן הסדר של האיבר קטן מ-n, בפרט סופי.
קל לראות ש- 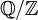 איזומורפית לקבוצת הרציונאלים בין 0 ל-1 (לא כולל 1). הוכחנו בתרגול ובבוחן ש-
איזומורפית לקבוצת הרציונאלים בין 0 ל-1 (לא כולל 1). הוכחנו בתרגול ובבוחן ש-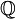 לא נוצרת סופית, נשתמש באותה הוכחה להוכיח שקבוצת הרציונאלים בין 0 ל-1 לא נוצרת סופית
לא נוצרת סופית, נשתמש באותה הוכחה להוכיח שקבוצת הרציונאלים בין 0 ל-1 לא נוצרת סופית