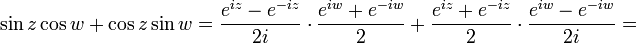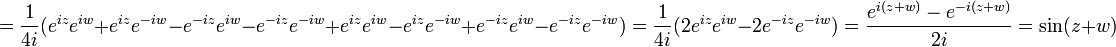הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 6"
מתוך Math-Wiki
(←טריגו) |
(←טריגו) |
||
| שורה 34: | שורה 34: | ||
<math>=\frac{e^{-1}(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)-e(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)}{2i}=\frac{\frac{\sqrt{2}}{2}(\frac{1}{e}-e)+\frac{\sqrt{2}}{2}(\frac{1}{e}+e)i}{2i}=\frac{\sqrt{2}}{4}(\frac{1}{e}+e)-\frac{\sqrt{2}}{4}(\frac{1}{e}-e)i</math> | <math>=\frac{e^{-1}(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)-e(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)}{2i}=\frac{\frac{\sqrt{2}}{2}(\frac{1}{e}-e)+\frac{\sqrt{2}}{2}(\frac{1}{e}+e)i}{2i}=\frac{\sqrt{2}}{4}(\frac{1}{e}+e)-\frac{\sqrt{2}}{4}(\frac{1}{e}-e)i</math> | ||
| + | |||
| + | ====תרגיל==== | ||
| + | הוכיחו: <math>\sin(z+w)=\sin z\cos w+\cos z\sin w</math>. | ||
| + | |||
| + | ====פתרון===== | ||
| + | נפתח את צד ימין: | ||
| + | |||
| + | <math>\sin z\cos w+\cos z\sin w=\frac{e^{iz}-e^{-iz}}{2i}\cdot \frac{e^{iw}+e^{-iw}}{2}+\frac{e^{iz}+e^{-iz}}{2}\cdot \frac{e^{iw}-e^{-iw}}{2i}=</math> | ||
| + | |||
| + | <math>=\frac{1}{4i}(e^{iz}e^{iw}+e^{iz}e^{-iw}-e^{-iz}e^{iw}-e^{-iz}e^{-iw}+e^{iz}e^{iw}-e^{iz}e^{-iw}+e^{-iz}e^{iw}-e^{-iz}e^{-iw})=\frac{1}{4i}(2e^{iz}e^{iw}-2e^{-iz}e^{-iw})=\frac{e^{i(z+w)}-e^{-i(z+w)}}{2i}=\sin (z+w)</math> | ||
גרסה מ־10:51, 11 בדצמבר 2018
חזרה ל מערכי תרגול.
תוכן עניינים
אקסופנט
ראינו בשבוע שעבר שהפונקציה 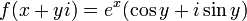 גזירה ומקיימת
גזירה ומקיימת 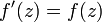 , וראיתם בהרצאה שהיא מקיימת את כל התכונות הנדרשות לפונקציית האקספוננט, ולכן הגדרנו:
, וראיתם בהרצאה שהיא מקיימת את כל התכונות הנדרשות לפונקציית האקספוננט, ולכן הגדרנו: 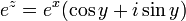 .
.
לדוגמא, נחשב 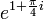 :
:
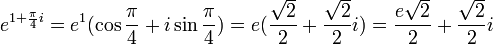 .
.
תרגיל
כידוע, בממשיים מתקיים 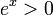 . מה לגבי המרוכבים? האם קיים
. מה לגבי המרוכבים? האם קיים 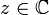 כך ש
כך ש 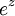 הוא ממשי וקטן מאפס?
הוא ממשי וקטן מאפס?
פתרון
כן! נתחיל מדוגמא, ואז נבין את הפתרון הכללי. נחפש 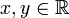 כך ש
כך ש 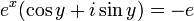 .
.
ראשית, כדי שהתוצאה תהיה ממשית דרוש 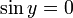 , ולכן
, ולכן 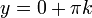 . כעת נקבל
. כעת נקבל 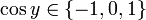 , וכיון שאנחנו רוצים לקבל מספר שלילי נרצה
, וכיון שאנחנו רוצים לקבל מספר שלילי נרצה 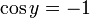 , ולכן ניקח
, ולכן ניקח 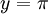 .
.
מה שקיבלנו עד כה זה 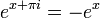 , ולכן אם ניקח
, ולכן אם ניקח 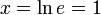 נקבל
נקבל 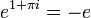 כדרוש.
כדרוש.
באופן כללי: יהי 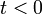 ממשי. נבחר
ממשי. נבחר 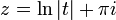 ונקבל
ונקבל 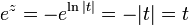 .
.
תרגיל
הוכיחו שמתקיים: 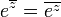
פתרון
לפי הגדרה: 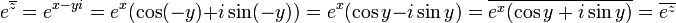 .
.
טריגו
הגדרתם בהרצאה את הפונקציות הטריגונומטריות 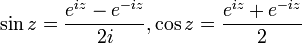 .
.
לדוגמא, נחשב:
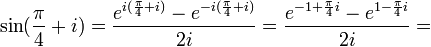
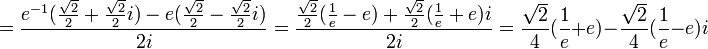
תרגיל
הוכיחו: 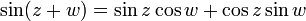 .
.
פתרון=
נפתח את צד ימין: