אנליזה מתקדמת למורים תרגול 6

חזרה ל מערכי תרגול.

אקסופנט

ראינו בשבוע שעבר שהפונקציה 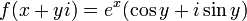$f(x+yi)=e^x(\cos y+i\sin y)$ גזירה ומקיימת 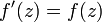$f'(z)=f(z)$, וראיתם בהרצאה שהיא מקיימת את כל התכונות הנדרשות לפונקציית האקספוננט, ולכן הגדרנו: $e^z=e^x(\cos y+i\sin y)$.

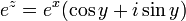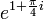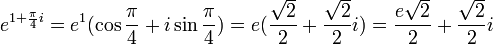לדוגמא, נחשב $e^{1+\frac{\pi}{4}i}$:

$e^{1+\frac{\pi}{4}i}=e^1(\cos \frac{\pi}{4} +i\sin \frac{\pi}{4})=e(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)=\frac{e\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$.

תרגיל

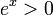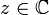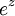כידוע, בממשיים מתקיים $e^x>0$. מה לגבי המרוכבים? האם קיים $z\in \mathbb{C}$ כך ש $e^z$ הוא ממשי וקטן מאפס?

פתרון

כן! נתחיל מדוגמא, ואז נבין את הפתרון הכללי. נחפש 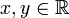$x,y\in \mathbb{R}$ כך ש $e^x(\cos y+i\sin y)=-e$.

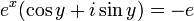ראשית, כדי שהתוצאה תהיה ממשית דרוש 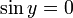$\sin y=0$, ולכן 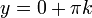$y=0+\pi k$. כעת נקבל 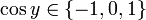$\cos y\in \{-1,0,1\}$, וכיון שאנחנו רוצים לקבל מספר שלילי נרצה 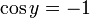$\cos y=-1$, ולכן ניקח $y=\pi$.

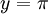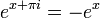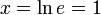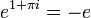מה שקיבלנו עד כה זה $e^{x+\pi i}=-e^x$, ולכן אם ניקח $x=\ln e=1$ נקבל $e^{1+\pi i}=-e$ כדרוש.

באופן כללי: יהי 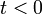$t<0$ ממשי. נבחר 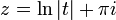$z=\ln |t|+\pi i$ ונקבל $e^z=-e^{\ln |t|}=-|t|=t$.

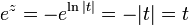תרגיל

הוכיחו שמתקיים: 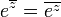$e^{\overline{z}}=\overline{e^z}$

פתרון

לפי הגדרה: 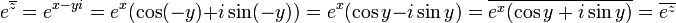$e^{\overline{z}}=e^{x-yi}=e^x(\cos(-y)+i\sin(-y))=e^x(\cos y-i\sin y)=\overline{e^x(\cos y+i\sin y)}=\overline{e^z}$.

טריגו

הגדרתם בהרצאה את הפונקציות הטריגונומטריות 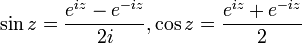$\sin z=\frac{e^{iz}-e^{-iz}}{2i},\cos z=\frac{e^{iz}+e^{-iz}}{2}$.

לדוגמא, נחשב:

$\sin(\frac{\pi}{4}+i)=\frac{e^{i(\frac{\pi}{4}+i)}-e^{-i(\frac{\pi}{4}+i)}}{2i}=\frac{e^{-1+\frac{\pi}{4}i}-e^{1-\frac{\pi}{4}i}}{2i}=$

$=\frac{e^{-1}(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)-e(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)}{2i}=\frac{\frac{\sqrt{2}}{2}(\frac{1}{e}-e)+\frac{\sqrt{2}}{2}(\frac{1}{e}+e)i}{2i}=\frac{\sqrt{2}}{4}(\frac{1}{e}+e)-\frac{\sqrt{2}}{4}(\frac{1}{e}-e)i$

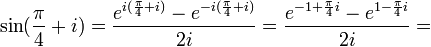
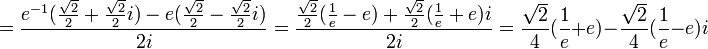
תרגיל

הוכיחו: 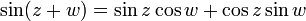$\sin(z+w)=\sin z\cos w+\cos z\sin w$.

פתרון=

נפתח את צד ימין:

$\sin z\cos w+\cos z\sin w=\frac{e^{iz}-e^{-iz}}{2i}\cdot \frac{e^{iw}+e^{-iw}}{2}+\frac{e^{iz}+e^{-iz}}{2}\cdot \frac{e^{iw}-e^{-iw}}{2i}=$

$=\frac{1}{4i}(e^{iz}e^{iw}+e^{iz}e^{-iw}-e^{-iz}e^{iw}-e^{-iz}e^{-iw}+e^{iz}e^{iw}-e^{iz}e^{-iw}+e^{-iz}e^{iw}-e^{-iz}e^{-iw})=\frac{1}{4i}(2e^{iz}e^{iw}-2e^{-iz}e^{-iw})=\frac{e^{i(z+w)}-e^{-i(z+w)}}{2i}=\sin (z+w)$

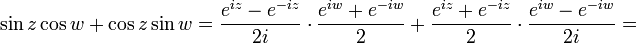
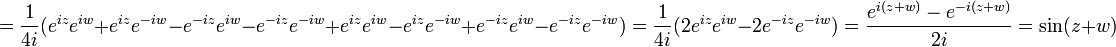
לוגריתם

אנחנו רוצים פונקציה הופכית לאקספוננט. הבעיה היא, שפונקציית האקספונט לא חח"ע. מה עושים? שמים לב שבתחום 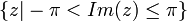$\{z|-\pi<Im(z)\leq \pi\}$ היא כן חח"ע, מגדירים שם את ההופכית, וקורים לה $\log$.

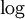הגדרה מפורשת

$\log(z)=\ln |z|+iarg(z)$

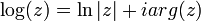
לדוגמא: 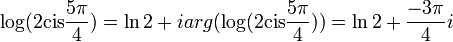$\log(2\text{cis}\frac{5\pi}{4})=\ln 2+iarg(\log(2\text{cis}\frac{5\pi}{4}))=\ln 2+\frac{-3\pi}{4}i$.

תרגיל

הוכיחו שלכל מספר מרוכב 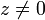$z\neq 0$ שאיננו ממשי שלילי מתקיים: $\log(\overline{z})=\overline{\log(z)}$.

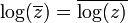פתרון

נשתמש בעובדה מהעבר: 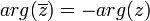$arg(\overline{z})=-arg(z)$ (אתם זוכרים שכשדיברנו על cis אמרנו שבצמוד לוקחים את מינוס הזוית? וכמובן אם הזוית המקורית נמצאת בין מינוס פאי לפאי, אז גם המינוס שלה, וכאן משתמשים בהנחה שהוא לא שלילי). לכן:

$\log(\overline{z})=\ln |\overline{z}|+iarg(\overline{z})=\ln |z|-iarg(z)=\overline{\ln |z|+iarg(z)}=\overline{\log(z)}$

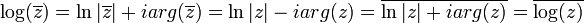
חזקות

בממשיים מגדירים: 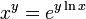$x^y=e^{y\ln x}$. אז נעשה זאת גם כאן: $z^w=e^{w\log z}$.

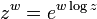לדוגמא: 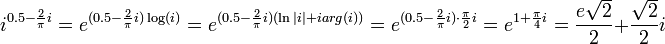$i^{0.5-\frac{2}{\pi}i}=e^{(0.5-\frac{2}{\pi}i)\log(i)}=e^{(0.5-\frac{2}{\pi}i)(\ln|i|+iarg(i))}=e^{(0.5-\frac{2}{\pi}i)\cdot \frac{\pi}{2}i}=e^{1+\frac{\pi}{4}i}=\frac{e\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$

ענפים שונים

כאמור, ההגדרות של לוגריתם וחזקה תלויות בבחירת הענף, כלומר, טווח הזוית המגדירה מס' מרוכב. הענף הראשי הוא 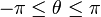$-\pi \leq \theta \leq \pi$. אך ניתן לבחור גם ענפים אחרים כמו 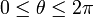$0\leq \theta \leq 2\pi$, ולקבל הגדרה שונה ללוגריתם וחזקה.

תרגיל

נתבונן בענף 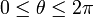$0\leq \theta \leq 2\pi$ ונחשב את $L(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i),-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i^i$