הבדלים בין גרסאות בדף "הלמה של צורן"

גרסה מ־00:56, 10 במאי 2015

הלמה של צורן היא למה יסודית במתמטיקה, השקולה לאקסיומת הבחירה. הלמה מספקת הוכחה לקיומם של אובייקטים מתמטיים שקשה (ולפעמים אי אפשר) לבנות באופן ישיר.

תוכן עניינים

1 מבוא
- 1.1 אקסיומת הבחירה
2 הלמה של צורן
3 שימושים

מבוא

את כל המשפטים במתמטיקה אפשר, עקרונית, להוכיח באופן פורמלי ממערכת אקסיומות אחת. האקסיומות האלה, המתארות את תורת הקבוצות, נקראות "אקסיומות צרמלו-פרנקל" (על-שם המתמטיקאים שניסחו אותן). רוב האקסיומות פשוטות בתכלית: קיימת קבוצה ריקה, לכל קבוצה יש קבוצת חזקה, וכדומה. רק אקסיומה אחת ברשימה טוענת טענה שאפשר לא לקבל אינטואיטיבית. לאקסיומה זו, הקרויה אקסיומת הבחירה, יש גרסאות שקולות רבות, שהלמה של צורן היא אחת מהן (את השקילות אפשר להוכיח משאר האקסיומות).

אקסיומת הבחירה

((ניסוח, הסבר))

הלמה של צורן

ניסוח

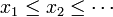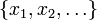תהי X קבוצה סדורה (קבוצה עם יחס סדר חלקי חלש). תת-קבוצה של X הסדורה לינארית נקראת שרשרת (לדוגמא, אם $x_1\leq x_2 \leq \cdots$ אז $\{x_1,x_2,\dots\}$ היא שרשרת, שבה לכל איבר יש עוקב ישיר; אבל זהו בשום אופן אינו המקרה הכללי: המספרים הרציונליים מהווים שרשרת שבה אין לאף איבר עוקב ישיר, ויש כמובן גם שרשראות שאינן בנות מניה).

הלמה של צורן. תהי X קבוצה לא ריקה. נניח שלכל שרשרת ב-X יש חסם מלעיל. אז יש ל-X איבר מקסימלי.

הערה 1. הטענה כמובן אינה נכונה אם X ריקה. זו אינה נקודה שולית: הלמה של צורן מספקת הוכחת קיום, וכדי להפעיל אותה יש לוודא שקיים איזשהו איבר בקבוצה X; רק אחר-כך מספקת הלמה איבר מקסימלי בקבוצה.

הערה 2. אם X עצמה סדורה לינארית, זוהי טענה טריוויאלית (משום שאם X שרשרת, יש לה חסם מלעיל לפי ההנחה, והוא איבר מקסימלי). מובן מאליו שהלמה נועדה לטפל במקרים שבהם הסדר של X אינו לינארי.

(("הוכחה" אינטואיטיבית, והסבר מדוע זה אינו מספיק))

הוכחת הלמה של צורן מאקסיומת הבחירה

((הוכחה))

הלמה של צורן עבור משפחה של קבוצות

כדי להפעיל את הלמה של צורן יש להראות שלכל שרשרת יש חסם מלעיל. אם X היא משפחה של קבוצות, זה עשוי להיות קל במיוחד. אנו אומרים ש-X סגורה לאיחוד של שרשראות אם לכל שרשרת 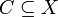$\ C \subseteq X$ , האיחוד 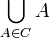$\ \bigcup_{A \in C} A$ שייך ל-X. (שוב, אם X היתה סדורה לינארית, אפשר היה לקחת את האיחוד של כל הקבוצות ב-X; אלא שבכל המקרים המעניינים, X אינה לינארית, ואפילו אינה סגורה ביחס לאיחוד סופי של סתם שני אברים).

הלמה של צורן עבור משפחה של קבוצות. תהי X משפחה לא ריקה של קבוצות, הסגורה לאיחוד של שרשראות. אז יש ל-X איבר מקסימלי.

שימושים

ללמה של צורן שימושים רבים בכל תחומי המתמטיקה. נדגים כמה מהם. הקורא מוזמן להתמקד באלו העוסקות בתחומים המוכרים לו, ויכול לדלג ללא חשש.

לכל מרחב וקטורי יש בסיס

משפט. לכל מרחב וקטורי יש בסיס.

זו טענה שאפשר להוכיח באינדוקציה אם יש למרחב בסיס סופי, אבל המקרה הכללי דורש כלים מתקדמים יותר.

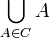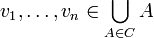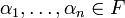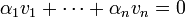הוכחה. יהי V מרחב וקטורי מעל שדה F. נסמן ב-X את משפחת תת-הקבוצות של V שאינן תלויות לינארית (הקבוצה הריקה שייכת ל-X, ולכן X אינה ריקה). נוכיח ש-X סגורה לאיחוד של שרשראות. אכן, תהי C שרשרת ב-X. נתבונן באיחוד $\ \bigcup_{A \in C} A$ . יהיו $\ v_1,\dots,v_n \in \bigcup_{A \in C} A$ אברים של המרחב, כך שקיימים סקלרים $\ \alpha_1,\dots,\alpha_n \in F$ כך ש- $\ \alpha_1v_1+\cdots+\alpha_nv_n = 0$ . 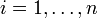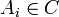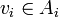לכל $\ i=1,\dots,n$ יש איבר $\ A_i \in C$ כך ש- $\ v_i \in A_i$ ; אבל C היא שרשרת, ולכן מבין האברים 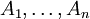$\ A_1,\dots,A_n$ יש אחד המכיל את כולם; נאמר שזהו 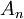$\ A_n$ . 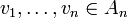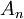אז $\ v_1,\dots,v_n \in A_n$ , אבל $\ A_n$ בלתי תלויה לינארית (משום שהיא שייכת ל-X), ולכן המקדמים 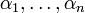$\ \alpha_1,\dots,\alpha_n$ שווים כולם לאפס.

לפי הלמה של צורן, יש ב-X קבוצה מקסימלית, שנסמן ב-B. היא בלתי-תלויה לינארית (משום שכל הקבוצות ב-X כאלה). נשאר להראות שהיא פורשת את המרחב V. יהי 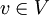$\ v\in V$ . אם הוקטור v אינו נפרש על-ידי B, אז הקבוצה 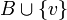$\ B \cup \{v\}$ בלתי-תלויה לינארית, וזו סתירה למקסימליות של B. לכן כל וקטור נפרש על-ידי B, ומכאן ש-B בסיס.

בכל חוג יש אידאל מקסימלי

משפט. בכל חוג עם יחידה יש אידאל (אמיתי) מקסימלי.

תת-קבוצה של חוג R נקראת אידיאל אם היא סגורה לחיבור וחיסור, וכן לכפל מימין ומשמאל באברים של R. אידיאל הוא "אמיתי" אם הוא אינו שווה לכל החוג. אידיאל (אמיתי) הוא מקסימלי אם אינו מוכל (ממש) בשום אידיאל (אמיתי) אחר. המפתח להוכחה הוא העובדה שאידיאל אמיתי אינו יכול להכיל את איבר היחידה (אחרת הוא כולל כל איבר לפי הסגירות לכפל באברי החוג).

הוכחה. נסמן ב-X את קבוצת האידיאלים האמיתיים של R (אידיאל האפס נמצא שם, ולכן X לא ריקה). איחוד על שרשרת של אידיאלים סגור בוודאי לחיבור וחיסור ולכפל באברי החוג, ולכן הוא אידיאל. מכיוון שכל האברים בשרשרת אינם כוללים את איבר היחידה, גם האיחוד שלהם אינו כולל את איבר היחידה, ולכן הוא אידיאל אמיתי. לפי הלמה של צורן, יש ב-X איבר מקסימלי, וזהו אידיאל אמיתי מקסימלי.

הערה. אותה הוכחה בדיוק מראה שכל אידיאל I של R מוכל באידיאל מקסימלי; קח X להיות קבוצת האידיאלים האמיתיים המכילים את I. ההוכחה אינה עובדת בחוגים ללא יחידה, ואכן הטענה אינה נכונה עבורם.

תרגיל. בכל חוג עם יחידה יש אידיאל שמאלי מקסימלי. (מסקנה: לכל חוג עם יחידה יש מודולים פשוטים).

תרגיל. יהי S מונויד כפלי בחוג R, שאינו כולל את 0. הראה שיש אידיאל שהוא מקסימלי בין אלו שאינם חותכים את S. (כל אידיאל כזה הוא "אידיאל ראשוני").

תרגיל. לכל מודול נוצר סופית יש תת-מודול (אמיתי) מקסימלי.

לכל שדה יש סגור אלגברי

שדה E הוא סגור אלגברית אם לכל פולינום עם מקדמים ב-E יש שורש ב-E (לדוגמא, שדה המספרים המרוכבים סגור אלגברית). שדה E הוא סגור אלגברי של שדה F, אם E סגור אלגברית, וההרחבה E/F אלגברית.

משפט. לכל שדה F יש סגור אלגברי.

ההוכחה מתחילה באידיאל הנוצר על-ידי הצבות של משתנים פורמליים בכל הפולינומים (המתוקנים) מעל השדה. כפי שראינו לעיל (בעזרת הלמה של צורן), האידיאל הזה מוכל באידיאל מקסימלי, וחוג המנה (של כל חוג קומוטטיבי מעל אידיאל מקסימלי) הוא שדה. לפרטים, ראה כאן, סעיף 4.1.5 בעמ' 65.

הסגור האלגברי יחיד עד-כדי איזומורפיזם

משפט. כל שני סגורים אלגבריים של אותו שדה F, הם איזומורפיים (כהרחבות של F).

יהיו E_1, E_2 שני סגורים אלגבריים של F. הפעם מבוססת ההוכחה על משפחת השיכונים של תת-שדות של E_1 בתוך E_2. גם כאן, השיכון ה"מקסימלי" (מושג שיש להגדיר, כמובן) מהווה שיכון מלא של E_1 לתוך E_2; אבל אז E_2 הוא הרחבה אלגברית של השדה E_1, שהוא סגור אלגברית, ולכן השיכון הוא על. ראה כאן, סעיף 4.1.6, עמ' 66 לפרטים.

התשתית של מודול היא סכום ישר של תת-מודולים פשוטים

יהי M מודול מעל חוג R. התשתית שלו, אותה מסמנים ב-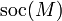 $\ \operatorname{soc}(M)$ , היא הסכום של כל תת-המודולים הפשוטים של M.

משפט. 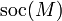$\ \operatorname{soc}(M)$ הוא סכום ישר של תת-מודולים פשוטים של M (בדרך כלל לא כולם).

הוכחה. נסמן ב-X את המשפחות של תת-מודולים פשוטים שהסכום שלהם הוא ישר (המשפחה הריקה היא כזו, ולכן X לא ריקה). X סגור לאיחוד של שרשראות (ההוכחה דומה לזו של קיום הבסיס למרחב וקטורי). לכן יש ב-X משפחה מקסימלית, שנסמן ב-S. אם קיים תת-מודול פשוט שאינו מוכל בסכום שלה, אז צירופו למשפחה נותן משפחה בלתי-תלויה גדולה יותר, בסתירה למקסימליות. לכן כל תת-מודול פשוט מוכל בסכום של אברי S; מכן שהסכום הזה (שהוא סכום ישר כי S שייכת ל-X) שווה ל-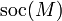 $\ \operatorname{soc}(M)$ .

הערה. המשפט על קיום בסיס למרחב וקטורי הוא מקרה פרטי: אם M הוא מרחב וקטורי מעל השדה F, כל תת-מרחב חד-ממדי הוא פשוט, ולכן M שווה לתשתית של עצמו. לפי המשפט M הוא סכום ישר של תת-מרחבים חד-ממדיים, כלומר יש לו בסיס.

@@ שורה 31: / שורה 31: @@
 כדי להפעיל את הלמה של צורן יש להראות שלכל שרשרת יש חסם מלעיל. אם X היא משפחה של קבוצות, זה עשוי להיות קל במיוחד. אנו אומרים ש-X סגורה לאיחוד של שרשראות אם לכל שרשרת <math>\ C \subseteq X</math>, האיחוד <math>\ \bigcup_{A \in C} A</math> שייך ל-X. (שוב, אם X היתה סדורה לינארית, אפשר היה לקחת את האיחוד של כל הקבוצות ב-X; אלא שבכל המקרים המעניינים, X אינה לינארית, ואפילו אינה סגורה ביחס לאיחוד סופי של סתם שני אברים).
-* (הלמה של צורן עבור משפחה של קבוצות) תהי X משפחה של קבוצות, הסגורה לאיחוד של שרשראות. אז יש ל-X איבר מקסימלי.
+'''הלמה של צורן עבור משפחה של קבוצות'''. תהי X משפחה לא ריקה של קבוצות, הסגורה לאיחוד של שרשראות. אז יש ל-X איבר מקסימלי.
 == שימושים ==

הבדלים בין גרסאות בדף "הלמה של צורן"

גרסה מ־00:56, 10 במאי 2015

תוכן עניינים

מבוא

אקסיומת הבחירה

הלמה של צורן

ניסוח

הוכחת הלמה של צורן מאקסיומת הבחירה

הלמה של צורן עבור משפחה של קבוצות

שימושים

לכל מרחב וקטורי יש בסיס

בכל חוג יש אידאל מקסימלי

לכל שדה יש סגור אלגברי

הסגור האלגברי יחיד עד-כדי איזומורפיזם

התשתית של מודול היא סכום ישר של תת-מודולים פשוטים

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים