הבדלים בין גרסאות בדף "חוג ריבועי"
(יצירת דף עם התוכן "'''חוג ריבועי''' הוא חוג שבו כל איבר מקיים משוואה ממעלה שניה מעל השלמים. עבור שלם D חופשי מ...") |
(←חישוב חוגי מנה) |
||
| (5 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
'''חוג ריבועי''' הוא חוג שבו כל איבר מקיים משוואה ממעלה שניה מעל השלמים. | '''חוג ריבועי''' הוא חוג שבו כל איבר מקיים משוואה ממעלה שניה מעל השלמים. | ||
| − | עבור שלם D [[חופשי מריבועים]] (כלומר שאין לו מחלק ריבועי), נסמן <math>\ {\mathcal{O}}_D = \begin{cases}\mathbb{Z}[\sqrt{D}] & D \equiv | + | עבור שלם D [[חופשי מריבועים]] (כלומר שאין לו מחלק ריבועי), נסמן <math>\ {\mathcal{O}}_D = \begin{cases}\mathbb{Z}[\sqrt{D}] & D \equiv 2,3 \pmod{4} \\ |
| − | \mathbb{Z}[\frac{1+\sqrt{D}}{2}] & D \equiv | + | \mathbb{Z}[\frac{1+\sqrt{D}}{2}] & D \equiv 1 \pmod{4} \end{cases}</math>. החוג <math>\ \mathcal{O}_D</math> הוא "הסגור השלם" של חוג השלמים בשדה <math>\ \mathbb{Q}[\sqrt{D}]</math>. כל תחום שלמות ריבועי הוא תת-חוג של חוג מהצורה הזו. |
| + | |||
| + | תחומי שלמות ריבועיים הם "מעבדה" לבחינת מושגי היסוד של תחומי שלמות: איברים ראשוניים ואי-פריקים, פריקות יחידה ואידיאלים ראשיים, אוקלידיות וכדומה. חלק מהמושגים האלה דורשים חישוב של חוגי מנה. נדגים זאת בכמה מקרים. | ||
| + | |||
| + | === חישוב חוגי מנה === | ||
| + | נחשב את <math>\ \mathbb{Z}[\sqrt{10}]/\langle 4-\sqrt{10}\rangle</math>. כדי לוודא שלא תשתחל פנימה טעות בסימן של השורש, נחליף אותו בשם משתנה ונכתוב את החוג המקורי כמנה <math>\ \mathbb{Z}[t]/\langle t^2-10\rangle</math>, ואת חוג המנה המבוקש כמנה <math>\ \mathbb{Z}[t]/\langle t^2-10, 4-t\rangle</math>. מכיוון שבחוג המנה הזה t=4, מתברר ש-<math>0 \equiv t^2-10 \equiv 4^2-10 = -6</math>, כלומר המנה היא <math>\ \mathbb{Z}_6[t]/\langle t^2-10, 4-t\rangle = \mathbb{Z}_6</math>. | ||
| + | |||
| + | נחשב את המנה <math>\ \mathbb{Z}[\frac{1+\sqrt{-11}}{2}]/\langle \frac{13+7\sqrt{-11}}{2}\rangle</math>. כאן חשוב עוד יותר להחליף שמות ולסמן <math>\ x = \frac{1+\sqrt{-11}}{2}</math>, כאשר <math>\ x^2-x+3=0</math>. מכיוון ש-<math>\ \frac{13+7\sqrt{-11}}{2} = 3+7x</math>, אנחנו מחשבים את המנה | ||
| + | <math>\ \mathbb{Z}[x]/\langle x^2-x+3, \ 3+7x\rangle</math>. הנורמה של 3+7x היא 177=3*59, ומכיוון שהנורמה היא (כמובן) כפולה של 3+7x, האידיאל מכיל את 177. זה אומר שהמנה שווה ל-<math>\ \mathbb{Z}_{177}[x]/\langle x^2-x+3,\ 3+7x\rangle</math>! בחוג הזה 7 הוא הפיך, ואפשר לפתור את המשוואה: <math>\ 0 \equiv 76(3+7x) = 51+x</math>, כלומר x=-51. הצבת ערך זה מאפסת (שלא במפתיע) את התנאי הריבועי, ולכן חוג המנה הוא <math>\ \mathbb{Z}_{177} \cong \mathbb{Z}_3 \times \mathbb{Z}_{59}</math>. | ||
גרסה אחרונה מ־08:32, 4 ביולי 2019
חוג ריבועי הוא חוג שבו כל איבר מקיים משוואה ממעלה שניה מעל השלמים.
עבור שלם D חופשי מריבועים (כלומר שאין לו מחלק ריבועי), נסמן ![\ {\mathcal{O}}_D = \begin{cases}\mathbb{Z}[\sqrt{D}] & D \equiv 2,3 \pmod{4} \\
\mathbb{Z}[\frac{1+\sqrt{D}}{2}] & D \equiv 1 \pmod{4} \end{cases}](/images/math/e/d/c/edccd7fd7d855362cb10cfb4cf7c12a5.png) . החוג
. החוג 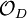 הוא "הסגור השלם" של חוג השלמים בשדה
הוא "הסגור השלם" של חוג השלמים בשדה ![\ \mathbb{Q}[\sqrt{D}]](/images/math/4/d/d/4dd5f6ad354c1042e095db253ca41544.png) . כל תחום שלמות ריבועי הוא תת-חוג של חוג מהצורה הזו.
. כל תחום שלמות ריבועי הוא תת-חוג של חוג מהצורה הזו.
תחומי שלמות ריבועיים הם "מעבדה" לבחינת מושגי היסוד של תחומי שלמות: איברים ראשוניים ואי-פריקים, פריקות יחידה ואידיאלים ראשיים, אוקלידיות וכדומה. חלק מהמושגים האלה דורשים חישוב של חוגי מנה. נדגים זאת בכמה מקרים.
חישוב חוגי מנה
נחשב את ![\ \mathbb{Z}[\sqrt{10}]/\langle 4-\sqrt{10}\rangle](/images/math/c/6/3/c638333b776a0e96c74230a845086afe.png) . כדי לוודא שלא תשתחל פנימה טעות בסימן של השורש, נחליף אותו בשם משתנה ונכתוב את החוג המקורי כמנה
. כדי לוודא שלא תשתחל פנימה טעות בסימן של השורש, נחליף אותו בשם משתנה ונכתוב את החוג המקורי כמנה ![\ \mathbb{Z}[t]/\langle t^2-10\rangle](/images/math/9/f/e/9fecbcb324dd745a3bce0adaf504e3e2.png) , ואת חוג המנה המבוקש כמנה
, ואת חוג המנה המבוקש כמנה ![\ \mathbb{Z}[t]/\langle t^2-10, 4-t\rangle](/images/math/2/7/e/27e90a9a1546fafc527c0604bd624ca8.png) . מכיוון שבחוג המנה הזה t=4, מתברר ש-
. מכיוון שבחוג המנה הזה t=4, מתברר ש-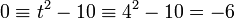 , כלומר המנה היא
, כלומר המנה היא ![\ \mathbb{Z}_6[t]/\langle t^2-10, 4-t\rangle = \mathbb{Z}_6](/images/math/1/3/f/13f74f96b3f0eae7c3e8718be6c9a281.png) .
.
נחשב את המנה ![\ \mathbb{Z}[\frac{1+\sqrt{-11}}{2}]/\langle \frac{13+7\sqrt{-11}}{2}\rangle](/images/math/6/c/2/6c2d8a4eaf0e7954d8eedc795fc7e376.png) . כאן חשוב עוד יותר להחליף שמות ולסמן
. כאן חשוב עוד יותר להחליף שמות ולסמן 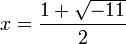 , כאשר
, כאשר 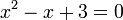 . מכיוון ש-
. מכיוון ש-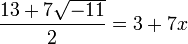 , אנחנו מחשבים את המנה
, אנחנו מחשבים את המנה
![\ \mathbb{Z}[x]/\langle x^2-x+3, \ 3+7x\rangle](/images/math/6/4/7/647a6b31050f491e82907ae4f429cf01.png) . הנורמה של 3+7x היא 177=3*59, ומכיוון שהנורמה היא (כמובן) כפולה של 3+7x, האידיאל מכיל את 177. זה אומר שהמנה שווה ל-
. הנורמה של 3+7x היא 177=3*59, ומכיוון שהנורמה היא (כמובן) כפולה של 3+7x, האידיאל מכיל את 177. זה אומר שהמנה שווה ל-![\ \mathbb{Z}_{177}[x]/\langle x^2-x+3,\ 3+7x\rangle](/images/math/8/4/6/8469fa93398768a937a471dac8ed9d28.png) ! בחוג הזה 7 הוא הפיך, ואפשר לפתור את המשוואה:
! בחוג הזה 7 הוא הפיך, ואפשר לפתור את המשוואה: 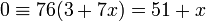 , כלומר x=-51. הצבת ערך זה מאפסת (שלא במפתיע) את התנאי הריבועי, ולכן חוג המנה הוא
, כלומר x=-51. הצבת ערך זה מאפסת (שלא במפתיע) את התנאי הריבועי, ולכן חוג המנה הוא 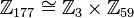 .
.