גרסה מ־18:31, 9 ביולי 2013

תוכן עניינים

1 שאלה 2
- 1.1 סעיף א
- 1.2 סעיף ב
2 שאלה 3
- 2.1 סעיף א
3 שאלה 4
4 שאלה 6

שאלה 2

סעיף א

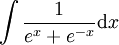
$\int\frac{1}{e^x+e^{-x}}\mathrm{d}x$

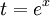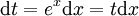
נציב $t=e^x$ ואז $\mathrm{d}t=e^x\mathrm{d}x=t\mathrm{d}x$

לאחר הצבה נקבל

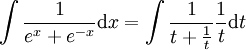
$\int\frac{1}{e^x+e^{-x}}\mathrm{d}x=\int\frac{1}{t+\frac{1}{t}}\frac{1}{t}\mathrm{d}t$

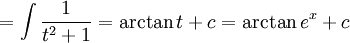
$=\int\frac{1}{t^2+1}=\arctan t+c=\arctan e^x+c$

סעיף ב

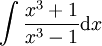
$\int\frac{x^3+1}{x^3-1}\mathrm{d}x$

על ידי חילוק פולינומים קל לראות ש

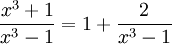
$\frac{x^3+1}{x^3-1}=1+\frac{2}{x^3-1}$

אז נתמקד בחישוב 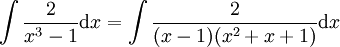$\int\frac{2}{x^3-1}\mathrm{d}x=\int\frac{2}{(x-1)(x^2+x+1)}\mathrm{d}x$

לפי האלגוריתם לחישוב אינטגרל של פונקציה רציונאלית נחפש

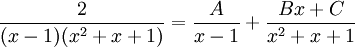
$\frac{2}{(x-1)(x^2+x+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+x+1}$

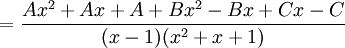
$=\frac{Ax^2+Ax+A+Bx^2-Bx+Cx-C}{(x-1)(x^2+x+1)}$

כלומר קיבלנו מערכת משוואות

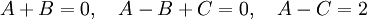
$A+B=0, \quad A-B+C=0,\quad A-C=2$

וקל לראות שהפתרון שלה הוא:

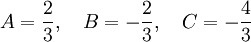
$A=\frac{2}{3},\quad B=-\frac{2}{3},\quad C= -\frac{4}{3}$

ברור ש

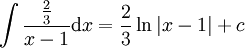
$\int\frac{\frac{2}{3}}{x-1}\mathrm{d}x=\frac{2}{3}\ln|x-1|+c$

נותר לחשב את 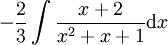$-\frac{2}{3}\int\frac{x+2}{x^2+x+1}\mathrm{d}x$

לפי השלמה לריבוע

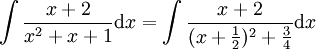
$\int\frac{x+2}{x^2+x+1}\mathrm{d}x=\int\frac{x+2}{(x+\frac{1}{2})^2+\frac{3}{4}}\mathrm{d}x$

נבצע הצבה 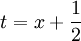$t=x+\frac{1}{2}$ (רק בשביל נוחות) ואז נישאר עם

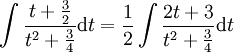
$\int\frac{t+\frac{3}{2}}{t^2+\frac{3}{4}}\mathrm{d}t=\frac{1}{2}\int\frac{2t+3}{t^2+\frac{3}{4}}\mathrm{d}t$

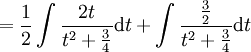
$=\frac{1}{2}\int\frac{2t}{t^2+\frac{3}{4}}\mathrm{d}t+\int\frac{\frac{3}{2}}{t^2+\frac{3}{4}}\mathrm{d}t$

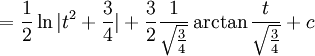
$=\frac{1}{2}\ln|t^2+\frac{3}{4}|+\frac{3}{2}\frac{1}{\sqrt{\frac{3}{4}}}\arctan\frac{t}{\sqrt{\frac{3}{4}}}+c$

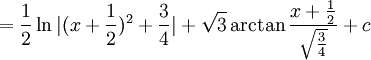
$=\frac{1}{2}\ln|(x+\frac{1}{2})^2+\frac{3}{4}|+\sqrt{3}\arctan\frac{x+\frac{1}{2}}{\sqrt{\frac{3}{4}}}+c$

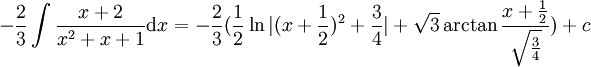
ולכן $-\frac{2}{3}\int\frac{x+2}{x^2+x+1}\mathrm{d}x=-\frac{2}{3}(\frac{1}{2}\ln|(x+\frac{1}{2})^2+\frac{3}{4}|+\sqrt{3}\arctan\frac{x+\frac{1}{2}}{\sqrt{\frac{3}{4}}})+c$

אם נסכום את כל מה שקיבלנו נקבל שהתוצאה היא

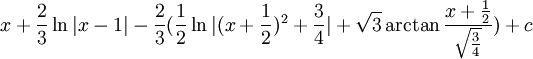
$x+\frac{2}{3}\ln|x-1|-\frac{2}{3}(\frac{1}{2}\ln|(x+\frac{1}{2})^2+\frac{3}{4}|+\sqrt{3}\arctan\frac{x+\frac{1}{2}}{\sqrt{\frac{3}{4}}})+c$

ואם מסדרים את זה יוצא

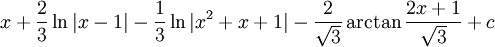
$x+\frac{2}{3}\ln|x-1|-\frac{1}{3}\ln|x^2+x+1|-\frac{2}{\sqrt{3}}\arctan\frac{2x+1}{\sqrt{3}}+c$

שאלה 3

סעיף א

צריך לבדוק אם 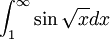$\int_1^\infty \sin\sqrt{x}dx$ מתכנס או מתבדר.

הצעה לפתרון: ננסה לחשב את 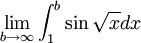$\lim_{b\to\infty} \int_1^b \sin \sqrt{x} dx$ . נסתכל על 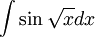$\int \sin\sqrt x dx$ . ע"י החלפת משתנים נקבל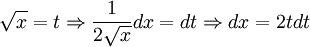 $\sqrt{x}=t \Rightarrow \frac1{2\sqrt x} dx = dt \Rightarrow dx=2tdt$

קיבלנו 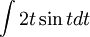$\int 2t\sin t dt$ . ניתן לראות ע"י אינטגרציה בחלקים ( 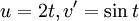$u=2t, v'=\sin t$ ) כי האינטגרל הוא 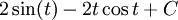$2\sin(t)- 2t\cos t + C$ ולכן מתקיים:

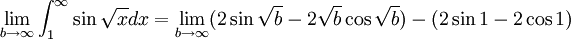$\lim_{b\to\infty} \int_1^\infty \sin\sqrt x dx = \lim_{b\to\infty} (2\sin\sqrt b - 2\sqrt{b}\cos\sqrt{b})-(2\sin1-2\cos1)$ וזה כמובן לא מתכנס ולכן האינטגרל מתבדר

שאלה 4

הפרכה: ניקח את 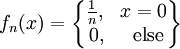$f_n(x)=\begin{Bmatrix} \frac 1n ,\ \ x=0\\ 0,\ \ \ \ \mathrm{else} \end{Bmatrix}$ . נראה כי 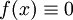$f(x)\equiv 0$ וההתכנסות היא במ"ש (קל להוכיח).

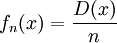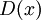עוד פונקציה שמפריכה היא $f_n(x)=\frac{D(x)}{n}$ כאשר $D(x)$ היא פונקציית דיריכלה. זאת אומרת,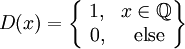 $D(x)=\begin{Bmatrix}\ 1 ,\ \ x \in \mathbb{Q}\\ 0,\ \ \ \ \mathrm{else} \end{Bmatrix}$

שאלה 6

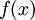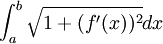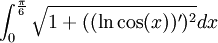נזכור כי הנוסחה לחישוב אורך עקומה של $f(x)$ בקטע $[a,b]$ היא $\int_a^b \sqrt{1+(f'(x))^2} dx$ ולכן אנחנו מחפשים את $\int_0^{\frac{\pi}6}\sqrt{1+((\ln\cos(x))')^2}dx$ .

מתקיים: 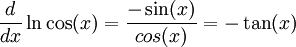$\frac{d}{dx}\ln\cos(x) = \frac{-\sin(x)}{cos(x)}=-\tan(x)$ .

כמו כן, 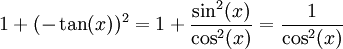$1+(-\tan(x))^2=1+\frac{\sin^2(x)}{\cos^2(x)}=\frac1{\cos^2(x)}$ .

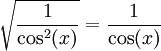נראה כי $\forall x \in [0,\frac{\pi}6] :\cos(x)>0$ ולכן $\sqrt{\frac{1}{\cos^2(x)}}=\frac1{\cos(x)}$ ולא צריך לדאוג לגבי הסימן המכנה.

נרצה לחשב כעת את $\int_0^{\frac{\pi}6} \frac{1}{\cos(x)} dx$

@@ שורה 69: / שורה 69: @@
 <math>x+\frac{2}{3}\ln|x-1|-\frac{1}{3}\ln|x^2+x+1|-\frac{2}{\sqrt{3}}\arctan\frac{2x+1}{\sqrt{3}}+c</math>
+=שאלה 3=
+==סעיף א==
+צריך לבדוק אם <math>\int_1^\infty \sin\sqrt{x}dx</math> מתכנס או מתבדר.
+הצעה לפתרון: ננסה לחשב את <math>\lim_{b\to\infty} \int_1^b \sin \sqrt{x} dx</math>. נסתכל על <math>\int \sin\sqrt x dx</math>. ע"י החלפת משתנים נקבל <math>\sqrt{x}=t \Rightarrow \frac1{2\sqrt x} dx = dt \Rightarrow dx=2tdt</math>
+קיבלנו <math>\int 2t\sin t dt</math>. ניתן לראות ע"י אינטגרציה בחלקים (<math>u=2t, v'=\sin t</math>) כי האינטגרל הוא <math>2\sin(t)- 2t\cos t + C</math> ולכן מתקיים:
+<math>\lim_{b\to\infty} \int_1^\infty \sin\sqrt x dx = \lim_{b\to\infty} (2\sin\sqrt b - 2\sqrt{b}\cos\sqrt{b})-(2\sin1-2\cos1)</math> וזה כמובן לא מתכנס ולכן האינטגרל מתבדר
 =שאלה 4=

הבדלים בין גרסאות בדף "חשבון אינפיניטיסימלי 2 - פתרון מועד א תשע"ג"

גרסה מ־18:31, 9 ביולי 2013

תוכן עניינים

שאלה 2

סעיף א

סעיף ב

שאלה 3

סעיף א

שאלה 4

שאלה 6

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים