מבחן השורש של קושי
מתוך Math-Wiki
מבחן השורש של קושי לטורים חיוביים
יהי 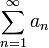 טור חיובי. אזי:
טור חיובי. אזי:
- אם
![\limsup\limits_{n\to\infty}\sqrt[n]{a_n}>1](/images/math/8/1/8/8187311a342331109b5648d549afca00.png) הטור מתבדר
הטור מתבדר
- אם
![\limsup\limits_{n\to\infty}\sqrt[n]{a_n}<1](/images/math/a/3/0/a309ceaf76090d7acd59cea36ccadab4.png) הטור מתכנס
הטור מתכנס
- אם
![\limsup\limits_{n\to\infty}\sqrt[n]{a_n}=1](/images/math/2/3/a/23a1e4f7c0e6f296ce49702a948f1a3b.png) לא ניתן לקבוע על פי מבחן זה.
לא ניתן לקבוע על פי מבחן זה.
הוכחה
נניח כי ![\limsup\limits_{n\to\infty}\sqrt[n]{a_n}=d>1](/images/math/2/e/f/2efcd01e4edba940f5d55cef49320778.png) . נבחר את תת הסדרה המתכנסת לגבול העליון:
. נבחר את תת הסדרה המתכנסת לגבול העליון:
לכן החל ממקום מסוים בסדרה, ![\sqrt[n_k]{a_{n_k}}>\dfrac{d+1}{2}>1](/images/math/b/b/b/bbb54d345813729f07273f442841920d.png) .
.
לכן 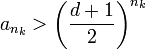
לכן 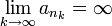
לכן בפרט 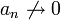
ולכן הטור מתבדר.
כעת, נניח כי ![\limsup\limits_{n\to\infty}\sqrt[n]{a_n}=d<1](/images/math/4/7/2/47237aa3e1c61d5867950c395e9133cb.png) .
.
לכן החל ממקום מסוים בסדרה, ![\sqrt[n]{a_n}<\dfrac{1+d}{2}<1](/images/math/0/a/7/0a7de53091740ba4bbc5218e7d6a9cd6.png)
לכן 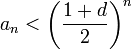
אבל 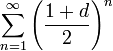 הוא טור הנדסי מתכנס
הוא טור הנדסי מתכנס
לכן לפי מבחן ההשוואה הראשון לטורים חיוביים, הטור שלנו מתכנס.
הטורים 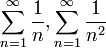 הם דוגמאות להתכנסות והתבדרות כאשר הגבול שווה ממש ל-1.
הם דוגמאות להתכנסות והתבדרות כאשר הגבול שווה ממש ל-1.
![\lim\limits_{k\to\infty}\sqrt[n_k]{a_{n_k}}=d](/images/math/2/8/a/28aad26c7ff9adac37e60af78056f0d1.png)