הבדלים בין גרסאות בדף "מבחני התכנסות לאינטגרלים לא אמיתיים"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
שורה 5: שורה 5:
 
אזי מתקיים:
 
אזי מתקיים:
  
−
<math> \int_a^{\infty} g(x)dx </math> מתכנס <math> \int_a^{\infty} f(x)dx \Leftarrow</math> מתכנס
+
<math> \int_a^{\infty} g(x)\mathrm{d}x </math> מתכנס <math> \int_a^{\infty} f(x)\mathrm{d}x \Leftarrow</math> מתכנס
  
−
<math> \int_a^{\infty} f(x)dx </math> מתבדר <math> \int_a^{\infty} g(x)dx \Leftarrow</math> מתבדר
+
<math> \int_a^{\infty} f(x)\mathrm{d}x </math> מתבדר <math> \int_a^{\infty} g(x)\mathrm{d}x \Leftarrow</math> מתבדר
  
 
<font size=4 color=#a7adcd>
 
<font size=4 color=#a7adcd>
שורה 13: שורה 13:
 
</font>
 
</font>
  
−
קבע האם <math> \int_1^\infty \frac{\arctan(x)}{x} dx </math> מתכנס או מתבדר
+
קבע האם <math> \int_1^\infty \frac{\arctan(x)}{x} \mathrm{d}x </math> מתכנס או מתבדר
  
 
'''פתרון.'''
 
'''פתרון.'''
שורה 20: שורה 20:
 
<math> \forall_{x>1}: \arctan(x)>\arctan(1)=\frac{\pi}{4}>0 </math> ולכן <math> \forall_{x>1}: \frac{\arctan(x)}{x}>\frac{\pi}{4x}>0 </math>
 
<math> \forall_{x>1}: \arctan(x)>\arctan(1)=\frac{\pi}{4}>0 </math> ולכן <math> \forall_{x>1}: \frac{\arctan(x)}{x}>\frac{\pi}{4x}>0 </math>
  
−
<math> \int_1^\infty \frac{\pi}{4x}dx= \frac{\pi}{4} \int_1^\infty \frac1x dx </math> מתבדר, ולכן, עפ"י מבחן ההשוואה הראשון, האינטגרל שלנו גם כן מתבדר.
+
<math> \int_1^\infty \frac{\pi}{4x}\mathrm{d}x= \frac{\pi}{4} \int_1^\infty \frac1x \mathrm{d}x </math> מתבדר, ולכן, עפ"י מבחן ההשוואה הראשון, האינטגרל שלנו גם כן מתבדר.
  
 
===מבחן ההשוואה הגבולי===
 
===מבחן ההשוואה הגבולי===
שורה 32: שורה 32:
 
'''אזי:'''
 
'''אזי:'''
  
−
אם <math>L>0 , L\in\mathbb{R}</math> אז <math>\int_a^\infty f(x)dx</math> ו- <math>\int_a^\infty g(x)dx</math> מתכנסים או מתבדרים יחדיו ("חברים").
+
אם <math>L>0 , L\in\mathbb{R}</math> אז <math>\int_a^\infty f(x)\mathrm{d}x</math> ו- <math>\int_a^\infty g(x)\mathrm{d}x</math> מתכנסים או מתבדרים יחדיו ("חברים").
  
−
אם <math>L=0</math> אז <math>\int_a^\infty g(x)dx</math> מתכנס <math>\int_a^\infty f(x)dx \Leftarrow</math> מתכנס.
+
אם <math>L=0</math> אז <math>\int_a^\infty g(x)\mathrm{d}x</math> מתכנס <math>\int_a^\infty f(x)\mathrm{d}x \Leftarrow</math> מתכנס.
  
−
אם <math>L=\infty</math> אז <math>\int_a^\infty f(x)dx</math> מתכנס <math>\int_a^\infty g(x)dx \Leftarrow</math> מתכנס.
+
אם <math>L=\infty</math> אז <math>\int_a^\infty f(x)\mathrm{d}x</math> מתכנס <math>\int_a^\infty g(x)\mathrm{d}x \Leftarrow</math> מתכנס.

גרסה מ־12:00, 11 במאי 2013

אינטגרלים לא אמיתיים מסוג ראשון

מבחן ההשוואה הראשון

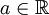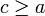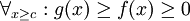יהי a \in \mathbb{R} , ותהי נק' c\geq a כך שמתקיים \forall_{x\geq c} : g(x)\geq f(x)\geq 0 .

אזי מתקיים:

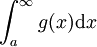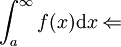\int_a^{\infty} g(x)\mathrm{d}x מתכנס \int_a^{\infty} f(x)\mathrm{d}x \Leftarrow מתכנס

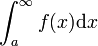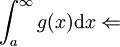\int_a^{\infty} f(x)\mathrm{d}x מתבדר \int_a^{\infty} g(x)\mathrm{d}x \Leftarrow מתבדר

דוגמא.

קבע האם 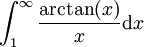\int_1^\infty \frac{\arctan(x)}{x} \mathrm{d}x מתכנס או מתבדר

פתרון. נשים לב כי 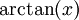\arctan(x) היא פונקציה מונוטונית עולה ולכן בתחום האינטגרציה:

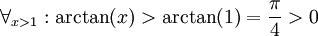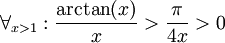
\forall_{x>1}: \arctan(x)>\arctan(1)=\frac{\pi}{4}>0 ולכן \forall_{x>1}: \frac{\arctan(x)}{x}>\frac{\pi}{4x}>0

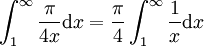\int_1^\infty \frac{\pi}{4x}\mathrm{d}x= \frac{\pi}{4} \int_1^\infty \frac1x \mathrm{d}x מתבדר, ולכן, עפ"י מבחן ההשוואה הראשון, האינטגרל שלנו גם כן מתבדר.

מבחן ההשוואה הגבולי

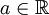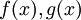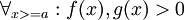
יהי a \in \mathbb{R} , ותהיינה שתי פונקציות f(x), g(x) כך ש: \forall_{x>=a}:f(x),g(x)>0

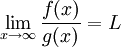
יהי הגבול: \lim_{x\to\infty}\frac{f(x)}{g(x)}=L

אזי:

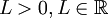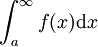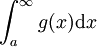אם L>0 , L\in\mathbb{R} אז \int_a^\infty f(x)\mathrm{d}x ו- \int_a^\infty g(x)\mathrm{d}x מתכנסים או מתבדרים יחדיו ("חברים").

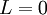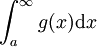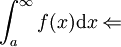אם L=0 אז \int_a^\infty g(x)\mathrm{d}x מתכנס \int_a^\infty f(x)\mathrm{d}x \Leftarrow מתכנס.

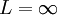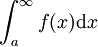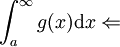אם L=\infty אז \int_a^\infty f(x)\mathrm{d}x מתכנס \int_a^\infty g(x)\mathrm{d}x \Leftarrow מתכנס.

מקור: https://math-wiki.com/index.php?title=מבחני_התכנסות_לאינטגרלים_לא_אמיתיים&oldid=34037