הבדלים בין גרסאות בדף "מד"ר - משוואות דיפרנציאליות רגילות - ארז שיינר"
מתוך Math-Wiki
(←הרצאה 1 הקדמה) |
(←המשוואה y'=r\cdot y) |
||
| שורה 42: | שורה 42: | ||
===המשוואה <math>y'=r\cdot y</math>=== | ===המשוואה <math>y'=r\cdot y</math>=== | ||
| − | |||
*בהמשך הקורס נעסוק בשאלה האם למשוואה דיפרנציאלית יש פתרון, וכמה פתרונות יש למשוואה. | *בהמשך הקורס נעסוק בשאלה האם למשוואה דיפרנציאלית יש פתרון, וכמה פתרונות יש למשוואה. | ||
*מידי פעם נחזור ונפתור את המשוואה הזו בכלים שונים. | *מידי פעם נחזור ונפתור את המשוואה הזו בכלים שונים. | ||
| שורה 54: | שורה 53: | ||
*על מנת לחשב את הקבוע C עבור המקרה של ריבית דריבית, עלינו לדעת כמה כסף היה בחשבון בזמן t=0. | *על מנת לחשב את הקבוע C עבור המקרה של ריבית דריבית, עלינו לדעת כמה כסף היה בחשבון בזמן t=0. | ||
| + | *שימו לב שלכל תנאי התחלה קיבלנו פתרון '''יחיד'''. | ||
גרסה מ־11:46, 4 במרץ 2018
תוכן עניינים
הרצאה 1 הקדמה
- משוואה דיפרנציאלית מכילה את המשתנה, הפונקציה ונגזרותיה.
- בחקירת פונקציות, במציאת תחומי עלייה וירידה, אנו פותרים את המשוואה
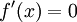 . האם זו משוואה דיפרנציאלית?
. האם זו משוואה דיפרנציאלית? - לא, כיוון שבמשוואות דיפרנציאלית אנו מחפשים פונקציה שמקיימת את המשוואה לכל ערך של המשתנה.
- כאן הפונקציה נתונה, ואנו מחפשים ערך של המשתנה שמקיים את המשוואה.
נפילה חופשית
- גוף הנופל חופשית נופל בתאוצה שבקירוב היא קבועה
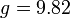 .
. - נסמן ב
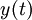 את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ)
את הגובה של הגוף (כאשר הכיוון החיובי הוא לכיוון כדור הארץ) 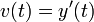 היא המהירות
היא המהירות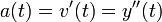 היא התאוצה.
היא התאוצה.- לכן על מנת לדעת את מיקומו של הגוף בכל נקודה בזמן, עלינו לפתור את המשוואה
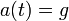 , הרי התאוצה קבועה.
, הרי התאוצה קבועה.
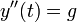
- לכן
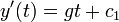
- לכן
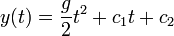
- כיצד נחשב את הקבועים? לפי תנאי ההתחלה.
- נסמן את הגובה ההתחלתי בתור 0 (נזכור כי הכיוון החיובי הוא לכיוון כדור הארץ). ולכן
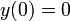 ולכן
ולכן 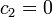
- נניח כי המהירות ההתחלתית גם היא הייתה 0 ולכן
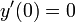 ולכן גם
ולכן גם 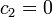 .
.
ריבית דריבית
- נניח שסכום הכסף בבנק לאורך זמן מתואר על ידי הפונקציה
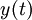 .
. - נניח שאנו מרוויחים תשואה של 2 אחוז בשנה, לכן לאחר שנה יתקיים כי
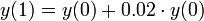 .
. - אבל מה היה קורה אילו הבנק היה משלם את הריבית פעם בחצי שנה?
- בחצי השנה הראשונה נקבל מחצית מהריבית
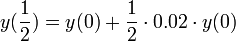
- ובחצי השנה השנייה נקבל מחצית מהריבית, אך סכום הקרן שלנו כבר גדל
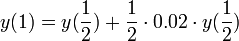
- סה"כ
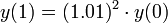
- בחצי השנה הראשונה נקבל מחצית מהריבית
- זה גדול יותר מהריבית השנתית, כיוון שצברנו ריבית על הקרן וגם על הריבית החצי שנתית.
- האם יש דרך להפוך את התהליך לרציף?
- כלומר, בהנתן שתי נקודות זמן קרובות אנו מעוניינים לקבל את הריבית היחסית על הזמן שעבר:
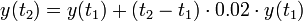
- נעביר אגף ונחלק
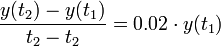
- אם נשאיף
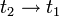 נקבל כי
נקבל כי 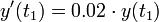
- כלומר אנו מעוניינים בפונקציה שמקיימת את המשוואה הדיפרנציאלית
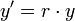 כאשר
כאשר 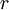 היא הריבית השנתית.
היא הריבית השנתית.
המשוואה 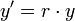
- בהמשך הקורס נעסוק בשאלה האם למשוואה דיפרנציאלית יש פתרון, וכמה פתרונות יש למשוואה.
- מידי פעם נחזור ונפתור את המשוואה הזו בכלים שונים.
- כעת נשים לב כי:
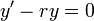
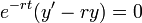
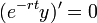
- כיוון שהנגזרת שווה אפס הפונקציה קבועה
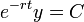
- סה"כ
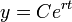
- על מנת לחשב את הקבוע C עבור המקרה של ריבית דריבית, עלינו לדעת כמה כסף היה בחשבון בזמן t=0.
- שימו לב שלכל תנאי התחלה קיבלנו פתרון יחיד.