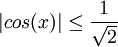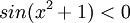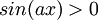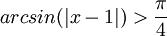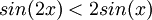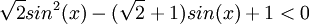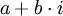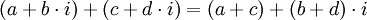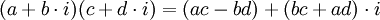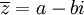הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/4"
מתוך Math-Wiki
(←מספרים מרוכבים) |
(←מספרים מרוכבים) |
||
| שורה 80: | שורה 80: | ||
| − | '''תרגיל''' הוכח שלכל מספר מרוכב <math>z</math> קיים מספר מרוכב <math> | + | '''תרגיל''' הוכח שלכל מספר מרוכב <math>z</math> קיים מספר מרוכב <math>z^{-1}</math> כך ש <math>z\cdot z^{-1} = 1</math>. |
| − | '''פתרון''': <math> | + | '''פתרון''': <math>z^{-1}=\frac{\overline{z}}{|z|^2}</math> |
::הערה: באופן כללי נסמן <math>z^{-1}=\frac{1}{z}</math> | ::הערה: באופן כללי נסמן <math>z^{-1}=\frac{1}{z}</math> | ||
| − | |||
| שורה 92: | שורה 91: | ||
'''תרגיל''' חשב את הביטוי <math>\frac{5+2i}{2-3i}</math> | '''תרגיל''' חשב את הביטוי <math>\frac{5+2i}{2-3i}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''הגדרה''': עבור מספר מרוכב <math>z=a+bi</math> | ||
| + | |||
| + | ::החלק הממשי <math>Re(z)=a</math> | ||
| + | |||
| + | ::החלק המדומה <math>Im(z)=b</math> | ||
| + | |||
| + | |||
| + | לדוגמא: | ||
| + | |||
| + | |||
| + | <math>Im(a-bi) = -b</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''תרגיל''': הוכח כי <math>|z|\geq |Re(z)|</math> | ||
| + | |||
| + | |||
| + | '''תרגיל''': הוכח את '''אי-שיוויון המשולש''' <math>|z_1+z_2|\leq |z_1|+|z_2|</math> | ||
גרסה מ־07:20, 8 באוגוסט 2012
פונקציות טריגונומטריות הופכיות
ניתן להגדיר פונקציה הופכית רק כאשר לכל איבר בתמונה קיים מקור יחיד. לכל פונקציה טריגונומטרית נבחר את התחום המתאים.
תרגיל: הוכח כי 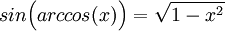
תרגילים
מצא לאילו ערכי x מתקיימים אי השיוויונים הבאים:
מספרים מרוכבים
נביט באוסף האיברים מהצורה
כאשר 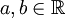 והאות i הינה לצורך סימון בלבד. נקרא לאוסף זה מספרים מרוכבים.
והאות i הינה לצורך סימון בלבד. נקרא לאוסף זה מספרים מרוכבים.
נגדיר פעולות חיבור וכפל בין מספרים מרוכבים:
שימו לב כי 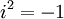
בנוסף לכל מספר מרוכב 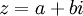 נגדיר את הצמוד המרוכב:
נגדיר את הצמוד המרוכב:
תרגיל חשב את 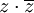
פתרון 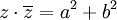
- הערה: נסמן
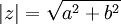
- הערה: נסמן
תרגיל הוכח שלכל מספר מרוכב 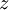 קיים מספר מרוכב
קיים מספר מרוכב 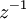 כך ש
כך ש 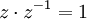 .
.
פתרון: 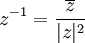
- הערה: באופן כללי נסמן
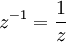
- הערה: באופן כללי נסמן
תרגיל חשב את הביטוי 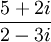
הגדרה: עבור מספר מרוכב 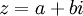
- החלק הממשי
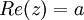
- החלק הממשי
- החלק המדומה
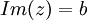
- החלק המדומה
לדוגמא:
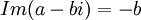
תרגיל: הוכח כי 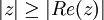
תרגיל: הוכח את אי-שיוויון המשולש 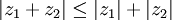
![arcsin(x):[-1,1]\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]](/images/math/a/d/8/ad87e9d8d48f94ca443b202a6ac1c6d9.png)
![arccos(x):[-1,1]\rightarrow [0,\pi]](/images/math/4/4/5/445e4a4ac23bf5bc584557717c908d37.png)
![arctan(x):[-\infty,\infty]\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]](/images/math/4/9/7/497e8e90b0de743a2bbaf31105b5923c.png)