משתמש:אור שחף/133 - הרצאה/22.3.11
תוכן עניינים
האינטגרל המסויים (המשך)
דוגמאות
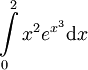 .
.
- שיטה א - נתעלם מהגבולות עד למציאת הפונקציה הקדומה: נציב
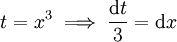 . לכן
. לכן ![\int=\int\frac{e^t}3\mathrm dt=\left[\frac{e^t}3\right]_{x=0}^2=\left[\frac{e^{x^3}}3\right]_{x=0}^2=\frac{e^8-1}3](/images/math/2/f/7/2f70b43f67da9093041bd4de8dcda478.png) .
. 
- דרך ב - נחליף את הגבולות במהלך החישוב:
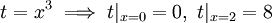 ולכן
ולכן ![\int=\int\limits_0^8\frac{e^t}3\mathrm dt=\left[\frac{e^t}3\right]_{t=0}^8=\frac{e^8-1}3](/images/math/5/a/5/5a54d171dc3b2e66c12c66e3be268fb0.png) .
. 
- שיטה א - נתעלם מהגבולות עד למציאת הפונקציה הקדומה: נציב
- נחשב שטח עיגול בעל רדיוס r.
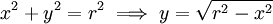 . לכן השטח הוא
. לכן השטח הוא 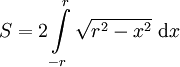 . נציב
. נציב 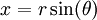 ואז
ואז ![\begin{align}S&=2\int\limits_{-\frac\pi2}^{\frac\pi2}\sqrt{r^2-r^2\sin^2(\theta)}\ r\cos(\theta)\mathrm d\theta\\&=2\int\limits_{-\frac\pi2}^{\frac\pi2}r^2\cos^2(\theta)\mathrm d\theta\\&=2r^2\int\limits_{-\frac\pi2}^{\frac\pi2}\frac{\cos(2\theta)+1}2\mathrm d\theta\\&=2r^2\left[\frac{\frac12\sin(2\theta)+\theta}2\right]_{\theta=-\frac\pi2}^{\frac\pi2}\\&=2r^2\left(\frac14\cdot0+\frac\pi4-\frac14\cdot0+\frac\pi4\right)\\&=\pi r^2\end{align}](/images/math/4/3/6/4366dfcd64be516dd528228bb8bd57a0.png)
 הערה: כאשר החלפנו את גבולות האינטגרציה בהצגה
הערה: כאשר החלפנו את גבולות האינטגרציה בהצגה 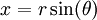 היינו צריכים לבחור
היינו צריכים לבחור 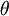 כך ש-
כך ש-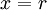 , אבל עבור מעגל שרדיוסו r מתחלק ב-4 עם שארית 1 היינו יכולים לבחור גם
, אבל עבור מעגל שרדיוסו r מתחלק ב-4 עם שארית 1 היינו יכולים לבחור גם 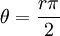 כי אז
כי אז 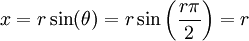 , ועבור
, ועבור 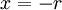 יכולנו לבחור
יכולנו לבחור 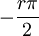 . אם כן היינו מוצאים הטעות נובעת מכך שקבענו ש-
. אם כן היינו מוצאים הטעות נובעת מכך שקבענו ש-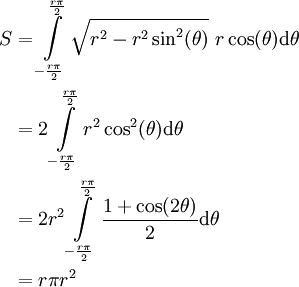
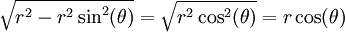 , מה שנכון רק כאשר
, מה שנכון רק כאשר 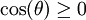 . הטווח של האינטגרציה היה
. הטווח של האינטגרציה היה ![\left[-\frac{r\pi}2,\frac{r\pi}2\right]](/images/math/9/c/e/9ce51cd7682cb87fd3c5249ea9da5741.png) , שכולל תחומים בהם
, שכולל תחומים בהם 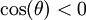 . בתחומים אלה צריך לבחור
. בתחומים אלה צריך לבחור 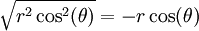 ולחלק את הקטע
ולחלק את הקטע ![\left[-\frac{r\pi}2,\frac{r\pi}2\right]](/images/math/9/c/e/9ce51cd7682cb87fd3c5249ea9da5741.png) לתחומים שונים לפי הסימן של
לתחומים שונים לפי הסימן של 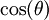 .
.
יישומים של אינטגרציה
-
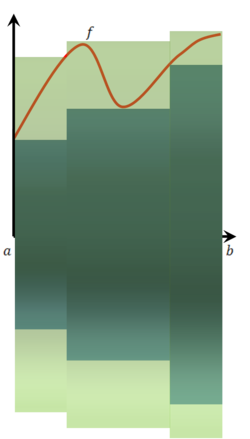
שטח
אם בקטע![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתקיים
מתקיים 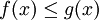 כבר ראינו שהשטח בין הגרפים הוא
כבר ראינו שהשטח בין הגרפים הוא 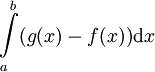 .
. -
נפח של גוף סיבוב
נסובב את השטח מתחת לגרף
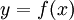 בין a ל-b סביב ציר ה-x ונחשב את הנפח הנוצר. עבור
בין a ל-b סביב ציר ה-x ונחשב את הנפח הנוצר. עבור 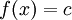 קבוע הסיבוב יוצר גליל שנפחו ידוע לנו:
קבוע הסיבוב יוצר גליל שנפחו ידוע לנו: 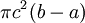 . כעת נניח ש-
. כעת נניח ש-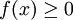 רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונחשב את הנפח הנוצר ע"י סיבוב הגרף. נקח חלוקה כלשהי P של
ונחשב את הנפח הנוצר ע"י סיבוב הגרף. נקח חלוקה כלשהי P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ,
, 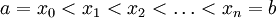 . תחילה נעיין בנפח הנוצר כאשר אותו חלק מהגרף שמעל
. תחילה נעיין בנפח הנוצר כאשר אותו חלק מהגרף שמעל ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) מסתובב סביב ציר ה-x. עפ"י המשפט השני של וירשטרס יש ל-f מקסימום
מסתובב סביב ציר ה-x. עפ"י המשפט השני של וירשטרס יש ל-f מקסימום 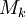 ומינימום
ומינימום 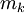 בקטע זה. נסמן ב-
בקטע זה. נסמן ב-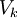 הנפח שנוצר ע"י חלק זה של הגרף של f. אז מתקיים
הנפח שנוצר ע"י חלק זה של הגרף של f. אז מתקיים 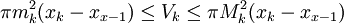 . יוצא שהנפח בסה"כ הוא
. יוצא שהנפח בסה"כ הוא 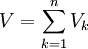 ומתקיים
ומתקיים 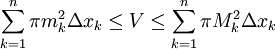 . נשים לב שהסכום בצד ימין הוא בדיוק
. נשים לב שהסכום בצד ימין הוא בדיוק 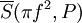 ובצד שמאל
ובצד שמאל 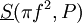 עבור החלוקה P. נשאיף
עבור החלוקה P. נשאיף 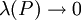 וכיוון ש-f רציפה גם
וכיוון ש-f רציפה גם 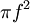 רציפה ולכן שני הסכומים הנ"ל שואפים לאותו הגבול:
רציפה ולכן שני הסכומים הנ"ל שואפים לאותו הגבול: 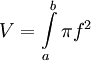 .
.
דוגמאות
- נחשב נפח של כדור בעל רדיוס r:
![\begin{align}V&=\pi\int\limits_{-r}^r f^2\\&=\pi\int\limits_{-r}^r \left(r^2-x^2\right)\mathrm dx\\&=\pi\left[r^2x-\frac{x^3}3\right]_{x=-r}^r\\&=2\pi\left(r^3-\frac{r^3}3\right)\\&=\frac43\pi r^3\end{align}](/images/math/4/7/6/476aa511df8ebbe90ef5eb9a37e6e999.png)

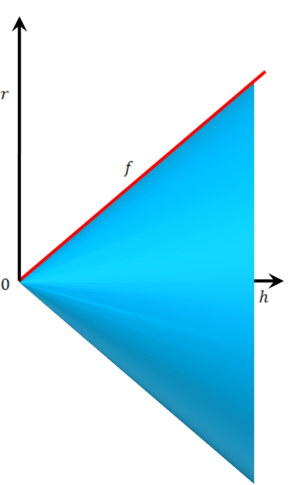
- נחשב נפח של חרוט בעל גובה h ורדיוס בסיס r. בסרטוט משמאל יש גרף סיבוב המתקבל מסיבוב משולש סביב ציר ה-x. הפונקציה היא
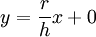 ולפיכך הנפח הוא כלומר נפח החרוט הוא שליש מנפח הגליל בעל אותו גובה ורדיוס בסיסים.
ולפיכך הנפח הוא כלומר נפח החרוט הוא שליש מנפח הגליל בעל אותו גובה ורדיוס בסיסים.![\begin{align}V&=\pi\int\limits_0^h\left(\frac rhx\right)^2\mathrm dx\\&=\pi\left(\frac rh\right)^2\int\limits_0^h x^2\mathrm dx\\&=\pi\left(\frac rh\right)^2\left[\frac{x^3}3\right]_{x=0}^h\\&=\frac{\pi r^2h}3\end{align}](/images/math/f/d/1/fd1c36855722c88a98037c7b118721e8.png)

- נחשב נפח של כדור בעל רדיוס r:
-
ממוצע
תהא f מוגדרת ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונחשב את הממוצע של f בקטע זה באופן הבא: לכל
ונחשב את הממוצע של f בקטע זה באופן הבא: לכל 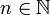 נגדיר חלוקה
נגדיר חלוקה 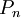 של הקטע לקטעים שווים
של הקטע לקטעים שווים 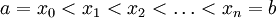 . כאשר
. כאשר 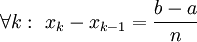 . הממוצע של f בנקודות החלוקה הוא
. הממוצע של f בנקודות החלוקה הוא 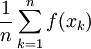 . לפי בחירת
. לפי בחירת  , לכל k מתקיים
, לכל k מתקיים 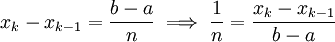 ונובע:
ונובע: 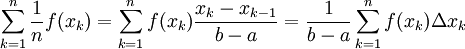 (כאשר
(כאשר 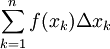 הוא סכום רימן). נשאיף
הוא סכום רימן). נשאיף 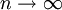 ומכיוון שבמקרה כזה
ומכיוון שבמקרה כזה 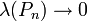 מצאנו שהממוצע של f שואף ל-
מצאנו שהממוצע של f שואף ל-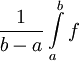 . באותה דרך ניתן לחשב ממוצע של כל פונקציה אינטגרבילית, גם אם היא לא רציפה. גישה אחרת (אינטואיטיבית): אם
. באותה דרך ניתן לחשב ממוצע של כל פונקציה אינטגרבילית, גם אם היא לא רציפה. גישה אחרת (אינטואיטיבית): אם  רציפה אז
רציפה אז 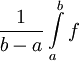 הוא השטח שמתחת לגרף חלקי אורך בסיס השטח, שזה הממוצע.
הוא השטח שמתחת לגרף חלקי אורך בסיס השטח, שזה הממוצע. -
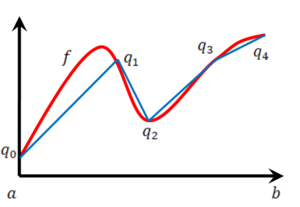
אורך הגרף
עבור פונקציה f רציפה ב-
נניח ש-f' קיימת ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נעשה חלוקה
נעשה חלוקה  של הקטע. החלוקה גורמת לחלוקת הגרף ע"י נקודות
של הקטע. החלוקה גורמת לחלוקת הגרף ע"י נקודות 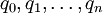 , כאשר לכל k
, כאשר לכל k 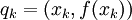 . קירוב סביר לאורך הגרף נתון ע"י
. קירוב סביר לאורך הגרף נתון ע"י 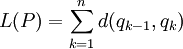 , כאשר
, כאשר 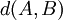 הוא המרחק בין הנקודות A ו-B. מרחק זה שווה ל-
הוא המרחק בין הנקודות A ו-B. מרחק זה שווה ל-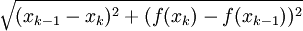 . לכן אורך הגרף L מקיים
. לכן אורך הגרף L מקיים 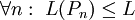 ואפשר להגדיר את L ע"י
ואפשר להגדיר את L ע"י 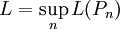 . לפי זה L תמיד מוגדר
. לפי זה L תמיד מוגדר 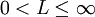 .
.
דוגמה: נגדיר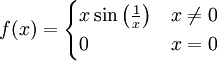 . היא רציפה בקטע הסגור
. היא רציפה בקטע הסגור ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) אבל אורך הגרף הוא
אבל אורך הגרף הוא 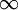 .
.
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונקח חלוקה P כלשהי. כבר ראינו ש-(ע"פ משפט לגראנז' יש
ונקח חלוקה P כלשהי. כבר ראינו ש-(ע"פ משפט לגראנז' יש
 כאלה כך ש-
כאלה כך ש-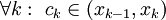 ) והגענו לסכום רימן עבור הפונקציה
) והגענו לסכום רימן עבור הפונקציה 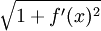 . היה נתון ש-
. היה נתון ש-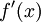 רציפה ולכן גם
רציפה ולכן גם 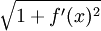 רציפה, וסכומי רימן אלה שואפים לאינטגרל
רציפה, וסכומי רימן אלה שואפים לאינטגרל 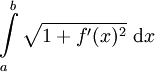 . השערה מאוד סבירה היא שזהו אורך הגרף
. השערה מאוד סבירה היא שזהו אורך הגרף 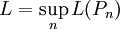 . נוכיח זאת: נגדיר
. נוכיח זאת: נגדיר 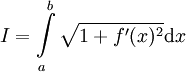 וכן
וכן 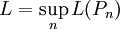 ונניח
ונניח 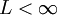 . יהי
. יהי 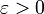 נתון. לפי הגדרת הסופרימום קיימת חלוקה מסויימת Q של
נתון. לפי הגדרת הסופרימום קיימת חלוקה מסויימת Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-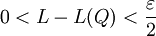 . אם Q' עידון של Q אז
. אם Q' עידון של Q אז 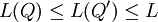 ולכן
ולכן 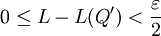 . כעת נתון ש-
. כעת נתון ש-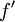 רציפה ולכן
רציפה ולכן 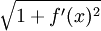 אינטגרבילית ב-
אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . לפיכך קיימת
. לפיכך קיימת 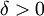 כך שאם P חלוקה כלשהי של
כך שאם P חלוקה כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-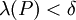 ואם S סכום רימן כלשהו הבנוי על P אז
ואם S סכום רימן כלשהו הבנוי על P אז 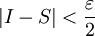 . לבסוף נבחר P להיות עידון כלשהו של Q כך ש-
. לבסוף נבחר P להיות עידון כלשהו של Q כך ש-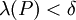 . כבר למדנו ש-
. כבר למדנו ש-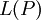 הוא סכום רימן S עבור האינטגרל I שבנוי על P. מכל זה נסיק
הוא סכום רימן S עבור האינטגרל I שבנוי על P. מכל זה נסיק 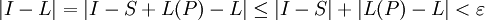 ז"א I ו-L הם שני מספרים קבועים שהפרשם קטן מ-
ז"א I ו-L הם שני מספרים קבועים שהפרשם קטן מ- ומכאן נובע שהם שווים.
ומכאן נובע שהם שווים.