משתמש:אור שחף/133 - הרצאה/29.3.11
תוכן עניינים
מבוא לאינטגרציה נומרית (המשך)
-
שיטת הטרפזים
נעשה חלוקה שווה של![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: 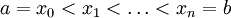 , כאשר
, כאשר 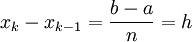 . חלוקת הקטע
. חלוקת הקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) משרה חלוקת הגרף
משרה חלוקת הגרף 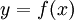 . נחבר את הנקודות האלה בגרף ע"י קווים ישרים, וכך ניצור איחוד של n טרפזים (במקום מלבנים בשיטה של סכומי רימן), והשטח הכולל של הטרפזים הוא קירוב של האינטגרל. לטרפז שמעל
. נחבר את הנקודות האלה בגרף ע"י קווים ישרים, וכך ניצור איחוד של n טרפזים (במקום מלבנים בשיטה של סכומי רימן), והשטח הכולל של הטרפזים הוא קירוב של האינטגרל. לטרפז שמעל ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) יש רוחב h ושני גבהים
יש רוחב h ושני גבהים 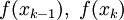 . לכן שטח אותו טרפז הוא
. לכן שטח אותו טרפז הוא 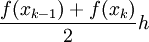 , והקירוב לאינטגרל הוא
, והקירוב לאינטגרל הוא 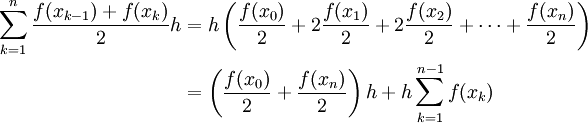
נותר לחשב את סדר הגודל של הטעות. נסמן לכל פונקציה g
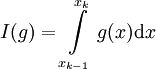 וכן
וכן 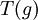 הקירוב של
הקירוב של 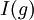 ע"י טרפז. עתה נתמקד באחד הקטעים
ע"י טרפז. עתה נתמקד באחד הקטעים ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) ונעריך את הטעות בו, השווה ל-
ונעריך את הטעות בו, השווה ל-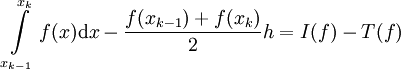 . נשים לב כי אם f לינארית בקטע אז הטעות היא 0.
. נשים לב כי אם f לינארית בקטע אז הטעות היא 0.
כעת נניח ש-f בעלת שתי נגזרות רציפות ב-
לפיכך![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונסמן
ונסמן ![M=\max_{x\in[a,b]} |f''(x)|](/images/math/e/0/6/e06ff2b483398a702e1414d12af29bb6.png) . נפתח את f לפיתוח טיילור סביב הנקודה
. נפתח את f לפיתוח טיילור סביב הנקודה 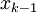 :
: 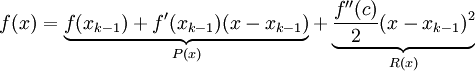 , כאשר P הוא הפיתוח הלינארי של f ו-R השארית ממנו.
, כאשר P הוא הפיתוח הלינארי של f ו-R השארית ממנו.
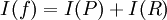 ,
, 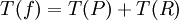 והשארית
והשארית 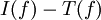 היא
היא 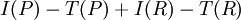 , ומכיוון ש-P לינארית
, ומכיוון ש-P לינארית 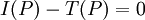 , כלומר השארית היא
, כלומר השארית היא 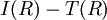 . נחשב: וכן
. נחשב: וכן![\begin{align}|I(R)|&=\left|\int\limits_{x_{k-1}}^{x_k} \frac{f''(c)}2 (x-x_k)^2\mathrm dx\right|\\&=\int\limits_{x_{k-1}}^{x_k} \frac{|f''(c)|}2 (x-x_k)^2\mathrm dx\\&\le\frac M2\left[\frac{(x-x_{k-1})^3}3\right]_{x=x_{x-1}}^{x_k}\\&=\frac M2\frac{(x_k-x_{k-1})^3}3\\&=\frac {Mh^3}6\end{align}](/images/math/6/0/5/6057f385bc6de149ecf937f88e09f2ee.png)
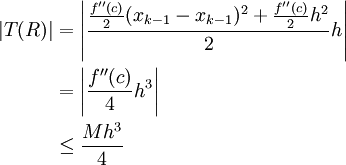
בסה"כ הטעות בקטע
![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) חסומה ע"י
חסומה ע"י 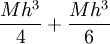 . יש n קטעים כאלה, לכן
. יש n קטעים כאלה, לכן 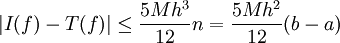 .
.
-
כלל סימפסון (Simpson's Role)
שוב נקרב את
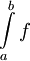 בעזרת חלוקה שווה
בעזרת חלוקה שווה 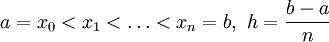 , אלא שהפעם נדרוש ש-n זוגי. הקירוב של סימפסון הוא
, אלא שהפעם נדרוש ש-n זוגי. הקירוב של סימפסון הוא 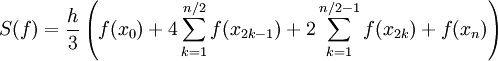 . למעשה, סימפסון מקרב
. למעשה, סימפסון מקרב 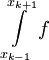 ע"י
ע"י 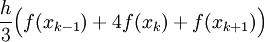
לפני ההוכחה נציג שתי למות להשכלה כללית (באינפי):
- נניח ש-f אינטגרבילית ואי-זוגית בקטע סימטרי
![[-R,R]](/images/math/b/4/b/b4b168e751432fde6a66056effafdfe6.png) אזי
אזי 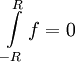 .
הוכחה: נסמן
.
הוכחה: נסמן 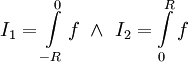 ולכן
ולכן 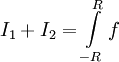 . ב-
. ב-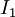 נציב
נציב 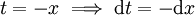 ונקבל
ונקבל 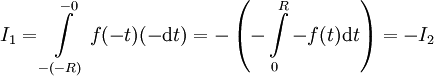 .
. 
- נניח ש-f רציפה בסביבה של
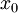 וגזירה בסביבה מנוקבת של
וגזירה בסביבה מנוקבת של 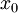 . עוד נניח שקיים
. עוד נניח שקיים 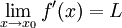 . אזי
. אזי 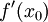 קיים ושווה ל-L.
הוכחה: לפי ההגדרה, אם f גזירה ב-
קיים ושווה ל-L.
הוכחה: לפי ההגדרה, אם f גזירה ב-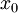 אזי
אזי 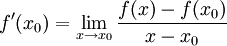 , ולפי משפט לגראנז' זה שווה ל-
, ולפי משפט לגראנז' זה שווה ל-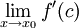 עבור
עבור 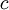 כלשהו בין
כלשהו בין  ל-
ל-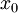 . לכן, כאשר
. לכן, כאשר 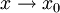 גם
גם 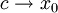 ונקבל
ונקבל 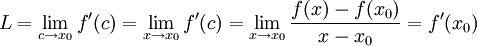 .
. 
נחזור לכלל סימפסון.
שלב א
נניח ש-
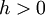 ו-
ו-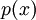 פולינום ממעלה 3 או פחות. נוכיח ש-
פולינום ממעלה 3 או פחות. נוכיח ש-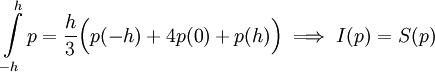 (כאשר לכל f אינטגרבילית ב-
(כאשר לכל f אינטגרבילית ב-![[-h,h]](/images/math/0/c/0/0c0f92ce8a45fddea3c69b9d5071ec3d.png) הגדרנו
הגדרנו 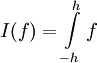 ).
).
הוכחה
לכל פולינום ממעלה 3 (או פחות)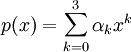 מתקיים
מתקיים ![\begin{align}I(p)&=\sum_{k=0}^3 \int\limits_{-h}^h \alpha_kx^k\mathrm dx\\&=\sum_{k=0}^3 \left[\alpha_k\frac{x^{k+1}}{k+1}\right]_{x=-h}^h\\&=2h\alpha_0+0+\frac23h^3\alpha_2+0\\&=\frac h3\left(6\alpha_0+2h^2\alpha_2\right)\\&=\frac h3\Big(\left(\alpha_0-h\alpha_1+h^2\alpha_2-h^3\alpha_3\right)+4\alpha_0+\left(\alpha_0+h\alpha_1+h^2\alpha_2+h^3\alpha_3\right)\Big)\\&=S(p)\end{align}](/images/math/7/2/4/724577206d17e0446cf56e7ad4ac845a.png)
שלב ב
נניח ש-f בעלת 4 נגזרות רציפות בקטע![[-h,h]](/images/math/0/c/0/0c0f92ce8a45fddea3c69b9d5071ec3d.png) ונסמן
ונסמן ![M=\max_{x\in[-h,h]}\left|f^{(4)}(x)\right|](/images/math/c/3/5/c35b92adb3003ab4e5d2171a05d30527.png) . נעריך את הטעות:
. נעריך את הטעות: 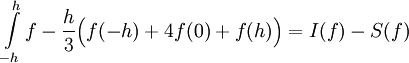 . לצורך זה נשתמש בפיתוח טיילור של f סביב 0 מסדר 3,
. לצורך זה נשתמש בפיתוח טיילור של f סביב 0 מסדר 3, 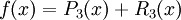 . לכן
. לכן 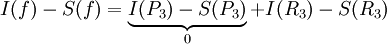 . כזכור
. כזכור 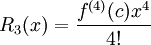 . נעריך:
. נעריך: ![\begin{align}|I(R_3)|&=\left|\int\limits_{-h}^h\frac{f^{(4)}(c)x^4}{4!}\mathrm dx\right|\\&\le\frac M{4!}\int\limits_{-h}^h\left|x^4\right|\mathrm dx\\&=\frac M{24}\left[\frac{x^5}5\right]_{x=-h}^h\\&=\frac{Mh^5}{60}\end{align}](/images/math/a/2/c/a2c062b9f78b0647d29b9e2e9e2c212d.png)
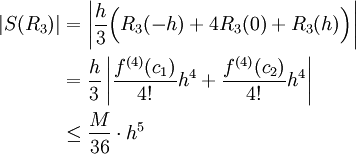
מכל זה, יוצא ש:
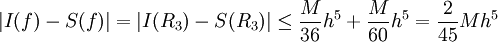 .
.
שלב ג
נוכיח כי לכל k שעבורו
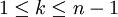 מתקיים
מתקיים 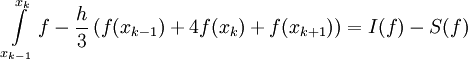
הוכחה
באינטגרל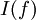 נציב
נציב 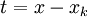 כדי לקבל
כדי לקבל 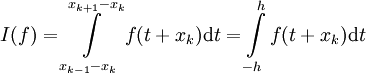 . ניצור פונקציה
. ניצור פונקציה 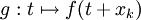 ונבנה
ונבנה 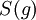 ב-
ב-![[-h,h]](/images/math/0/c/0/0c0f92ce8a45fddea3c69b9d5071ec3d.png) כמו שעשינו בשלב ב:
כמו שעשינו בשלב ב: 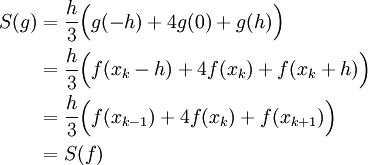
כמו כן, מכיוון ש-
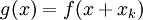 מתקיים
מתקיים ![M=\max_{x\in[-h,h]}\left|g^{(4)}(x)\right|=\max_{x\in[x_{k-1},x_{k+1}]}\left|f^{(4)}(x)\right|](/images/math/5/1/9/51971dc66f119a79a8a2ce3333a6f041.png) , ומכל זה נובע
, ומכל זה נובע ![I_{[x_{k-1},x_{k+1}]}(f)-S_{[x_{k-1},x_{k+1}]}(f)=I_{[-h,h]}(g)-S_{[-h,h]}(g)\le\frac2{45}Mh^5](/images/math/3/c/1/3c134890d348bfe30de30e93832a1e23.png) .
.
סיכום
מצאנו שעל כל תת קטע
![[x_{k-1},x_{k+1}]](/images/math/8/a/4/8a43f36d9e8f2ce9259f885a5e87cad7.png) הטעות בקירוב סימפסון חסומה ע"י
הטעות בקירוב סימפסון חסומה ע"י 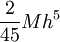 . יש
. יש 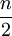 קטעים כאלה, ומכיוון ש-
קטעים כאלה, ומכיוון ש-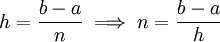 הטעות חסומה ע"י
הטעות חסומה ע"י 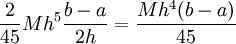 .
.
הערה: ניתן להוכיח כי הטעות חסומה גם ע"י
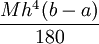 .
.
- נניח ש-f אינטגרבילית ואי-זוגית בקטע סימטרי