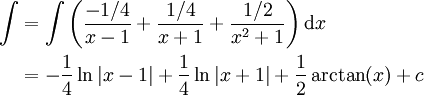משתמש:אור שחף/133 - הרצאה/8.3.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
תוכן עניינים
שיטות אינטגרציה
דוגמאות
בכל אחת מהדוגמאות הבאות נסמן את האינטגרל שיש לחשב כ-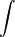 .
.
-
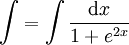 : נציב
: נציב 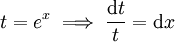 ולכן
ולכן 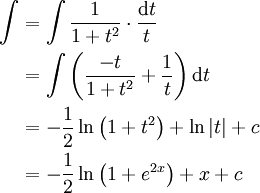

דרך אחרת: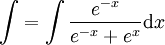 , נציב
, נציב 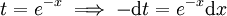 ולכן
ולכן 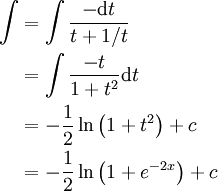

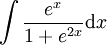 : נגדיר
: נגדיר 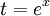 ולכן
ולכן 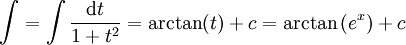 .
. 
-
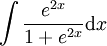 : נגדיר
: נגדיר 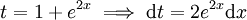 ואז
ואז 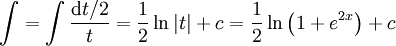 .
. 
-
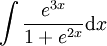 : נציב
: נציב 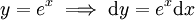 לקבל
לקבל 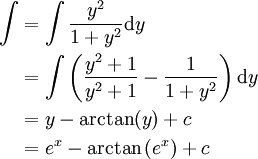

-
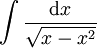 :
: 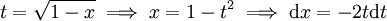 . לפיכך
. לפיכך 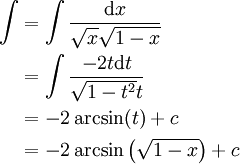

-
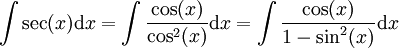 :
: 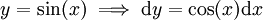 ומכאן נובע
ומכאן נובע 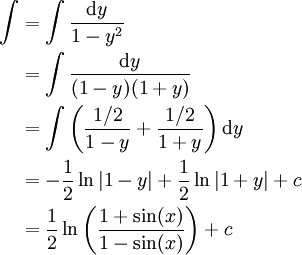

-
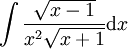 : אם
: אם 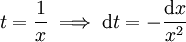 אז נציב
אז נציב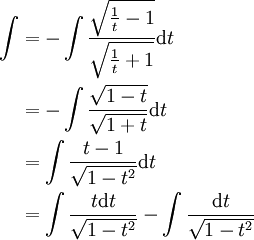
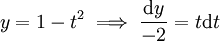 ואז
ואז 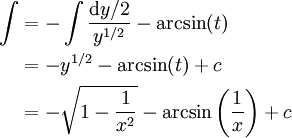

- נתון
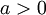 קבוע וצריך למצוא נוסחת נסיגה ל-
קבוע וצריך למצוא נוסחת נסיגה ל-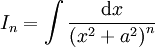 לכל
לכל 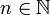 . ברור כי
. ברור כי 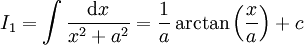 . כעת
. כעת 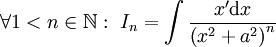 . לפיכך לכן
. לפיכך לכן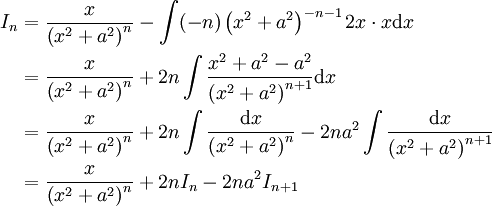
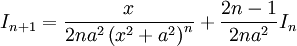 .
.  למשל, עבור
למשל, עבור 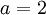 נחשב
נחשב 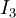 :
: 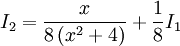 וכן
וכן 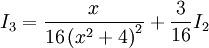 . לבסוף:
. לבסוף: 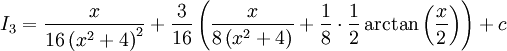 .
. 
שברים חלקיים
נפתח שיטה לביצוע אינטגרציה של פונקציה רציונלית כלשהי 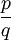 (
(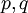 פולינומים). כבר ראינו דוגמה פרטית של השיטה, כאשר פירקנו פונקציה רציונלית לסכום של פונקציות רציונליות פשוטות, וזה יסוד השיטה.
פולינומים). כבר ראינו דוגמה פרטית של השיטה, כאשר פירקנו פונקציה רציונלית לסכום של פונקציות רציונליות פשוטות, וזה יסוד השיטה.
נסתמך ללא הוכחה על משפט מאלגברה: כל פונקציה רציונלית 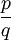 כך ש-
כך ש-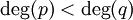 ניתנת לפירוק יחיד כסכום של שברים חלקיים:
ניתנת לפירוק יחיד כסכום של שברים חלקיים: 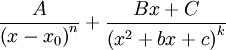 , כאשר
, כאשר 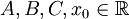 קבועים ולמכנה
קבועים ולמכנה 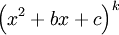 אין שורשים ממשיים (כלומר
אין שורשים ממשיים (כלומר 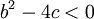 ).
האינטגרציה של השבר הראשון קלה:
).
האינטגרציה של השבר הראשון קלה: 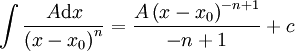 . לשבר השני יותר קשה למצוא אינטגרל. ניתן כמה דוגמאות:
. לשבר השני יותר קשה למצוא אינטגרל. ניתן כמה דוגמאות:
-
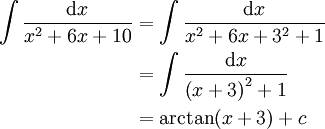
-
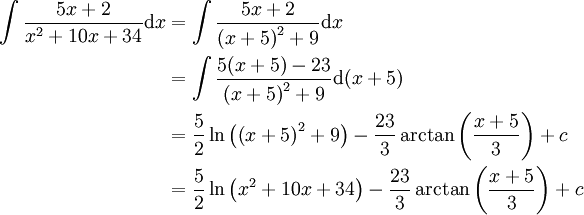 כאשר
כאשר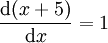 ולכן
ולכן 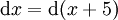 .
. -
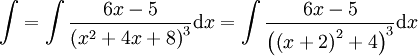 נציב
נציב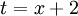 ואז
ואז 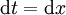 :
: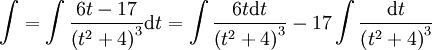 נציב
נציב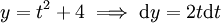 ונסמן
ונסמן 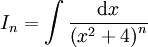 :
: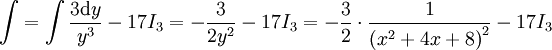 כאשר
כאשר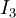 הוא בדיוק אותו
הוא בדיוק אותו 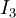 שמצאנו בסעיף 8 בדוגמאות מקודם.
שמצאנו בסעיף 8 בדוגמאות מקודם.
באופן כללי נהפוך את השבר ל-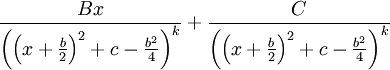 . את האינטגרל של השבר השמאלי (זה שבמונהו יש
. את האינטגרל של השבר השמאלי (זה שבמונהו יש 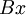 ) נחשב ע"י הצבת
) נחשב ע"י הצבת 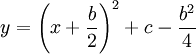 , ואת השבר הימני לפי סעיף 8 בדוגמאות הנ"ל. לחלופין, את שני השברים הללו אפשר לחשב לפי שברים חלקיים.
, ואת השבר הימני לפי סעיף 8 בדוגמאות הנ"ל. לחלופין, את שני השברים הללו אפשר לחשב לפי שברים חלקיים.
![p(x)=\sum_{k=0}^n a_kx^k\in\mathbb R_n[x]](/images/math/9/2/3/9232048210562f7110c61b9bfb69e2fa.png) אז קיים לו פירוק
אז קיים לו פירוק 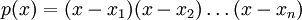 (כאשר
(כאשר 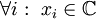 ). חלק מה-
). חלק מה-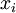 -ים יכולים להיות ממשיים, אבל בכל אופן מספר השורשים הלא ממשיים יהא זוגי. למשל:
-ים יכולים להיות ממשיים, אבל בכל אופן מספר השורשים הלא ממשיים יהא זוגי. למשל: ![\begin{align}\Big(x-(a+bi)\Big)\Big(x-(a-bi)\Big)&=x^2-(a+bi+a-bi)x+(a+bi)(a-bi)\\&=x^2-2ax+\left(a^2+b^2\right)\\&\in\mathbb R_2[x]\end{align}](/images/math/6/1/a/61a1f23c5b1a056a2e1341e70fad4927.png)
כעת, בהינתן האינטגרל 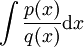 כאשר
כאשר 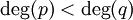 נפרק את
נפרק את 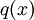 ל-
ל-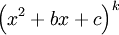 ו-
ו-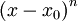 כנ"ל, נמצא
כנ"ל, נמצא 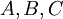 כנזכר למעלה ונחשב את האינטגרל.
כנזכר למעלה ונחשב את האינטגרל.
דוגמאות
-
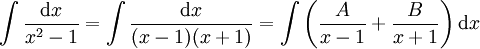 . A ו-B מקיימים ונקבל
. A ו-B מקיימים ונקבל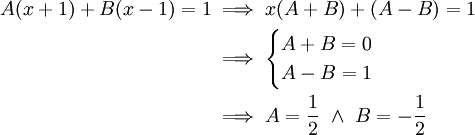
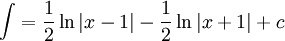 .
. -
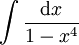 : האינטגרנד שווה ל-
: האינטגרנד שווה ל-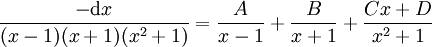 . נמצא את A,B,C,D: מתקיים
. נמצא את A,B,C,D: מתקיים 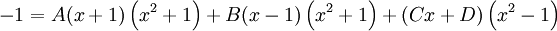 .
.
נציב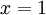 ואז
ואז 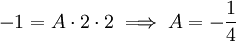 .
.
נציב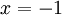 :
:  .
.
נציב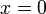 ונקבל
ונקבל 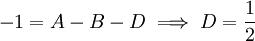 .
.
לבסוף נציב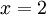 ואז
ואז 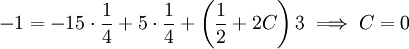 .
.
לפיכך