הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/13.3.11"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(יצירת דף עם התוכן "=שיטות אינטגרציה {{הערה|(המשך)}}= ==דוגמה 0== פתור <math>\int e^\sqrt x\mathrm dx</math>. ===פתרון=== נשתמש בשיטת הה...")
 
שורה 3: שורה 3:
 
פתור <math>\int e^\sqrt x\mathrm dx</math>.
 
פתור <math>\int e^\sqrt x\mathrm dx</math>.
 
===פתרון===
 
===פתרון===
−
נשתמש בשיטת ההצבה (כי אנו יודעים לפתור את האינטגרל <math>\int e^y\mathrm dy</math>).
+
נשתמש בשיטת ההצבה:
 
{|
 
{|
 
{{=|l=\int e^\sqrt x\mathrm dx
 
{{=|l=\int e^\sqrt x\mathrm dx
שורה 30: שורה 30:
 
   |r=\frac12\int\frac{2x-4+4}{x^2-4x+8}\mathrm dx
 
   |r=\frac12\int\frac{2x-4+4}{x^2-4x+8}\mathrm dx
 
}}
 
}}
−
{{=|r=\frac12\int\frac{2x-4}{x^2-4x+8}+2\int\frac1{x^2-4x+8}\mathrm dx
+
{{=|r=\frac12\int\frac{2x-4}{x^2-4x+8}\mathrm dx+2\int\frac1{x^2-4x+8}\mathrm dx
 
}}
 
}}
 
{{=|r=\frac12\ln\vert x^2-4x+8\vert+\int\frac{\mathrm dx}{(x-2)^2+4}
 
{{=|r=\frac12\ln\vert x^2-4x+8\vert+\int\frac{\mathrm dx}{(x-2)^2+4}
 
   |c=כאשר המכנה הוא פולינום אי פריק נכוון ל-<math>\arctan</math> (<math>\int\frac{\mathrm dx}{x^2+1}</math>):
 
   |c=כאשר המכנה הוא פולינום אי פריק נכוון ל-<math>\arctan</math> (<math>\int\frac{\mathrm dx}{x^2+1}</math>):
 +
}}
 
{{=|r=\frac12\ln\vert x^2-4x+8\vert+\frac12\arctan\left(\frac{x-2}2\right)+c
 
{{=|r=\frac12\ln\vert x^2-4x+8\vert+\frac12\arctan\left(\frac{x-2}2\right)+c
−
   |c=לפי הנוסחה <math>\int\frac{\mathrm dx}{a^2+x^2}=\frac1a\arctan\left(\frac xa\right)</math>
+
   |c=לפי הנוסחה <math>\int\frac{\mathrm dx}{a^2+x^2}=\frac1a\arctan\left(\frac xa\right)+c</math>
 
}}
 
}}
 
|}
 
|}
שורה 49: שורה 50:
 
נמצא <math>\int\frac{2x+4}{x^3-2x^2}\mathrm dx</math>.
 
נמצא <math>\int\frac{2x+4}{x^3-2x^2}\mathrm dx</math>.
 
====פתרון====
 
====פתרון====
−
<math>x^3-2x^2=x^2(x-2)</math> ולכן נחשב <math>\int\frac{-2x(x-2)-1(x-2)+2x^2}{x^2(x-2)}\mathrm dx=-2\int\frac{\mathrm dx}x-\int\frac{\mathrm dx}{x^2}+2\int\frac{\mathrm dx}{x-2}=-2\ln|x|+\frac2x+2\ln|x-2|+c</math>. {{משל}}
+
<math>x^3-2x^2=x^2(x-2)</math> ולכן נחשב <math>\int\frac{-2x(x-2)-2(x-2)+2x^2}{x^2(x-2)}\mathrm dx=-2\int\frac{\mathrm dx}x-\int\frac{2\mathrm dx}{x^2}+2\int\frac{\mathrm dx}{x-2}=-2\ln|x|+\frac2x+2\ln|x-2|+c</math>. {{משל}}
 
===דוגמה 4===
 
===דוגמה 4===
 
נחשב <math>\int\frac{x^2+x-2}{3x^3-x^2+3x-1}\mathrm dx</math>.
 
נחשב <math>\int\frac{x^2+x-2}{3x^3-x^2+3x-1}\mathrm dx</math>.

גרסה מ־16:59, 13 במרץ 2011

שיטות אינטגרציה (המשך)

דוגמה 0

פתור 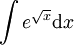\int e^\sqrt x\mathrm dx.

פתרון

נשתמש בשיטת ההצבה:

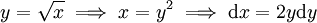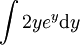
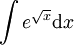
נציב y=\sqrt x\implies x=y^2\implies \mathrm dx=2y\mathrm dy ולכן: \int 2ye^y\mathrm dy = \int e^\sqrt x\mathrm dx
אינטגרציה בחלקים: 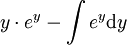y\cdot e^y-\int e^y\mathrm dy =
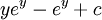
y e^y-e^y+c =
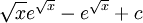
\sqrt x e^\sqrt x-e^\sqrt x+c =

\blacksquare

אינטגרלים של פונקציות רציונליות

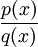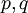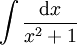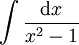נמצא אינטגרלים לפונקציות מהצורה \frac{p(x)}{q(x)} כאשר p,q פולינומים. למשל, האינטגרלים \int\frac{\mathrm dx}{x^2+1} ו-\int\frac{\mathrm dx}{x^2-1}. פתרון שני האינטגרלים יכול להיות שונה כי האינטגרל הראשון אי-פריק ב-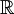\mathbb R, בעוד שהשני כן פריק.

דוגמה 1

נפתור 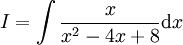I=\int\frac x{x^2-4x+8}\mathrm dx.

נפתור

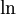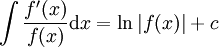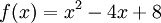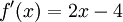באופן כללי, אם מעלת המונה היא n ומעלת המכנה היא n+1 נכוון ל-\ln (כי \int\frac{f'(x)}{f(x)}\mathrm dx=\ln|f(x)|+c. ואכן, אם f(x)=x^2-4x+8 אז f'(x)=2x-4. נשנה את המונה כך שיהיה f'(x):

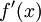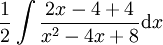
\frac12\int\frac{2x-4+4}{x^2-4x+8}\mathrm dx = I
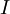
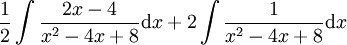
\frac12\int\frac{2x-4}{x^2-4x+8}\mathrm dx+2\int\frac1{x^2-4x+8}\mathrm dx =
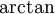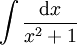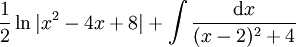
כאשר המכנה הוא פולינום אי פריק נכוון ל-\arctan (\int\frac{\mathrm dx}{x^2+1}): \frac12\ln\vert x^2-4x+8\vert+\int\frac{\mathrm dx}{(x-2)^2+4} =
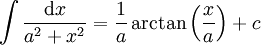
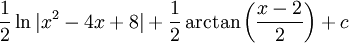
לפי הנוסחה \int\frac{\mathrm dx}{a^2+x^2}=\frac1a\arctan\left(\frac xa\right)+c \frac12\ln\vert x^2-4x+8\vert+\frac12\arctan\left(\frac{x-2}2\right)+c =

\blacksquare

לעומת זאת, אם המכנה הוא פולינום פריק (ואנו יודעים לפרק אותו) ניתן להשתמש בשיטת "פירוק לשברים" שמטרתה להוריד את דרגת המכנה - מחפשים A,B שיקיימו 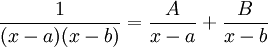\frac1{(x-a)(x-b)}=\frac A{x-a}+\frac B{x-b}.

דוגמה 2

נחשב 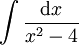\int\frac{\mathrm dx}{x^2-4}.

פתרון

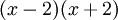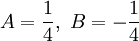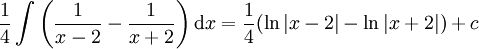קל לראות שהמכנה פריק ושווה ל-(x-2)(x+2). עתה מחפשים A,B כנ"ל ומקבלים A=\frac14,\ B=-\frac14. לכן האינטגרל הוא \frac14\int\left(\frac1{x-2}-\frac1{x+2}\right)\mathrm dx=\frac14(\ln|x-2|-\ln|x+2|)+c. \blacksquare

דוגמה 3

נמצא 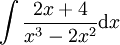\int\frac{2x+4}{x^3-2x^2}\mathrm dx.

פתרון

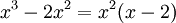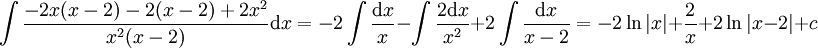x^3-2x^2=x^2(x-2) ולכן נחשב \int\frac{-2x(x-2)-2(x-2)+2x^2}{x^2(x-2)}\mathrm dx=-2\int\frac{\mathrm dx}x-\int\frac{2\mathrm dx}{x^2}+2\int\frac{\mathrm dx}{x-2}=-2\ln|x|+\frac2x+2\ln|x-2|+c. \blacksquare

דוגמה 4

נחשב 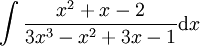\int\frac{x^2+x-2}{3x^3-x^2+3x-1}\mathrm dx.

פתרון

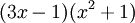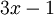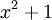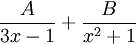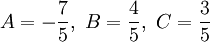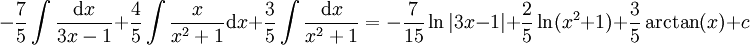אפשר לראות שהמכנה שווה ל-(3x-1)(x^2+1). ברור כי עבור 3x-1 השורש הוא 0, בעוד של-x^2+1 אין שורשים ממשיים. לכן יש למצוא A,B עבורם האינטגרל הוא \frac A{3x-1}+\frac B{x^2+1}. נקבל A=-\frac75,\ B=\frac45,\ C=\frac35 ולכן האינטגרל הוא -\frac75\int\frac{\mathrm dx}{3x-1}+\frac45\int\frac x{x^2+1}\mathrm dx+\frac35\int\frac{\mathrm dx}{x^2+1}=-\frac7{15}\ln|3x-1|+\frac25\ln(x^2+1)+\frac35\arctan(x)+c. \blacksquare

כלל: כאשר הפונקציה רציונלית ומעלת המונה גדולה מהמכנה נפנה לחילוק פולינומים.

דוגמה 5

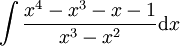
\int\frac{x^4-x^3-x-1}{x^3-x^2}\mathrm dx

פתרון

נחלק:

עיבוד הנוסחה נכשל (שגיאת תחביר): \begin{align}\overset{x}{\overline{x^4&-x^3&-x&-1}|x^3-x^2}\\\underline{x^4&-x^3}\\&&-x&-1\end{align}

ולכן יש לפתור את האינטגרל עיבוד הנוסחה נכשל (שגיאת תחביר): \int\left(x-\frac{x+1}{x^3-x^2}\right)\mathrm dx=\int x\mathrm dx-\int\frac{-2x(x-1)-x(x-1)+2x^2}{x^2(x-1)}\mathrm dx=\frac{x^2}2-\int\frac{2\mathrm dx}x^2}-\int\frac{\mathrm dx}{x^2}+\int\frac{2\mathrm dx}{x-1}=-2\ln|x|+\frac1x+2\ln|x-1|+c

מקור: https://math-wiki.com/index.php?title=משתמש:אור_שחף/133_-_תרגול/13.3.11&oldid=10082