משתמש:אור שחף/133 - תרגול/15.5.11
תוכן עניינים
התכנסות במ"ש (המשך)
משפט: 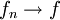 במ"ש בקטע I אם"ם לכל
במ"ש בקטע I אם"ם לכל 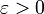 יש
יש 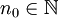 כך שלכל
כך שלכל 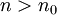 מתקיים
מתקיים 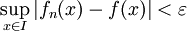 .
.
דוגמה 1
תהי 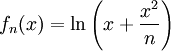 . קבעו התכנסות בכל אחד מהקטעים הבאים:
. קבעו התכנסות בכל אחד מהקטעים הבאים:
-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) עבור
עבור 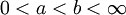
- בקטע
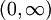
פתרון
פונקציית הגבול היא 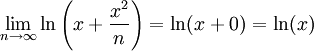 .
.
- נראה התכנסות במ"ש ב-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: ![\sup_{x\in[a,b]}\left|\ln\left(x+\frac{x^2}n\right)-\ln(x)\right|=\sup_{n\in[a,b]}\left|\ln\left(1+\frac xn\right)\right|=\ln\left(1+\frac bn\right)\to0](/images/math/7/8/e/78eadb924b5606b53c77b6fd652d1f9c.png) .
. 
- נראה שההתכנסות נקודתית בלבד ב-
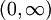 :
: 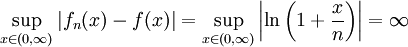 .
. 
דוגמה 2
קבע האם 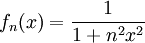 מתכנסת במ"ש ב-
מתכנסת במ"ש ב-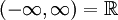 .
.
פתרון
קל לראות ש-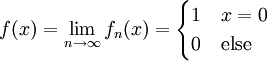 . נבדוק התכנסות במ"ש:
. נבדוק התכנסות במ"ש: 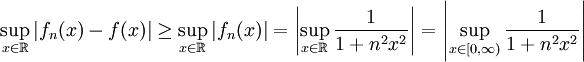 . נחפש מקסימום:
. נחפש מקסימום: 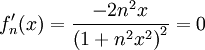 וקל לראות שהנגזרת מתאפסת עבור
וקל לראות שהנגזרת מתאפסת עבור 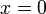 . ברור ש-
. ברור ש-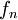 מונוטונית יורדת ב-
מונוטונית יורדת ב-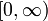 ולכן זו אכן נקודת מקסימום גלובלית. מתקיים
ולכן זו אכן נקודת מקסימום גלובלית. מתקיים 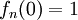 ולכן
ולכן 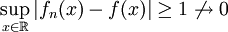 . מכאן שההתכנסות נקודתית בלבד.
. מכאן שההתכנסות נקודתית בלבד. 
דוגמה 3
תהי  סדרת פונקציות המתכנסת במ"ש לפונקציה f, האם f חסומה?
סדרת פונקציות המתכנסת במ"ש לפונקציה f, האם f חסומה?
פתרון
נבחר לדוגמה 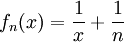 בקטע
בקטע 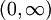 . ברור כי
. ברור כי 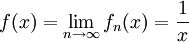 וכי אם
וכי אם 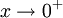 אז
אז 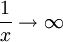 , לכן f לא חסומה.
, לכן f לא חסומה. 
דוגמה 4
תהי 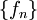 סדרת פונקציות המתכנסת לפונקציה f במ"ש ב-I. נוכיח כי אם כל אחת מהפונקציות
סדרת פונקציות המתכנסת לפונקציה f במ"ש ב-I. נוכיח כי אם כל אחת מהפונקציות 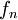 חסומה ב-I, אזי גם f חסומה ב-I.
חסומה ב-I, אזי גם f חסומה ב-I.
פתרון
נרשום 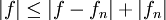 . נתון כי ההתכנסות במ"ש ולכן
. נתון כי ההתכנסות במ"ש ולכן 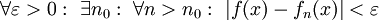 , בפרט עבור
, בפרט עבור 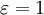 . כמו כן
. כמו כן 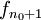 חסומה ב-I (מהנתון) כלומר קיים M כך ש-
חסומה ב-I (מהנתון) כלומר קיים M כך ש-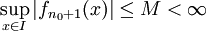 ולכן מתקבל ש-
ולכן מתקבל ש-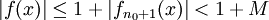 לכל
לכל 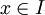 .
. 
משפט: אם 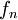 מתכנסת במ"ש בקטע I וכל
מתכנסת במ"ש בקטע I וכל 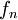 רציפה אזי f רציפה.
רציפה אזי f רציפה.
דוגמה 5
ניתן דוגמה לסדרת פונקציות רציפות המתכנסות לפונקציה רציפה אבל לא מתכנסת במ"ש.
פתרון
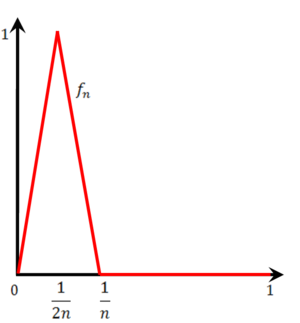
נגדיר את הפונקציה הבאה: 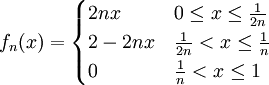 . קל לראות שהפונקציה הנ"ל מוגדרת בקטע
. קל לראות שהפונקציה הנ"ל מוגדרת בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , אפשר לראות שהפונקציה הנ"ל רציפה.
, אפשר לראות שהפונקציה הנ"ל רציפה.
לכל 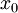 יש
יש 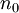 כך שלכל
כך שלכל 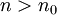 מתקיים
מתקיים 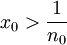 שם מתקיים
שם מתקיים 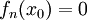 , כלומר
, כלומר 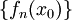 סדרה קבועה מ-
סדרה קבועה מ-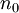 מסויים. כמו כן
מסויים. כמו כן ![\sup_{x\in[0,1]}|f_n(x)-f(x)|=1](/images/math/3/8/8/38831bf7034d433905af6c64706a862c.png) ולכן ההתכנסות אינה במ"ש.
ולכן ההתכנסות אינה במ"ש.
טורים של פונקציות
דוגמה 6
נסמן לכל n, 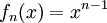 בקטע
בקטע 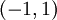 . מה היא פונקצית הסכום
. מה היא פונקצית הסכום 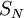 ?
?
פתרון
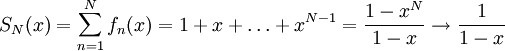 .
.
דוגמה 7
נוכיח כי הטור 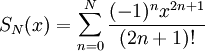 מתכנס ל-
מתכנס ל-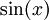 במ"ש בקטע
במ"ש בקטע ![[0,2\pi]](/images/math/5/8/c/58c9a5de0cb1a343ae0acd1fb191eea1.png) כאשר
כאשר 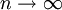 .
.
פתרון
בזכות טורי טיילור ברור שיש התכנסות נקודתית, נותר לבדוק התכנסות במ"ש. נסמן 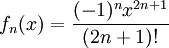 . כאשר
. כאשר 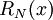 השארית בין הטור-טיילור מסדר N לבין
השארית בין הטור-טיילור מסדר N לבין 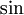 מתקיים
מתקיים 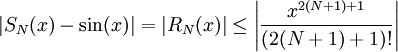 . כמו כן
. כמו כן 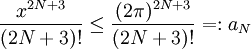 . נוכיח ש-
. נוכיח ש-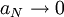 וכך נוכיח שההתכנסות במ"ש. מספיק להסתכל על
וכך נוכיח שההתכנסות במ"ש. מספיק להסתכל על 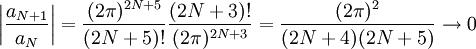 , לכן
, לכן 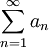 מתכנס ובפרט
מתכנס ובפרט 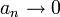 .
. 
דוגמה 8
בדקו התכנסות במ"ש של 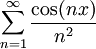 .
.
פתרון
נשים לב כי לא ידועה לנו פונקצית הגבול של הטור ולכן לא ניתן להוכיח התכנסות במ"ש ישירות מההגדרה. במקום, נפנה לתנאי קושי: יהי 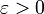 נתון. ברור כי
נתון. ברור כי 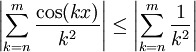 . הטור
. הטור 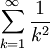 מתכנס ולכן מקיים את תנאי קושי, כלומר קיים
מתכנס ולכן מקיים את תנאי קושי, כלומר קיים 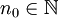 כל שלכל
כל שלכל 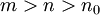 מתקיים
מתקיים 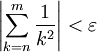 . לכן, עבור אותו
. לכן, עבור אותו 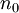 , לכל
, לכל 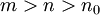 מתקיים
מתקיים 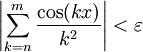 .
.