משתמש:אור שחף/133 - תרגול/27.2.11
תוכן עניינים
אינטגרל לפי רימן
הגדרה: יהי ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) קטע סגור. נסמן את
קטע סגור. נסמן את ![T_{[a,b]}](/images/math/0/a/4/0a4e5263cf494a93e9e6f146278ffe75.png) כחלוקה
כחלוקה 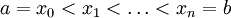 ונקרא ל-T חלוקה. נסמן
ונקרא ל-T חלוקה. נסמן 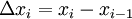 כאשר
כאשר 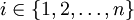 .
.
הגדרה: תהי f פונקציה המוגדרת ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ותהי T חלוקה של הקטע. עבור כל תת קטע
ותהי T חלוקה של הקטע. עבור כל תת קטע ![[x_{i-1},x_i]](/images/math/c/d/4/cd4ecc36c89db79c632a849e2e8a2adc.png) נבחר נקודה
נבחר נקודה ![\alpha_i\in[x_{i-1},x_i]](/images/math/4/9/8/498f7954b41ed72838fd61e12e6b8250.png) ונבנה סכום מהצורה
ונבנה סכום מהצורה 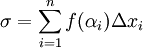 . סכום זה נקרא סכום רימן של f והוא תלוי ב-
. סכום זה נקרא סכום רימן של f והוא תלוי ב-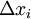 וב-
וב-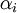 .
.
הגדרה: פרמטר החלוקה של T מוגדר כ-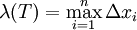 .
.
הגדרה: תהי 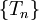 סדרת חלוקות של הקטע
סדרת חלוקות של הקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נאמר כי
. נאמר כי 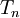 נורמלית אם
נורמלית אם 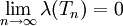 .
.
הגדרה: נאמר כי סכומי רימן שואפים לגבול I כאשר 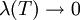 אם לכל
אם לכל 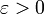 קיימת
קיימת 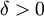 כך שלכל חלוקה T עבורה
כך שלכל חלוקה T עבורה 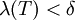 מתקיים
מתקיים 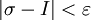 .
.
דוגמה 1
נמצא פונקציה לא אינטגרבילית. דוגמה קלאסית לכך היא פונקצית דיריכלה - לכל חלוקה נורמלית שנבחר תהיה נקודה רציונלית ונקודה אי-רציונלית בתת קטע ![[x_{i-1},x_i]](/images/math/c/d/4/cd4ecc36c89db79c632a849e2e8a2adc.png) של
של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ולכן סכום רימן יכול להיות כל ערך בין 0 ל-
ולכן סכום רימן יכול להיות כל ערך בין 0 ל-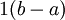 (כולל).
(כולל).
דוגמה 2
קבע אינטגרביליות של f בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) כאשר
כאשר 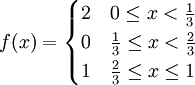 .
.
פתרון
נוכיח אינטגרביליות לפי רימן. תהי 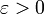 נתונה. צריך להוכיח כי קיימת
נתונה. צריך להוכיח כי קיימת 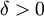 כך שלכל חלוקה T, עבורה
כך שלכל חלוקה T, עבורה 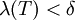 מתקיים
מתקיים 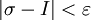 . נצייר את הפונקציה:
. נצייר את הפונקציה:
גרף (1)
אינטואיטיבית, מהגרף ניתן לראות שהשטח מתחת ל-f הוא 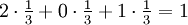 , כלומר אנו ננסה להוכיח ש-
, כלומר אנו ננסה להוכיח ש-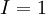 :
:
נסמן ב-T את החלוקה 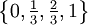 של
של ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) . נבחר
. נבחר 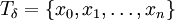 העדנה של T המקיימת
העדנה של T המקיימת 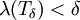 ונבנה את סכום רימן באופן הבא:
תהי
ונבנה את סכום רימן באופן הבא:
תהי 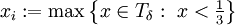 ותהי
ותהי 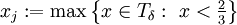 . עבור
. עבור 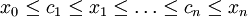 , סכומי רימן הם
, סכומי רימן הם
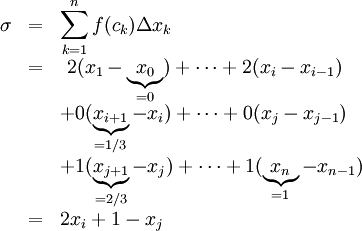
נשים לב כי 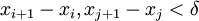 ולכן
ולכן 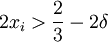 ו-
ו-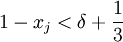 . כמו כן, לפי הגדרת
. כמו כן, לפי הגדרת 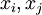 , מתקיים
, מתקיים 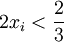 ו-
ו-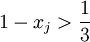 . מכאן ש-
. מכאן ש-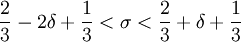 . נזכיר כי חשדנו ש-
. נזכיר כי חשדנו ש-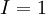 ולכן נבדוק מהו
ולכן נבדוק מהו 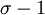 :
:
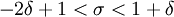 ולכן
ולכן 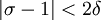 . נבחר
. נבחר 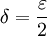 ונקבל את הדרוש. לסיכום, ערך האינטגרל הוא 1 ובוודאי ש-f אינטגרבילית.
ונקבל את הדרוש. לסיכום, ערך האינטגרל הוא 1 ובוודאי ש-f אינטגרבילית. 
דוגמה 3
חשב את הגבול ![\lim_{n\to\infty}\sqrt[n]{\left(1+\frac1n\right)\left(1+\frac2n\right)\dots\left(1+\frac nn\right)}](/images/math/9/0/f/90fb116162dd2c45f5dabc2368d3ebcb.png) .
.
פתרון
נתבונן בסדרה 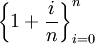 . כאשר
. כאשר 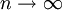 , קל לראות שמדובר בקטע
, קל לראות שמדובר בקטע ![[1,2]](/images/math/f/7/9/f79408e5ca998cd53faf44af31e6eb45.png) . לפי חוקי לוגריתמים אפשר לרשום:
. לפי חוקי לוגריתמים אפשר לרשום: ![\lim_{n\to\infty} \ln\sqrt[n]{\prod_{i=1}^n\left(1+\frac in\right)}=\lim_{n\to\infty} \frac1n \ln \prod_{i=1}^n\left(1+\frac in\right)=\lim_{n\to\infty}\frac1n \sum_{i=1}^n\ln\left(1+\frac in\right)](/images/math/d/5/0/d50826b74d627b0a09276e695b7e93e6.png) . ברור כי ln אינטגרבילית ב-
. ברור כי ln אינטגרבילית ב-![(1,2]](/images/math/8/2/a/82a2d3646998b80552965f9919d183c5.png) ולכן נבחר חלוקה שעבורה
ולכן נבחר חלוקה שעבורה 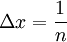 , ואז
, ואז 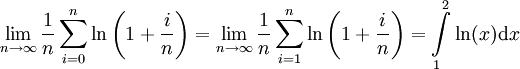 .
.
הערה: את האינטגרל הזה נלמד לפתור בשיעור הבא.
משפט: אם 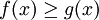 ו-f ו-g אינטגרביליות אז
ו-f ו-g אינטגרביליות אז 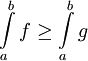 .
.
דוגמה 4
קבע האם האינטגרל הנתון בעל ערך חיובי או שלילי: 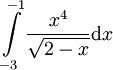 .
.
פתרון
נסמן 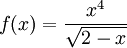 קל לראות ש-f חיובית בקטע
קל לראות ש-f חיובית בקטע ![[-3,-1]](/images/math/2/f/7/2f7fd20f37f46e40fbcd80e723eee1c4.png) ולכן
ולכן 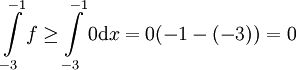 , כלומר אי-שלילי. נעיר ש-
, כלומר אי-שלילי. נעיר ש-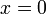 (שהיא הנקודה המאפסת היחידה של f ב-
(שהיא הנקודה המאפסת היחידה של f ב-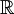 ) אינה בקטע ולכן התוצאה חיובית.
) אינה בקטע ולכן התוצאה חיובית. 
דוגמה 5
נוכיח כי 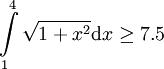 .
.
פתרון
נתון כי  ולכן
ולכן  . מכאן ש-
. מכאן ש-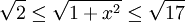 חיובית. נפעיל אינטגרל (צריכים רק את צד שמאל) ונקבל
חיובית. נפעיל אינטגרל (צריכים רק את צד שמאל) ונקבל ![\int\limits_1^4 f\ge\int\limits_1^4\sqrt2\mathrm dx=\left[\sqrt2x\right]_{x=1}^4=\sqrt2\cdot4-\sqrt2=3\sqrt2](/images/math/6/0/1/601752ca3f8fa983b4437b6a09b7eac7.png) . התוצאה קטנה מ-7.5 ולכן נחפש חסם אחר:
. התוצאה קטנה מ-7.5 ולכן נחפש חסם אחר: 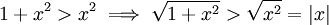 , לכן
, לכן ![\int\limits_1^4 f>\int\limits_1^4|x|\mathrm dx=\int\limits_1^4 x\mathrm dx=\left[\frac{x^2}2\right]_{x=1}^4=7.5](/images/math/b/7/a/b7a83347c5296b58e1ea75ec91361bc5.png) .
. 
דוגמה 6
הוכח כי ![\frac2{\sqrt[4]e}\le\int\limits_0^2 e^{x^2-x}\mathrm dx\le2e^2](/images/math/c/2/a/c2aa53a3348fc468a006e70f68ad4d46.png)
פתרון
ננסה למצוא קבועים המקיימים 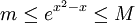 (כי אינטגרל של קבוע אנו יודעים לפתור).
נמצא מינימום ומקסימום. נסמן
(כי אינטגרל של קבוע אנו יודעים לפתור).
נמצא מינימום ומקסימום. נסמן 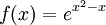 ואז
ואז 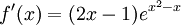 ולכן נקודה החשודה כקיצון היא
ולכן נקודה החשודה כקיצון היא 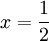 :
: 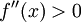 ולפיכך היא מינימום. לפי וירשטרס נחפש גם בקצוות:
ולפיכך היא מינימום. לפי וירשטרס נחפש גם בקצוות: 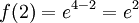 (מקסימום) וכן
(מקסימום) וכן 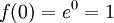 . לכן
. לכן 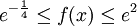 . לפיכך
. לפיכך 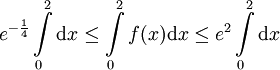 ונקבל בדיוק את מה שרשום.
ונקבל בדיוק את מה שרשום. 