תוכן עניינים

1 טורי חזקות (המשך)

טורי חזקות (המשך)

דוגמה 1

חשבו את רדיוס ההתכנסות של הטור 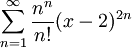$\sum_{n=1}^\infty\frac{n^n}{n!}(x-2)^{2n}$ .

פתרון

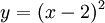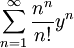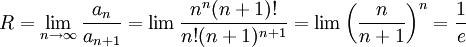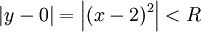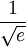נתחיל מההצבה $y=(x-2)^2$ כדי שנקבל תבנית של טור חזקות: $\sum_{n=1}^\infty\frac{n^n}{n!}y^n$ . נעזר במבחן המנה: $R=\lim_{n\to\infty} \frac{a_n}{a_{n+1}}=\lim \frac{n^n(n+1)!}{n!(n+1)^{n+1}}=\lim\left(\frac n{n+1}\right)^n=\frac1e$ , כלומר רדיוס ההתכנסות של הטור החדש הוא $\frac1e$ ולכן רדיוס ההתכנסות של הטור המקורי (מכיוון ש- $|y-0|=\left|(x-2)^2\right|<R$ ) הוא $\frac1\sqrt e$ . $\blacksquare$

דוגמה 2

מצאו את תחום ההתכנסות של הטור 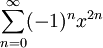$\sum_{n=0}^\infty (-1)^nx^{2n}$ וחשבו את סכומו לכל x בתחום.

פתרון

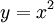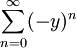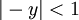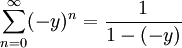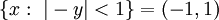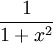אם נציב $y=x^2$ נקבל את הטור ההנדסי $\sum_{n=0}^\infty (-y)^n$ . טור זה מתכנס אם"ם $|-y|<1$ ואם כן אזי $\sum_{n=0}^\infty (-y)^n=\frac1{1-(-y)}$ . לסיכום, תחום ההתכנסות הוא $\{x:\ |-y|<1\}=(-1,1)$ וסכום הטור הוא $\frac1{1+x^2}$ . $\blacksquare$

דוגמה 3

הוכח כי 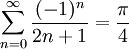$\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}=\frac\pi4$ .

פתרון

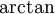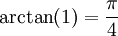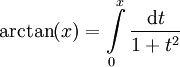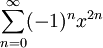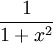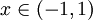נכוון לטור טיילור של $\arctan$ כי $\arctan(1)=\frac\pi4$ . ידוע כי $\arctan(x)=\int\limits_0^x\frac{\mathrm dt}{1+t^2}$ , ומכיוון ש- $\sum_{n=0}^\infty (-1)^nx^{2n}$ מתכנס במ"ש על $[0,x]$ ל- $\frac1{1+x^2}$ לכל $x\in(-1,1)$ אפשר לעשות אינטגרציה איבר-איבר: 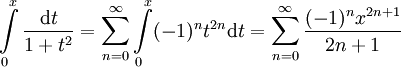$\int\limits_0^x\frac{\mathrm dt}{1+t^2}=\sum_{n=0}^\infty\int\limits_0^x (-1)^nt^{2n}\mathrm dt=\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1}$ . הנקודה 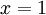$x=1$ אמנם אינה נמצאת ב- 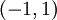$(-1,1)$ , אבל אפשר להשתמש במבחן אבל: אם לטור 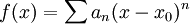$f(x)=\sum a_n(x-x_0)^n$ יש רדיוס התכנסות R ו- 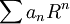$\sum a_nR^n$ מתכנס ל-S אזי 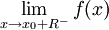$\lim_{x\to x_0+R^-}f(x)$ קיים ושווה ל-S. 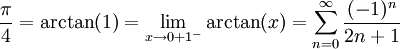לפיכך $\frac\pi4=\arctan(1)=\lim_{x\to0+1^-}\arctan(x)=\sum_{n=0}^\infty \frac{(-1)^n}{2n+1}$ . $\blacksquare$

דוגמה 4

חשבו 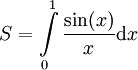$S=\int\limits_0^1\frac{\sin(x)}x\mathrm dx$ בקירוב של $10^{-6}$ .

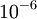פתרון

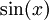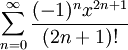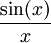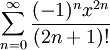טור טיילור של $\sin(x)$ הוא $\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{(2n+1)!}$ ולכן טור טיילור של $\frac{\sin(x)}x$ הוא $\sum_{n=0}^\infty\frac{(-1)^nx^{2n}}{(2n+1)!}$ . ברור כי הטור הנ"ל מתכנס במ"ש בכל 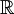$\mathbb R$ (כי רדיוס ההתכנסות הוא, עפ"י מבחן השורש או מבחן המנה, 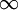$\infty$ ) ולכן נעשה אינטגרציה איבר-איבר: 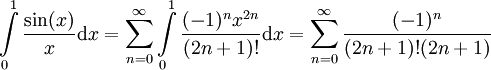$\int\limits_0^1\frac{\sin(x)}x\mathrm dx=\sum_{n=0}^\infty\int\limits_0^1 \frac{(-1)^nx^{2n}}{(2n+1)!}\mathrm dx=\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)!(2n+1)}$ . הטור באגף הימיני ביותר הוא טור לייבניץ ולכן (מאינפי 1) 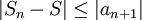$|S_n-S|\le|a_{n+1}|$ (כאשר S הוא סכום הטור, 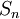$S_n$ הוא סכום הטור החלקי מהאיבר ה-0 עד n, ו- 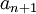$a_{n+1}$ הוא האיבר ה- 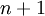$n+1$ של הטור). 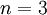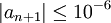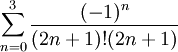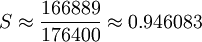עבור $n=3$ מתקיים $|a_{n+1}|\le 10^{-6}$ ולכן נחשב $\sum_{n=0}^3\frac{(-1)^n}{(2n+1)!(2n+1)}$ , ונקבל $S\approx\frac{166889}{176400}\approx 0.946083$ . $\blacksquare$

דוגמה 5

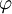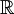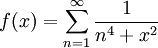נתונה פונקציה $\varphi$ רציפה כלשהי ב- $\mathbb R$ והפונציה $f(x)=\sum_{n=1}^\infty\frac1{n^4+x^2}$ .

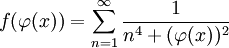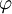הוכיחו כי הטור $f(\varphi(x))=\sum_{n=1}^\infty\frac1{n^4+(\varphi(x))^2}$ מתכנס במ"ש בתחום ההגדרה של $\varphi$ .
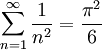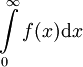העזרו בכך ש- $\sum_{n=1}^\infty\frac1{n^2}=\frac{\pi^2}6$ (אין צורך להוכיח זאת) וחשבו את $\int\limits_0^\infty f(x)\mathrm dx$ .

פתרון

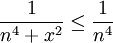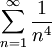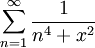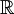נעזר במבחן ה-M של ויירשראס: $\frac1{n^4+x^2}\le\frac1{n^4}$ ו- $\sum_{n=1}^\infty\frac1{n^4}$ מתכנס, לכן הטור $\sum_{n=1}^\infty\frac1{n^4+x^2}$ מתכנס במ"ש על $\mathbb R$ .
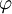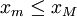טענת עזר: נוכיח שהטווח של $\varphi$ הוא קטע. ראשית נוכיח שלכל קטע $[a,b]$ , $\mbox{Im}(\varphi|_{[a,b]})$ הוא קטע. ממשפט ויירשראס השני, קיימת נקודה $x_M\in[a,b]$ שבה $\varphi|_{[a,b]}$ מקסימלית ו- $x_m\in[a,b]$ שבה היא מינימלית, ונניח בלי הגבלת הכלליות ש- $x_m\le x_M$ . 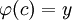אזי $\varphi|_{[a,b]}$ רציפה ב- $[x_m,x_M]$ ולכן, מממשפט ערך הביניים, לכל $y\in[\varphi(x_m),\varphi(x_M)]$ קיים $c\in[x_m,x_M]$ כך ש- $\varphi(c)=y$ . 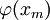לפיכך הוכחנו ש- $\mbox{Im}(\varphi|_{[a,b]})\supseteq[\varphi(x_m),\varphi(x_M)]$ . 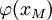מאידך, $\varphi(x_m)$ הוא הערך המינימלי של $\varphi|_{[a,b]}$ ו- $\varphi(x_M)$ הוא הערך המקסימלי, לכן ברור ש- $\mbox{Im}(\varphi|_{[a,b]})\subseteq[\varphi(x_m),\varphi(x_M)]$ . מכאן ש- $\mbox{Im}(\varphi|_{[a,b]})=[\varphi(x_m),\varphi(x_M)]$ , כלומר הטווח הוא קטע, כדרוש. 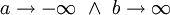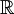הטענה נכונה לכל קטע $[a,b]$ ולכן נשאיף $a\to-\infty\ \and\ b\to\infty$ ונקבל שהיא נכונה ל- $\mathbb R$ .
לפיכך מתקיימים התנאים לשימוש במבחן ה-M של ויירשראס, ומכיוון שהטור של f מתכנסת במ"ש על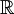 $\mathbb R$ הוא בפרט מתכנס במ"ש על תת הקטע 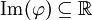$\mbox{Im}(\varphi)\subseteq\mathbb R$ . מכאן ש- 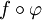$f\circ\varphi$ מתכנס במ"ש. $\blacksquare$
הטור מתכנס במ"ש ולכן ניתן לעשות אינטגרציה איבר-איבר:
$\begin{align}\int\limits_0^\infty f&=\sum_{n=1}^\infty\int\limits_0^\infty\frac{\mathrm dx}{n^4+x^2}\\&=\sum_{n=1}^\infty\frac1{n^4}\int\limits_0^\infty\frac{\mathrm dx}{1+\left(\frac x{n^2}\right)^2}\\&=\sum_{n=1}^\infty\left[\frac1{n^2}\arctan\left(\frac xn\right)\right]_{x=0}^\infty\\&=\sum_{n=1}^\infty \frac1{n^2}\frac\pi2\\&=\frac{\pi^3}{12}\end{align}$
$\blacksquare$

דוגמה 6

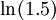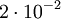קרבו את $\ln(1.5)$ כך שהשארית קטנה מ- $2\cdot10^{-2}$ .

פתרון

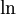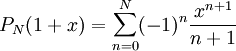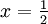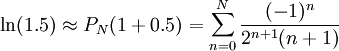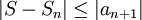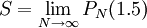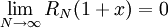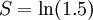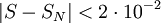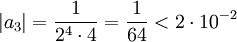נעזר בטור טיילור מסדר N של $\ln$ : $P_N(1+x)=\sum_{n=0}^N (-1)^n\frac{x^{n+1}}{n+1}$ ונציב $x=\tfrac12$ . קיבלנו $\ln(1.5)\approx P_N(1+0.5)=\sum_{n=0}^N\frac{(-1)^n}{2^{n+1}(n+1)}$ , שהוא טור לייבניץ ולכן $|S-S_n|\le|a_{n+1}|$ (כאשר $S=\lim_{N\to\infty}P_N(1.5)$ , ומכיוון שכבר הוכחנו בעבר ש- $\lim_{N\to\infty}R_N(1+x)=0$ נקבל $S=\ln(1.5)$ ). 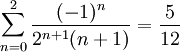דרוש ש- $|S-S_N|<2\cdot10^{-2}$ , ובגלל ש- $|a_3|=\frac1{2^4\cdot4}=\frac1{64}<2\cdot10^{-2}$ נחשב $\sum_{n=0}^2\frac{(-1)^n}{2^{n+1}(n+1)}=\frac5{12}$ . $\blacksquare$