הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"
איתמר שטיין (שיחה | תרומות) |
איתמר שטיין (שיחה | תרומות) |
||
| שורה 21: | שורה 21: | ||
\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & 0 & 3 \end{bmatrix} | \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & 0 & 3 \end{bmatrix} | ||
</math> | </math> | ||
| + | |||
<math> | <math> | ||
| שורה 53: | שורה 54: | ||
(זאת לא התשובה היחידה הנכונה, אבל זאת אחת הפשוטות) | (זאת לא התשובה היחידה הנכונה, אבל זאת אחת הפשוטות) | ||
| + | |||
| + | |||
| + | שאלה 2: | ||
| + | נתונה מערכת המיוצגת על ידי המטריצה | ||
| + | <math>\begin{bmatrix} 1 & a_1 & a_2 & 0 & a_3 & | & 0 \\ a_4 & 0 & a_5 & 2 & a_6 & | & 0 \\ a_7 & 0 & a_8 & 0 & a_9 & | & 0 | ||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | סעיף א) אם המטריצה מדורגת זה אומר ש <math>a_4 = a_7 = 0</math> כי שתיהם נמצאים מתחת לאיבר מוביל של השורה הראשונה. | ||
| + | |||
| + | בנוסף אפשר לראות ש <math>a_8=0</math>. הוכחה: נניח בשלילה ש <math>a_8 \neq 0</math>. | ||
| + | |||
| + | אם <math>a_5 \neq 0</math> הוא נמצא מתחת לאיבר מוביל של השורה השניה. | ||
| + | |||
| + | אם <math>a_5 = 0</math> הוא יהיה איבר מוביל משמאל לאיבר המוביל של השורה השניה. | ||
| + | |||
| + | לכן <math>a_8=0</math>. | ||
| + | |||
| + | לגבי שאר הפרמטרים, כל בחירה שהיא שלהם תשאיר את המטריצה מדורגת ולכן לא ניתן לדעת מהם. | ||
| + | |||
| + | סעיף ב) אם <math>A</math> מדורגת קנונית אז <math>2</math> לא יכול להיות איבר מוביל של השורה השניה. | ||
| + | |||
| + | לכן, <math>a_5 \neq 0</math> כלומר הוא איבר מוביל ולכן <math>a_5 = 1</math>. | ||
| + | |||
| + | בנוסף <math>a_2 = 0</math> כי הוא מעל האיבר המוביל של השורה השניה. | ||
| + | |||
| + | את הפרמטר <math>a_1</math> אי אפשר לקבוע. | ||
| + | גם את הפרמטרים <math>a_3,a_6,a_9</math> לא ניתן עדיין לקבוע בוודאות. כי יכול להיות ש <math>a_9=0</math> ואז <math>a_3,a_6</math> יכולים להיות כל מספר שהוא. | ||
| + | |||
| + | ויכול להיות ש <math>a_9=1</math> (ואז <math>a_3=a_6=0</math>). | ||
| + | |||
| + | סעיף ג) אם נתון שיש שני משתנים חופשיים, אז יש שלושה איברים מובילים ולכן | ||
| + | |||
| + | <math>a_9=1</math> ולכן <math>a_3=a_6=0</math> כי הם מעל איבר מוביל של השורה השלישית. | ||
| + | |||
| + | את <math>a_1</math> עדיין לא ניתן לקבוע. | ||
| + | |||
| + | |||
| + | לכן קיבלנו | ||
| + | |||
| + | <math>\begin{bmatrix} 1 & a_1 & 0 & 0 & 0 & | & 0 \\ 0 & 0 & 1 & 2 & 0 & | & 0 \\ 0 & 0 & 0 & 0 & 1 & | & 0 | ||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | סעיף ד) פתרון פשוט של המערכת מוביל ל | ||
| + | |||
| + | <math>x_5 = 0</math> | ||
| + | <math>x_4 = t</math> | ||
| + | <math>x_3=-2t</math> | ||
| + | <math>x_2 = s</math> | ||
| + | <math>x_1 = -a_1s</math> | ||
| + | |||
| + | כלומר | ||
| + | |||
| + | <math>(-a_1s,s,-2t,t,0)</math>. | ||
גרסה מ־14:55, 28 באוגוסט 2012
פתרון הבוחן:
שאלה 1:
נתון כי 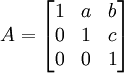 .
ו
.
ו 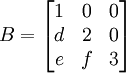 .
.
צריך למצוא מטריצות אלמנטריות 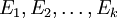 . כך ש
. כך ש 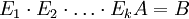 .
.
מדרגים את מטריצה  למטריצה
למטריצה  .
.
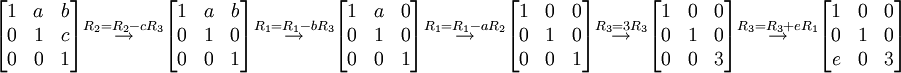
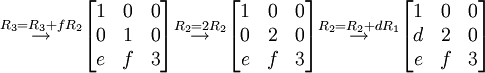
לכן מטריצות אלמנטריות מתאימות הן
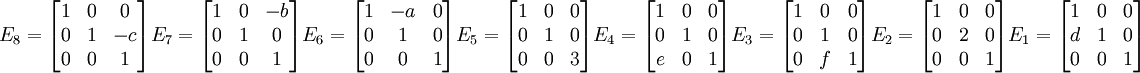
ומתקיים 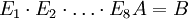 .
.
(זאת לא התשובה היחידה הנכונה, אבל זאת אחת הפשוטות)
שאלה 2:
נתונה מערכת המיוצגת על ידי המטריצה
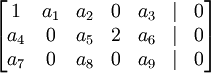
סעיף א) אם המטריצה מדורגת זה אומר ש 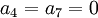 כי שתיהם נמצאים מתחת לאיבר מוביל של השורה הראשונה.
כי שתיהם נמצאים מתחת לאיבר מוביל של השורה הראשונה.
בנוסף אפשר לראות ש 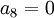 . הוכחה: נניח בשלילה ש
. הוכחה: נניח בשלילה ש 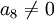 .
.
אם 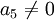 הוא נמצא מתחת לאיבר מוביל של השורה השניה.
הוא נמצא מתחת לאיבר מוביל של השורה השניה.
אם 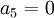 הוא יהיה איבר מוביל משמאל לאיבר המוביל של השורה השניה.
הוא יהיה איבר מוביל משמאל לאיבר המוביל של השורה השניה.
לכן 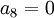 .
.
לגבי שאר הפרמטרים, כל בחירה שהיא שלהם תשאיר את המטריצה מדורגת ולכן לא ניתן לדעת מהם.
סעיף ב) אם  מדורגת קנונית אז
מדורגת קנונית אז 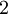 לא יכול להיות איבר מוביל של השורה השניה.
לא יכול להיות איבר מוביל של השורה השניה.
לכן, 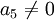 כלומר הוא איבר מוביל ולכן
כלומר הוא איבר מוביל ולכן 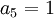 .
.
בנוסף 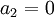 כי הוא מעל האיבר המוביל של השורה השניה.
כי הוא מעל האיבר המוביל של השורה השניה.
את הפרמטר 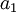 אי אפשר לקבוע.
גם את הפרמטרים
אי אפשר לקבוע.
גם את הפרמטרים 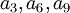 לא ניתן עדיין לקבוע בוודאות. כי יכול להיות ש
לא ניתן עדיין לקבוע בוודאות. כי יכול להיות ש 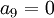 ואז
ואז 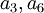 יכולים להיות כל מספר שהוא.
יכולים להיות כל מספר שהוא.
ויכול להיות ש 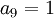 (ואז
(ואז 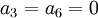 ).
).
סעיף ג) אם נתון שיש שני משתנים חופשיים, אז יש שלושה איברים מובילים ולכן
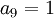 ולכן
ולכן 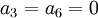 כי הם מעל איבר מוביל של השורה השלישית.
כי הם מעל איבר מוביל של השורה השלישית.
את 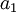 עדיין לא ניתן לקבוע.
עדיין לא ניתן לקבוע.
לכן קיבלנו
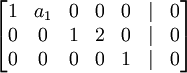
סעיף ד) פתרון פשוט של המערכת מוביל ל
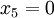
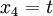
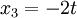
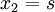
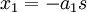
כלומר
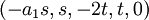 .
.