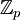|
|
| שורה 1: |
שורה 1: |
| | *[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]] | | *[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]] |
| − |
| |
| − |
| |
| − | ==שאלה 2==
| |
| − |
| |
| − | ===סעיף א===
| |
| − |
| |
| − | טענת עזר: אם <math>A,B</math> קבוצות חסומות מלעיל אז
| |
| − |
| |
| − |
| |
| − | <math>\sup(A+B)=\sup(A)+\sup(B)</math>
| |
| − |
| |
| − |
| |
| − | הוכחה: נוכיח שהמספר <math>\sup(A)+\sup(B)</math> מקיים את התכונות של <math>\sup(A+B)</math>
| |
| − |
| |
| − | * תכונה א': חסם מלעיל של <math>A+B</math>. הוכחה:
| |
| − |
| |
| − |
| |
| − | אם <math>x\in A+B</math> אז ניתן לכתוב <math>x=a+b</math> כאשר <math>a\in A, b\in B</math>.
| |
| − |
| |
| − | היות ו <math>a\leq \sup(A)</math> ו <math>b\leq \sup(B)</math> מתקיים
| |
| − |
| |
| − | <math>x=a+b\leq \sup(A)+\sup(B)</math>
| |
| − |
| |
| − |
| |
| − | * תכונה ב': החסם המלעיל הכי קטן. הוכחה:
| |
| − |
| |
| − | יהי <math>y</math> איזשהוא חסם מלעיל של <math>A+B</math>
| |
| − |
| |
| − | נניח בשלילה ש <math>y<\sup(A)+\sup(B)</math>
| |
| − |
| |
| − | אז נקבל ש <math>y-\sup(B)<\sup(A)</math>
| |
| − |
| |
| − | ולכן קיים <math>a\in A</math> כך ש <math>y-\sup(B)<a</math>
| |
| − |
| |
| − | מכאן נקבל <math>y-a<\sup(B)</math>
| |
| − |
| |
| − | ולכן קיים <math>b\in B</math> כך ש <math>y-a<b</math>
| |
| − |
| |
| − | ולכן <math>y<a+b\in A+B</math>
| |
| − |
| |
| − | בסתירה לכך ש <math>y</math> חסם מלעיל של <math>A+B</math>
| |
| − |
| |
| − | לכן בהכרח מתקיים <math>\sup(A)+\sup(B)\leq y</math>
| |
| − |
| |
| − | לסיכום: הוכחנו שהמספר <math>\sup(A)+\sup(B)</math> מקיים את שתי התכונות של חסם עליון
| |
| − |
| |
| − | ולכן <math>\sup(A+B)=\sup(A)+\sup(B)</math>. מש"ל טענת עזר.
| |
| − |
| |
| − | עכשיו קל להוכיח את הדרוש:
| |
| − |
| |
| − | <math>\sup(A+B+C)=\sup(A+B)+\sup(C)=\sup(A)+\sup(B)+\sup(C)</math>
| |
| − |
| |
| − | מש"ל.
| |
| − |
| |
| − | ===סעיף ב===
| |
| − |
| |
| − | הפרכה פשוטה, ניקח <math>a_n=-\frac{1}{n}</math> ו <math>b_n=\frac{1}{n}</math>
| |
| − |
| |
| − | מתקיים שלכל <math>n\in \mathbb{N}</math>
| |
| − | <math>a_n<b_n</math>
| |
| − | (ולכן בוודאי שזה מקיים כמעט לכל <math>n\in \mathbb{N}</math>).
| |
| − |
| |
| − | אבל
| |
| − |
| |
| − | <math>\lim_{n\rightarrow \infty}a_n=\lim_{n\rightarrow \infty}b_n=0</math>
| |
| − |
| |
| − |
| |
| − | שתי הערות:
| |
| − | א) כמעט לכל <math>n</math> פירושו: לכל <math>n</math> פרט למספר סופי של מקרים.
| |
| − |
| |
| − | אן לחילופין: קיים <math>N\in \mathbb{N}</math> כך שהטענה מתקיימת לכל <math>n>N</math>.
| |
| − |
| |
| − | ב) כמובן שהטענה הבאה נכונה
| |
| − |
| |
| − | אם <math>a_n\leq b_n</math> ו
| |
| − |
| |
| − | <math>\lim_{n\rightarrow \infty}a_n=a,\quad \lim_{n\rightarrow \infty}b_n=b</math>
| |
| − |
| |
| − | אז
| |
| − |
| |
| − | <math>a\leq b</math>.
| |