הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"
מתוך Math-Wiki
איתמר שטיין (שיחה | תרומות) (←סעיף ב) |
איתמר שטיין (שיחה | תרומות) (←שאלה 5) |
||
| שורה 2: | שורה 2: | ||
| − | == | + | ===סעיף ב=== |
| + | נשים לב ש | ||
| + | |||
| + | <math>\frac{1}{n} \sum_{i=1}^n f(x_i)</math> | ||
| + | |||
| + | זה ממוצע של הערכים | ||
| + | |||
| + | <math>f(x_1),\ldots , f(x_n)</math> | ||
| + | |||
| + | מבין הערכים האלה חייב להיות מינימום ומקסימום. | ||
| + | |||
| + | כלומר קיימים <math>i_0,i_1</math> עבורם | ||
| + | |||
| + | <math>f(x_{i_0})=\min\{f(x_1),\ldots , f(x_n)\},\quad f(x_{i_1})=\max\{f(x_1),\ldots , f(x_n)\}</math> | ||
| + | |||
| + | ואז נקבל | ||
| + | |||
| + | <math>\frac{1}{n} \sum_{i=1}^n f(x_i)\leq \frac{1}{n} \sum_{i=1}^n f(x_{i_1}) = f(x_{i_1})</math> | ||
| + | |||
| + | ובאופן דומה | ||
| + | |||
| + | <math>\frac{1}{n} \sum_{i=1}^n f(x_i)\geq \frac{1}{n} \sum_{i=1}^n f(x_{i_0}) = f(x_{i_0})</math> | ||
| + | |||
| + | נניח בלי הגבלת כלליות ש | ||
| + | <math>x_{i_0}<x_{i_1}</math> | ||
| + | |||
| + | ראינו שהערך | ||
| + | <math>\sum_{i=1}^n f(x_i)</math> | ||
| + | |||
| + | נמצא בין <math>f(x_{i_0})</math> ל <math>f(x_{i_1})</math> | ||
| + | |||
| + | וברור ש <math>f</math> | ||
| + | רציפה על | ||
| + | <math>[x_{i_0},x_{i_1}]</math> | ||
| + | |||
| + | לכן לפי משפט ערך הביניים קיים | ||
| + | |||
| + | <math>c\in (x_{i_0},x_{i_2})\subseteq (a,b)</math> | ||
| + | |||
| + | כך ש: | ||
| + | |||
| + | <math>f(c)=\sum_{i=1}^n f(x_i)</math> | ||
| + | |||
| + | וזה מראה את מה שנדרש | ||
גרסה מ־06:38, 1 בפברואר 2013
סעיף ב
נשים לב ש
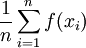
זה ממוצע של הערכים
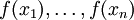
מבין הערכים האלה חייב להיות מינימום ומקסימום.
כלומר קיימים 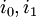 עבורם
עבורם

ואז נקבל
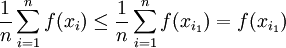
ובאופן דומה
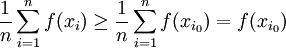
נניח בלי הגבלת כלליות ש
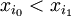
ראינו שהערך
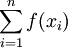
נמצא בין 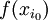 ל
ל 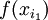
וברור ש  רציפה על
רציפה על
![[x_{i_0},x_{i_1}]](/images/math/d/e/c/decf35065e8fca080ef3bb8107d8f8f5.png)
לכן לפי משפט ערך הביניים קיים
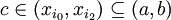
כך ש:
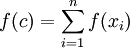
וזה מראה את מה שנדרש