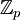הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏סעיף ב)
שורה 1: שורה 1:
 +
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
 +
 +
 +
==שאלה 1==
 +
 +
===סעיף א===
 +
 +
עבור נקודות <math>(x,y,z)\neq (0,0,0)</math> פשוט גוזרים את הפונקציה לפי <math>x</math>
 +
 +
<math>f_x(x,y,z)=\frac{zy\cos(xy){(x^2+y^2+z^2)}^\frac{1}{3}-\frac{1}{3}{(x^2+y^2+z^2)}^{-\frac{2}{3}}\cdot (2x)\cdot{(z\sin(xy))}}{{(x^2+y^2+z^2)}^\frac{2}{3}}</math>
 +
 +
 +
עבור הנקודה <math>(x,y,z)=(0,0,0)</math> קל לראות ש
 +
 +
<math>\lim_{t\rightarrow 0}\frac{f(t,0,0)-f(0,0,0)}{t}=\lim_{t\rightarrow 0}\frac{0-0}{t}=0</math>
 +
 +
 
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
 
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
  
שורה 38: שורה 55:
 
מתכנסת ל <math>0</math> בנקודה <math>(0,0,0)</math>.
 
מתכנסת ל <math>0</math> בנקודה <math>(0,0,0)</math>.
  
−
במקרה שלנו צריך:
+
במקרה שלנו צריך לבדוק את:
 +
 
 +
<math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3\sin (h_1 h_2)}{{(h_1^2+h_2^2+h_3^2)}^\frac{1}{3}\cdot {(h_1^2+h_2^2+h_3^2)}^{\frac{1}{2}}}
 +
= \lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}\frac{\sin(h_1 h_2)}{h_1 h_2}
 +
</math>
 +
 
 +
היות ו
 +
 
 +
<math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)} \frac{\sin(h_1 h_2)}{h_1 h_2} = 1</math>
 +
 
 +
נותר לבדוק את
 +
 
 +
<math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}</math>
 +
 
 +
נשים לב ש
 +
 
 +
<math>|\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}|\leq |\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2)}^\frac{5}{6}}|
 +
\leq |h_3||\frac{h_1 h_2}{{(2h_1 h_2)}^\frac{5}{6}}|= |h_3||{(h_1 h_2)}^{\frac{1}{6}}|\rightarrow 0
 +
</math>
  
−
<math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}</math>
+
דרך אחרת:

גרסה מ־18:52, 3 בפברואר 2013


שאלה 1

סעיף א

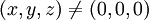עבור נקודות (x,y,z)\neq (0,0,0) פשוט גוזרים את הפונקציה לפי x

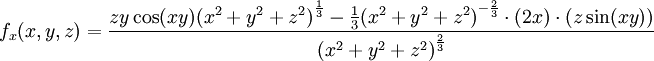
f_x(x,y,z)=\frac{zy\cos(xy){(x^2+y^2+z^2)}^\frac{1}{3}-\frac{1}{3}{(x^2+y^2+z^2)}^{-\frac{2}{3}}\cdot (2x)\cdot{(z\sin(xy))}}{{(x^2+y^2+z^2)}^\frac{2}{3}}


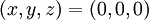עבור הנקודה (x,y,z)=(0,0,0) קל לראות ש

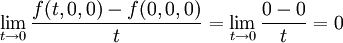
\lim_{t\rightarrow 0}\frac{f(t,0,0)-f(0,0,0)}{t}=\lim_{t\rightarrow 0}\frac{0-0}{t}=0



שאלה 1

סעיף א

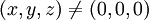עבור נקודות (x,y,z)\neq (0,0,0) פשוט גוזרים את הפונקציה לפי x

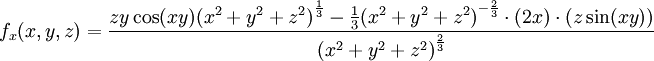
f_x(x,y,z)=\frac{zy\cos(xy){(x^2+y^2+z^2)}^\frac{1}{3}-\frac{1}{3}{(x^2+y^2+z^2)}^{-\frac{2}{3}}\cdot (2x)\cdot{(z\sin(xy))}}{{(x^2+y^2+z^2)}^\frac{2}{3}}


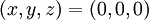עבור הנקודה (x,y,z)=(0,0,0) קל לראות ש

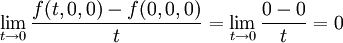
\lim_{t\rightarrow 0}\frac{f(t,0,0)-f(0,0,0)}{t}=\lim_{t\rightarrow 0}\frac{0-0}{t}=0


סעיף ב

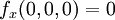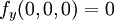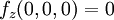כמו שראינו בקלות ש f_x(0,0,0)=0 קל לראות שגם f_y(0,0,0)=0 ו f_z(0,0,0)=0.

ראשית נוודא ש f רציפה (לא חייבים, אבל בדר"כ שווה לבדוק. כי אם היא לא רציפה אז ברור שהיא לא דיפרנציאבילית).

נשים לב ש

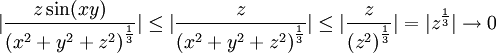
|\frac{z\sin(xy)}{{(x^2+y^2+z^2)}^{\frac{1}{3}}}|\leq |\frac{z}{{(x^2+y^2+z^2)}^{\frac{1}{3}}}|\leq |\frac{z}{{(z^2)}^{\frac{1}{3}}}|=|z^{\frac{1}{3}}|\rightarrow 0

ולכן f רציפה.

נבדוק דיפרנציאביליות

צריך לבדוק אם 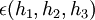\epsilon (h_1,h_2,h_3) המוגדרת לפי:

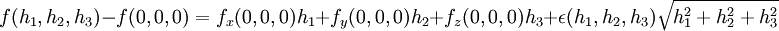
f(h_1,h_2,h_3)-f(0,0,0)=f_x(0,0,0)h_1+f_y(0,0,0)h_2+f_z(0,0,0)h_3+\epsilon(h_1,h_2,h_3)\sqrt{h_1^2+h_2^2+h_3^2}

מתכנסת ל 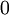0 בנקודה (0,0,0).

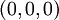במקרה שלנו צריך לבדוק את:

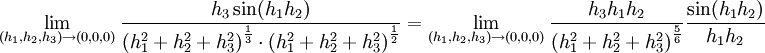
\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3\sin (h_1 h_2)}{{(h_1^2+h_2^2+h_3^2)}^\frac{1}{3}\cdot {(h_1^2+h_2^2+h_3^2)}^{\frac{1}{2}}} = \lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}\frac{\sin(h_1 h_2)}{h_1 h_2}

היות ו

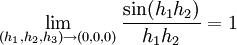
\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)} \frac{\sin(h_1 h_2)}{h_1 h_2} = 1

נותר לבדוק את

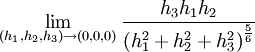
\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}

נשים לב ש

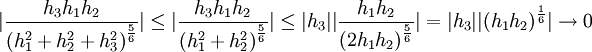
|\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}|\leq |\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2)}^\frac{5}{6}}| \leq |h_3||\frac{h_1 h_2}{{(2h_1 h_2)}^\frac{5}{6}}|= |h_3||{(h_1 h_2)}^{\frac{1}{6}}|\rightarrow 0

דרך אחרת:

מקור: https://math-wiki.com/index.php?title=משתמש:איתמר_שטיין&oldid=32059