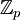|
|
| שורה 1: |
שורה 1: |
| | *[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]] | | *[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]] |
| − |
| |
| − | ==שאלה 1==
| |
| − |
| |
| − | ===סעיף א===
| |
| − |
| |
| − | עבור נקודות <math>(x,y,z)\neq (0,0,0)</math> פשוט גוזרים את הפונקציה לפי <math>x</math>
| |
| − |
| |
| − | <math>f_x(x,y,z)=\frac{zy\cos(xy){(x^2+y^2+z^2)}^\frac{1}{3}-\frac{1}{3}{(x^2+y^2+z^2)}^{-\frac{2}{3}}\cdot (2x)\cdot{(z\sin(xy))}}{{(x^2+y^2+z^2)}^\frac{2}{3}}</math>
| |
| − |
| |
| − |
| |
| − | עבור הנקודה <math>(x,y,z)=(0,0,0)</math> קל לראות ש
| |
| − |
| |
| − | <math>\lim_{t\rightarrow 0}\frac{f(t,0,0)-f(0,0,0)}{t}=\lim_{t\rightarrow 0}\frac{0-0}{t}=0</math>
| |
| − |
| |
| − |
| |
| − | ===סעיף ב===
| |
| − |
| |
| − |
| |
| − | כמו שראינו בקלות ש <math>f_x(0,0,0)=0</math> קל לראות שגם <math>f_y(0,0,0)=0</math> ו <math>f_z(0,0,0)=0</math>.
| |
| − |
| |
| − | ראשית נוודא ש <math>f</math> רציפה (לא חייבים, אבל בדר"כ שווה לבדוק. כי אם היא לא רציפה אז ברור שהיא לא דיפרנציאבילית).
| |
| − |
| |
| − | נשים לב ש
| |
| − |
| |
| − | <math>|\frac{z\sin(xy)}{{(x^2+y^2+z^2)}^{\frac{1}{3}}}|\leq |\frac{z}{{(x^2+y^2+z^2)}^{\frac{1}{3}}}|\leq
| |
| − | |\frac{z}{{(z^2)}^{\frac{1}{3}}}|=|z^{\frac{1}{3}}|\rightarrow 0</math>
| |
| − |
| |
| − | ולכן <math>f</math> רציפה.
| |
| − |
| |
| − | נבדוק דיפרנציאביליות
| |
| − |
| |
| − | צריך לבדוק אם <math>\epsilon (h_1,h_2,h_3)</math> המוגדרת לפי:
| |
| − |
| |
| − | <math>f(h_1,h_2,h_3)-f(0,0,0)=f_x(0,0,0)h_1+f_y(0,0,0)h_2+f_z(0,0,0)h_3+\epsilon(h_1,h_2,h_3)\sqrt{h_1^2+h_2^2+h_3^2}</math>
| |
| − |
| |
| − | מתכנסת ל <math>0</math> בנקודה <math>(0,0,0)</math>.
| |
| − |
| |
| − | במקרה שלנו צריך לבדוק את:
| |
| − |
| |
| − | <math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3\sin (h_1 h_2)}{{(h_1^2+h_2^2+h_3^2)}^\frac{1}{3}\cdot {(h_1^2+h_2^2+h_3^2)}^{\frac{1}{2}}}
| |
| − | = \lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}\frac{\sin(h_1 h_2)}{h_1 h_2}
| |
| − | </math>
| |
| − |
| |
| − | היות ו
| |
| − |
| |
| − | <math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)} \frac{\sin(h_1 h_2)}{h_1 h_2} = 1</math>
| |
| − |
| |
| − | נותר לבדוק את
| |
| − |
| |
| − | <math>\lim_{(h_1,h_2,h_3)\rightarrow (0,0,0)}\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}</math>
| |
| − |
| |
| − | נשים לב ש
| |
| − |
| |
| − | <math>|\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2+h_3^2)}^\frac{5}{6}}|\leq |\frac{h_3 h_1 h_2}{{(h_1^2+h_2^2)}^\frac{5}{6}}|
| |
| − | \leq |h_3||\frac{h_1 h_2}{{(2h_1 h_2)}^\frac{5}{6}}|= \frac{1}{2^{\frac{5}{6}}}|h_3||{(h_1 h_2)}^{\frac{1}{6}}|\rightarrow 0
| |
| − | </math>
| |
| − |
| |
| − | דרך אחרת (שימושית כאשר יש במכנה דברים בסגנון <math>||h||</math>):
| |
| − |
| |
| − | עוברים לקוארדינטות כדוריות
| |
| − |
| |
| − | <math>h_1 = r\cos \theta \sin \varphi,\quad h_2 = r\sin \theta \sin \varphi ,\quad h_3 = r \cos \varphi</math>
| |
| − |
| |
| − | ואז צריך לחשב גבול
| |
| − |
| |
| − | <math>\lim_{r\rightarrow 0}\frac {r^3 \cos \theta \sin \theta \sin ^2 \varphi \cos \varphi}{{(r^2)}^{\frac{5}{6}}}
| |
| − | =\lim_{r\rightarrow 0} {r^{\frac{8}{6}} \cos \theta \sin \theta \sin ^2 \varphi \cos \varphi}=0
| |
| − | </math>
| |
| − |
| |
| − | ולכן <math>f</math> דיפרנציאבילית ב <math>(0,0,0)</math>.
| |