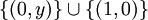הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"
איתמר שטיין (שיחה | תרומות) |
איתמר שטיין (שיחה | תרומות) |
||
| שורה 88: | שורה 88: | ||
כעת נעבור לציר <math>x</math>. | כעת נעבור לציר <math>x</math>. | ||
| + | |||
| + | כלומר נחקור נקודות מהצורה <math>(x_0,0)</math>. | ||
| + | |||
| + | אם <math>x_0>1</math> אז קיימת סביבה של <math>(x_0,0)</math> שבה <math>1-x-y<0</math> ולכן באותה סביבה מתקיים ש | ||
| + | |||
| + | <math>x^3y^2(1-x-y)\leq 0</math> ולכן <math>f(x_0,0)=0</math> היא נקודת מקסימום. | ||
| + | |||
| + | אם <math>0<x_0<1</math> אז קיימת סביבה שבה <math>1-x-y>0</math> ואז <math>x^3y^2(1-x-y)\geq 0</math> ולכן <math>(x_0,0)</math> היא מינימום | ||
| + | |||
| + | אם <math>x<0</math> אז קיימת סביבה שבה <math>1-x-y>0</math> ואז <math>x^3y^2(1-x-y)\leq 0</math> ולכן <math>(x_0,0)</math> היא מקסימום. | ||
| + | |||
| + | כבר ראינו שהנקודה <math>(0,0)</math> היא נקודת אוכף (היא על ציר <math>y</math>). | ||
| + | |||
| + | נותר לבדוק את הנקודה <math>(1,0)</math>. | ||
| + | |||
| + | נתקדם לאורך הישר <math>x=1</math> ונקבל <math>f(1,y)=-y^3</math> שזאת פונקציה עם נקודת פיתול ב <math>y=0</math>. | ||
| + | |||
| + | לכן <math>(1,0)</math> היא נקודת אוכף. | ||
| + | |||
| + | לסיכום: | ||
| + | |||
| + | נקודות קריטיות: | ||
| + | |||
| + | <math>\{(x,y)\mid x=0\}\cup \{(x,y)\mid y=0\} \cup \{(\frac{1}{2},\frac{1}{3})\}</math> | ||
| + | |||
| + | מתוכן: | ||
| + | |||
| + | מקסימום: | ||
| + | |||
| + | <math>\{(\frac{1}{2},\frac{1}{3})\}\cup \{(x,0)\mid x>1 \or x<0\}</math> | ||
| + | |||
| + | מינימום: | ||
| + | |||
| + | <math>\{(x,0)\mid 0<x<1\}</math> | ||
| + | |||
| + | אוכף: | ||
| + | |||
| + | <math>\{(0,y)\}\cup\{(1,0)\}</math> | ||
גרסה מ־07:52, 8 בפברואר 2013
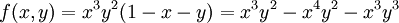
הגרדיאנט הוא:
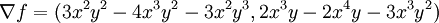
אם נשווה אותו ל 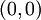 ונקבל:
ונקבל:
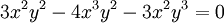
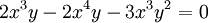
נקבל שאם 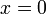 או
או 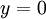 שתי המשוואות מתקיימות.
שתי המשוואות מתקיימות.
אם  , נקבל שהמשוואות הן:
, נקבל שהמשוואות הן:
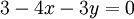
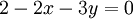
הפתרון של המערכת הזאת הוא:
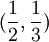
ולכן כלל הנקודות הקריטיות הן:
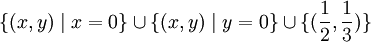
עכשיו צריך לסווג
מטריצת ההסיאן היא:
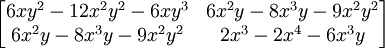
כמובן שהצבה של 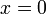 או
או 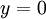 לא תקדם אותנו יותר מדי.
לא תקדם אותנו יותר מדי.
אם נציב 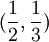 נקבל (אם אין לי טעות חישוב):
נקבל (אם אין לי טעות חישוב):
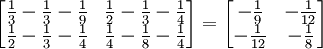
המינור הראשון שלילי והמינור השני חיובי, לכן זו מטריצה שלילית (לחלוטין) ולכן זו נקודת מקסימום.
עכשיו צריך למיין ידנית את שאר הנקודות.
נתחיל בנקודות שעל ציר 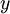 .
.
נביט על נקודה כלשהיא 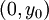 .
.
אם נתקדם לאורך הישר 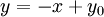 (שעובר כמובן ב
(שעובר כמובן ב 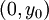 ).
).
אז
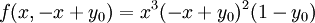
אם 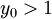 אז הפונקציה שלנו שלילית כש
אז הפונקציה שלנו שלילית כש 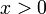 וחיובית כש
וחיובית כש 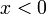
אם 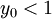 אז הפונקציה שלנו חיובית כש
אז הפונקציה שלנו חיובית כש 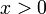 ושלילית כש
ושלילית כש 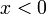
בכל מקרה היא לא תהיה נקודת קיצון.
נותר לבדוק את הנקודה 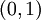 .
.
אם נתקדם לאורך הישר 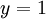 נקבל ש
נקבל ש
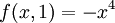 ולכן
ולכן 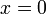 היא מקסימום לאורך הקו הזה.
היא מקסימום לאורך הקו הזה.
אבל אם נתקדם לאורך הישר 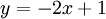 נקבל ש
נקבל ש
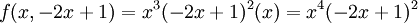 נקבל ש
נקבל ש 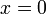 היא נקודת מינימום לאורך הקו הזה.
היא נקודת מינימום לאורך הקו הזה.
לכן 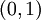 היא גם נקודת אוכף.
היא גם נקודת אוכף.
סיכום ביניים: כל ציר 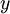 הוא נקודות אוכף.
הוא נקודות אוכף.
כעת נעבור לציר  .
.
כלומר נחקור נקודות מהצורה 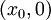 .
.
אם 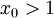 אז קיימת סביבה של
אז קיימת סביבה של 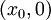 שבה
שבה 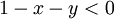 ולכן באותה סביבה מתקיים ש
ולכן באותה סביבה מתקיים ש
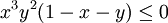 ולכן
ולכן 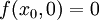 היא נקודת מקסימום.
היא נקודת מקסימום.
אם 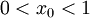 אז קיימת סביבה שבה
אז קיימת סביבה שבה 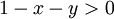 ואז
ואז 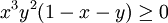 ולכן
ולכן 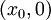 היא מינימום
היא מינימום
אם 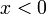 אז קיימת סביבה שבה
אז קיימת סביבה שבה 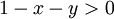 ואז
ואז 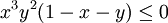 ולכן
ולכן 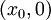 היא מקסימום.
היא מקסימום.
כבר ראינו שהנקודה 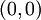 היא נקודת אוכף (היא על ציר
היא נקודת אוכף (היא על ציר 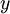 ).
).
נותר לבדוק את הנקודה 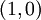 .
.
נתקדם לאורך הישר 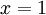 ונקבל
ונקבל 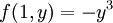 שזאת פונקציה עם נקודת פיתול ב
שזאת פונקציה עם נקודת פיתול ב 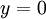 .
.
לכן 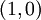 היא נקודת אוכף.
היא נקודת אוכף.
לסיכום:
נקודות קריטיות:
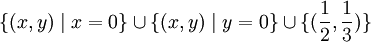
מתוכן:
מקסימום:
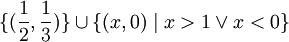
מינימום:
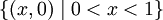
אוכף: