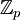הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏שאלה 5)
שורה 1: שורה 1:
−
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
 
−
 
−
 
 
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
 
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
  
שורה 40: שורה 37:
  
 
<math>
 
<math>
 +
= \int _\frac{\pi}{2} ^{\pi} \, \sin(x+\pi) +1 \mathrm{d}x  = -\cos(x+\pi)+x \mid_\frac{\pi}{2} ^{\pi} = -1+\pi - \frac{\pi}{2}
 +
= -1+ \frac{\pi}{2}
 +
</math>
 +
 +
את האינטגרל השני צריך לפצל
 +
 +
<math>
 +
\iint \limits_{\frac{\pi}{2}\leq x+y \leq \frac{3\pi}{2}} \, \cos(x+y) \mathrm{d}x\mathrm{d}y
 
=
 
=
 +
\int _0 ^{\frac{\pi}{2}} \, \int_{\frac{\pi}{2}-x}^{\pi} \, \cos(x+y) \mathrm{d}y\mathrm{d}x+
 +
\int _\frac{\pi}{2} ^{\pi} \, \int_0^{\frac{3\pi}{2}-x} \, \cos(x+y) \mathrm{d}y\mathrm{d}x
 
</math>
 
</math>
 +
 +
<math>
 +
=
 +
\int _0 ^{\frac{\pi}{2}} \, \sin(x+y) \mid_{\frac{\pi}{2}-x}^{\pi} \mathrm{d}x+
 +
\int _\frac{\pi}{2} ^{\pi} \, \sin(x+y) \mid_0^{\frac{3\pi}{2}-x} \mathrm{d}x
 +
=
 +
\int _0 ^{\frac{\pi}{2}} \, \sin(x+\pi) - 1 \mathrm{d}x
 +
\int _\frac{\pi}{2} ^{\pi} \, -1 -\sin(x) \mathrm{d}x
 +
</math>
 +
 +
<math>
 +
=
 +
-\cos(x+\pi) - x \mid_0 ^{\frac{\pi}{2}}+
 +
-x +\cos(x) \mid_\frac{\pi}{2} ^{\pi}
 +
=
 +
-\frac{\pi}{2}-1 -\pi -1 + \frac{\pi}{2} = -2-\pi
 +
</math>
 +
 +
לכן הפתרון בסך הכל הוא:
 +
 +
<math>\frac{\pi}{2}-1 +2+\pi +\frac{\pi}{2}-1=2\pi</math>

גרסה מ־22:46, 12 בפברואר 2013


שאלה 5

סעיף א

כמו תמיד בחישוב אינטגרל של ערך מוחלט, צריך לפצל לתחום שבו הפונקציה חיובית ותחום שבו היא שלילית.

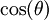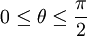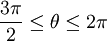במקרה שלנו \cos(\theta) היא חיובית כאשר 0\leq\theta \leq \frac{\pi}{2} וכאשר \frac{3\pi}{2} \leq\theta \leq 2\pi ושלילית כאשר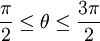 \frac{\pi}{2}\leq\theta \leq \frac{3\pi}{2}

כלומר

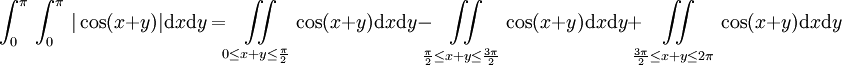
\int _0 ^\pi \, \int_0^\pi \, |\cos(x+y)| \mathrm{d}x\mathrm{d}y = \iint \limits_{0\leq x+y \leq \frac{\pi}{2}} \, \cos(x+y) \mathrm{d}x\mathrm{d}y -\iint \limits_{\frac{\pi}{2}\leq x+y \leq \frac{3\pi}{2}} \, \cos(x+y) \mathrm{d}x\mathrm{d}y +\iint \limits_{\frac{3\pi}{2}\leq x+y \leq 2\pi } \, \cos(x+y) \mathrm{d}x\mathrm{d}y

האינטגרל הראשון הוא:

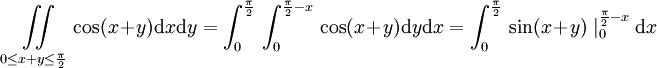
\iint \limits_{0\leq x+y \leq \frac{\pi}{2}} \, \cos(x+y) \mathrm{d}x\mathrm{d}y = \int _0 ^\frac{\pi}{2} \, \int_0^{\frac{\pi}{2}-x} \, \cos(x+y) \mathrm{d}y \mathrm{d}x = \int _0 ^\frac{\pi}{2} \, \sin(x+y) \mid_0^{\frac{\pi}{2}-x} \mathrm{d}x

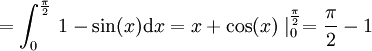
= \int _0 ^\frac{\pi}{2} \, 1 - \sin(x) \mathrm{d}x = x+\cos(x) \mid_0 ^\frac{\pi}{2} = \frac{\pi}{2} - 1

באופן דומה האינטגרל השלישי הוא:

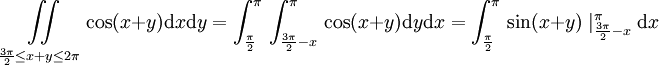
\iint \limits_{\frac{3\pi}{2}\leq x+y \leq 2\pi } \, \cos(x+y) \mathrm{d}x\mathrm{d}y = \int _\frac{\pi}{2} ^{\pi} \, \int_{\frac{3\pi}{2}-x}^{\pi} \, \cos(x+y) \mathrm{d}y\mathrm{d}x = \int _\frac{\pi}{2} ^{\pi} \, \sin(x+y) \mid_{\frac{3\pi}{2}-x}^{\pi} \mathrm{d}x

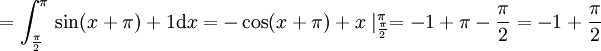
= \int _\frac{\pi}{2} ^{\pi} \, \sin(x+\pi) +1 \mathrm{d}x = -\cos(x+\pi)+x \mid_\frac{\pi}{2} ^{\pi} = -1+\pi - \frac{\pi}{2} = -1+ \frac{\pi}{2}

את האינטגרל השני צריך לפצל

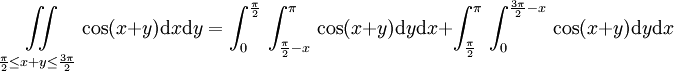
\iint \limits_{\frac{\pi}{2}\leq x+y \leq \frac{3\pi}{2}} \, \cos(x+y) \mathrm{d}x\mathrm{d}y = \int _0 ^{\frac{\pi}{2}} \, \int_{\frac{\pi}{2}-x}^{\pi} \, \cos(x+y) \mathrm{d}y\mathrm{d}x+ \int _\frac{\pi}{2} ^{\pi} \, \int_0^{\frac{3\pi}{2}-x} \, \cos(x+y) \mathrm{d}y\mathrm{d}x

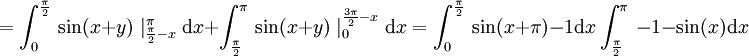
= \int _0 ^{\frac{\pi}{2}} \, \sin(x+y) \mid_{\frac{\pi}{2}-x}^{\pi} \mathrm{d}x+ \int _\frac{\pi}{2} ^{\pi} \, \sin(x+y) \mid_0^{\frac{3\pi}{2}-x} \mathrm{d}x = \int _0 ^{\frac{\pi}{2}} \, \sin(x+\pi) - 1 \mathrm{d}x \int _\frac{\pi}{2} ^{\pi} \, -1 -\sin(x) \mathrm{d}x

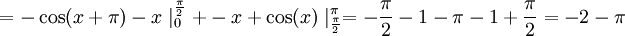
= -\cos(x+\pi) - x \mid_0 ^{\frac{\pi}{2}}+ -x +\cos(x) \mid_\frac{\pi}{2} ^{\pi} = -\frac{\pi}{2}-1 -\pi -1 + \frac{\pi}{2} = -2-\pi

לכן הפתרון בסך הכל הוא:

\frac{\pi}{2}-1 +2+\pi +\frac{\pi}{2}-1=2\pi

מקור: https://math-wiki.com/index.php?title=משתמש:איתמר_שטיין&oldid=32244