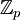הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
שורה 1: שורה 1:
 
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
 
*[[משתמש:איתמר שטיין/הסבר הופכי|הסבר על חישוב הופכי ב <math>\mathbb{Z}_p</math>]]
 +
 +
 +
פתרון הבוחן:
 +
 +
שאלה 1:
 +
 +
נתון כי <math>A = \begin{bmatrix} 1 & a &b \\ 0 & 1 & c \\ 0 & 0 & 1 \end{bmatrix} </math>.
 +
ו <math>B = \begin{bmatrix} 1 & 0 &0 \\ d & 2 & 0 \\ e & f & 3 \end{bmatrix} </math>.
 +
 +
צריך למצוא מטריצות אלמנטריות <math>E_1 , E_2 ,\ldots , E_k</math>. כך ש <math>E_1 \cdot E_2 \cdot \ldots \cdot E_k A =B </math>.
 +
 +
מדרגים את מטריצה <math>A</math> למטריצה <math>B</math>.
 +
 +
<math>\begin{bmatrix} 1 & a &b \\ 0 & 1 & c \\ 0 & 0 & 1 \end{bmatrix} \overset{R_2 = R_2 - cR_3} {\rightarrow} \begin{bmatrix} 1 & a &b \\ 0 &            1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \overset{R_1 = R_1 - bR_3} {\rightarrow} \begin{bmatrix} 1 & a &0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} 
 +
\overset{R_1 = R_1 - aR_2} {\rightarrow}
 +
\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
 +
\overset{R_3 = 3R_3} {\rightarrow}
 +
\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{bmatrix}
 +
\overset{R_3 = R_3 + eR_1} {\rightarrow}
 +
\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & 0 & 3 \end{bmatrix}
 +
</math>
 +
 +
<math>
 +
\overset{R_3 = R_3 + fR_2} {\rightarrow}
 +
\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & f & 3 \end{bmatrix}
 +
\overset{R_2 = 2R_2} {\rightarrow}
 +
\begin{bmatrix} 1 & 0 &0 \\ 0 & 2 & 0 \\ e & f & 3 \end{bmatrix}
 +
\overset{R_2 = R_2 + dR_1} {\rightarrow}
 +
\begin{bmatrix} 1 & 0 &0 \\ d & 2 & 0 \\ e & f & 3 \end{bmatrix}
 +
</math>
 +
 +
לכן מטריצות אלמנטריות מתאימות הן
 +
<math>
 +
E_8=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & -c \\ 0 & 0 & 1 \end{bmatrix}
 +
 +
E_7=\begin{bmatrix} 1 & 0 &-b \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
 +
 +
E_6=\begin{bmatrix} 1 & -a &0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
 +
 +
E_5=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{bmatrix}
 +
 +
E_4=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & 0 & 1 \end{bmatrix}
 +
 +
E_3=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & f & 1 \end{bmatrix}
 +
 +
E_2=\begin{bmatrix} 1 & 0 &0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{bmatrix}
 +
 +
E_1=\begin{bmatrix} 1 & 0 &0 \\ d & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
 +
</math>
 +
 +
ומתקיים <math>E_1 \cdot E_2 \cdot \ldots \cdot E_8 A=B</math>.
 +
 +
(זאת לא התשובה היחידה הנכונה, אבל זאת אחת הפשוטות)

גרסה מ־14:38, 28 באוגוסט 2012


פתרון הבוחן:

שאלה 1:

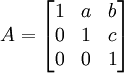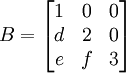נתון כי A = \begin{bmatrix} 1 & a &b \\ 0 & 1 & c \\ 0 & 0 & 1 \end{bmatrix} . ו B = \begin{bmatrix} 1 & 0 &0 \\ d & 2 & 0 \\ e & f & 3 \end{bmatrix} .

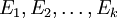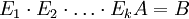צריך למצוא מטריצות אלמנטריות E_1 , E_2 ,\ldots , E_k. כך ש E_1 \cdot E_2 \cdot \ldots \cdot E_k A =B .

מדרגים את מטריצה A למטריצה B.

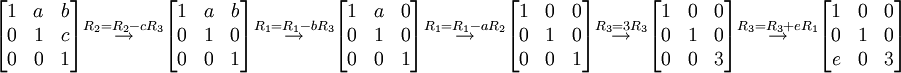
\begin{bmatrix} 1 & a &b \\ 0 & 1 & c \\ 0 & 0 & 1 \end{bmatrix} \overset{R_2 = R_2 - cR_3} {\rightarrow} \begin{bmatrix} 1 & a &b \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \overset{R_1 = R_1 - bR_3} {\rightarrow} \begin{bmatrix} 1 & a &0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \overset{R_1 = R_1 - aR_2} {\rightarrow} \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \overset{R_3 = 3R_3} {\rightarrow} \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{bmatrix} \overset{R_3 = R_3 + eR_1} {\rightarrow} \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & 0 & 3 \end{bmatrix}

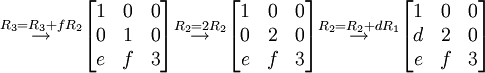
\overset{R_3 = R_3 + fR_2} {\rightarrow} \begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & f & 3 \end{bmatrix} \overset{R_2 = 2R_2} {\rightarrow} \begin{bmatrix} 1 & 0 &0 \\ 0 & 2 & 0 \\ e & f & 3 \end{bmatrix} \overset{R_2 = R_2 + dR_1} {\rightarrow} \begin{bmatrix} 1 & 0 &0 \\ d & 2 & 0 \\ e & f & 3 \end{bmatrix}

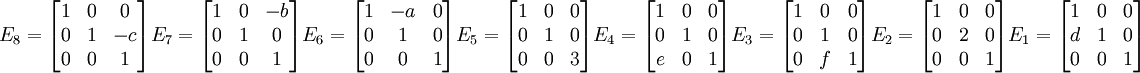
לכן מטריצות אלמנטריות מתאימות הן E_8=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & -c \\ 0 & 0 & 1 \end{bmatrix} E_7=\begin{bmatrix} 1 & 0 &-b \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} E_6=\begin{bmatrix} 1 & -a &0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} E_5=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{bmatrix} E_4=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ e & 0 & 1 \end{bmatrix} E_3=\begin{bmatrix} 1 & 0 &0 \\ 0 & 1 & 0 \\ 0 & f & 1 \end{bmatrix} E_2=\begin{bmatrix} 1 & 0 &0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{bmatrix} E_1=\begin{bmatrix} 1 & 0 &0 \\ d & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}

ומתקיים 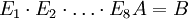E_1 \cdot E_2 \cdot \ldots \cdot E_8 A=B.

(זאת לא התשובה היחידה הנכונה, אבל זאת אחת הפשוטות)

מקור: https://math-wiki.com/index.php?title=משתמש:איתמר_שטיין&oldid=26409