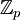שאלה 2
סעיף א
טענת עזר: אם 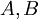 קבוצות חסומות מלעיל אז
קבוצות חסומות מלעיל אז
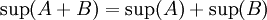
הוכחה: נוכיח שהמספר 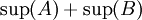 מקיים את התכונות של
מקיים את התכונות של 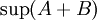
- תכונה א': חסם מלעיל של
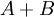 . הוכחה:
. הוכחה:
אם 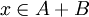 אז ניתן לכתוב
אז ניתן לכתוב 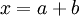 כאשר
כאשר 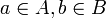 .
.
היות ו 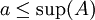 ו
ו 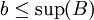 מתקיים
מתקיים
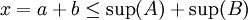
- תכונה ב': החסם המלעיל הכי קטן. הוכחה:
יהי 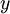 איזשהוא חסם מלעיל של
איזשהוא חסם מלעיל של 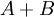
נניח בשלילה ש 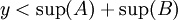
אז נקבל ש 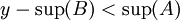
ולכן קיים 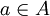 כך ש
כך ש 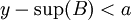
מכאן נקבל 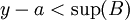
ולכן קיים 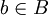 כך ש
כך ש 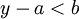
ולכן 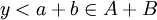
בסתירה לכך ש 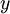 חסם מלעיל של
חסם מלעיל של 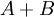
לכן בהכרח מתקיים 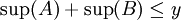
לסיכום: הוכחנו שהמספר 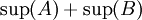 מקיים את שתי התכונות של חסם עליון
מקיים את שתי התכונות של חסם עליון
ולכן 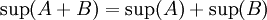 . מש"ל טענת עזר.
. מש"ל טענת עזר.
עכשיו קל להוכיח את הדרוש:
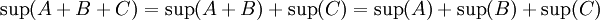
מש"ל.
סעיף ב
הפרכה פשוטה, ניקח 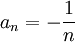 ו
ו 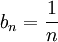
מתקיים שלכל 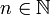
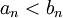 (ולכן בוודאי שזה מקיים כמעט לכל
(ולכן בוודאי שזה מקיים כמעט לכל 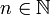 ).
).
אבל
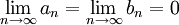
שתי הערות:
א) כמעט לכל  פירושו: לכל
פירושו: לכל  פרט למספר סופי של מקרים.
פרט למספר סופי של מקרים.
אן לחילופין: קיים 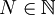 כך שהטענה מתקיימת לכל
כך שהטענה מתקיימת לכל 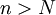 .
.
ב) כמובן שהטענה הבאה נכונה
אם 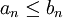 ו
ו
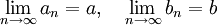
אז
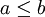 .
.