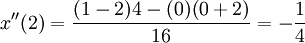משתמש:איתמר שטיין
תוכן עניינים
שאלה 1
סעיף א
עבור נקודות 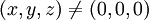 פשוט גוזרים את הפונקציה לפי
פשוט גוזרים את הפונקציה לפי 
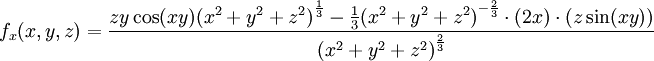
עבור הנקודה 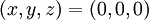 קל לראות ש
קל לראות ש
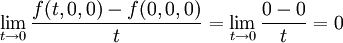
סעיף ב
כמו שראינו בקלות ש 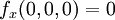 קל לראות שגם
קל לראות שגם 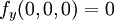 ו
ו 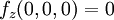 .
.
ראשית נוודא ש  רציפה (לא חייבים, אבל בדר"כ שווה לבדוק. כי אם היא לא רציפה אז ברור שהיא לא דיפרנציאבילית).
רציפה (לא חייבים, אבל בדר"כ שווה לבדוק. כי אם היא לא רציפה אז ברור שהיא לא דיפרנציאבילית).
נשים לב ש
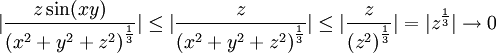
ולכן  רציפה.
רציפה.
נבדוק דיפרנציאביליות
צריך לבדוק אם 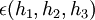 המוגדרת לפי:
המוגדרת לפי:
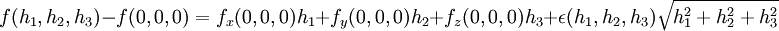
מתכנסת ל 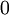 בנקודה
בנקודה 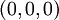 .
.
במקרה שלנו צריך לבדוק את:
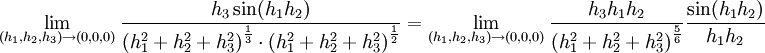
היות ו
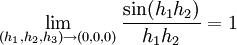
נותר לבדוק את
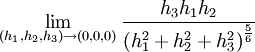
נשים לב ש
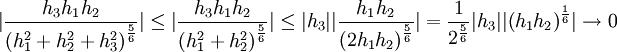
דרך אחרת (שימושית כאשר יש במכנה דברים בסגנון 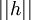 ):
):
עוברים לקוארדינטות כדוריות
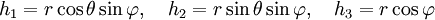
ואז צריך לחשב גבול
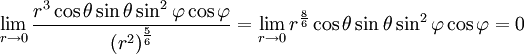
ולכן  דיפרנציאבילית ב
דיפרנציאבילית ב 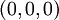 .
.
שאלה 3
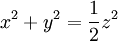
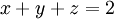
הנגזרות החלקיות של הפונקציות
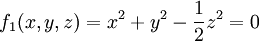
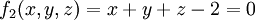
קיימות עד איזה סדר שרוצים.
כמו כן, הנקודה 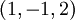 מקיימת את מערכת המשוואות.
מקיימת את מערכת המשוואות.
נבדוק את התנאי של משפט הפונקציה הסתומה
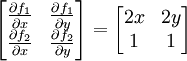
בנקודה 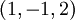 נקבל את המטריצה
נקבל את המטריצה
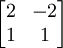
שהיא מטריצה הפיכה.
לכן לפי משפט הפונקציה הסתומה, אכן מוגדרות פונקציות של
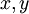 לפי
לפי 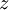
לפי משפט הפונקציה הסתומה, קיימת סביבה של הנקודה
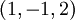 שבה מתקיים:
שבה מתקיים:
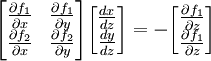
כלומר במקרה שלנו:
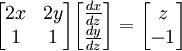
אם פותרים את המשוואות
רואים ש
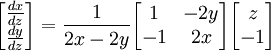
כלומר:
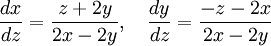
מכאן, על ידי הצבה של 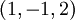 קל לראות שבנקודה
קל לראות שבנקודה 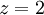 מתקיים
מתקיים
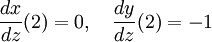
כמו כן נחשב את 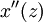 בסביבה של
בסביבה של 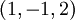 על ידי גזירה רגילה לפי
על ידי גזירה רגילה לפי 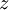 (אבל נשים לב ש
(אבל נשים לב ש 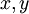 הם פונקציות של
הם פונקציות של 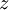 ):
):
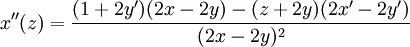
נציב 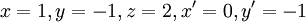 ונקבל:
ונקבל: