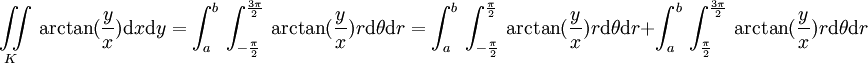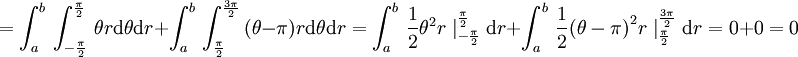משתמש:איתמר שטיין
מתוך Math-Wiki
שאלה 5
סעיף א
דרך א' לפתרון:
היות ו  היא פונקציה אי זוגית לפי
היא פונקציה אי זוגית לפי 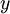 (או
(או  ) והתחום שלנו סימטרי ביחס ל
) והתחום שלנו סימטרי ביחס ל 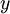 (או
(או  ) אז האינטגרל הוא
) אז האינטגרל הוא 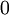 .
.
דרך ב', חישוב:
זה די ברור שצריך להשתמש בקוארדינטות פולריות.
אם מחליפים
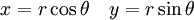
אז נקבל שהתחום החדש הוא 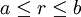 ו
ו 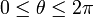
הבעיה היחידה היא זה לא נכון להגיד ש 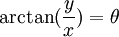 .
.
זה נכון רק כש 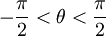
בתחום 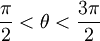 מתקיים דווקא
מתקיים דווקא 
ולכן נעדיף ש 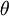 יהיה בתחום
יהיה בתחום ![[-\frac{\pi}{2},\frac{3\pi}{2}]](/images/math/1/6/8/1686615fb75a05db936a11ad0e86f75c.png) ולא
ולא ![[0,2\pi]](/images/math/5/8/c/58c9a5de0cb1a343ae0acd1fb191eea1.png)