הבדלים בין גרסאות בדף "משתמש:איתמר שטיין/הסבר הופכי"
מתוך Math-Wiki
איתמר שטיין (שיחה | תרומות) (יצירת דף עם התוכן "כאשר אנו מבצעים חישובים בשדה <math>\mathbb{Z}_p</math> (נזכור ש <math>p</math> חייב להיות ראשוני), אנו נדרשים ...") |
איתמר שטיין (שיחה | תרומות) |
||
| שורה 9: | שורה 9: | ||
שיטה זו טובה לשדות קטנים, אבל מה עושים אם רוצים למצוא הופכי ב <math>\mathbb{Z}_{101}</math>? בשיטה הזאת נצטרך לנסות 99 אפשרויות. | שיטה זו טובה לשדות קטנים, אבל מה עושים אם רוצים למצוא הופכי ב <math>\mathbb{Z}_{101}</math>? בשיטה הזאת נצטרך לנסות 99 אפשרויות. | ||
| + | |||
| + | כדי להסביר איך מוצאים הופכי ב <math>\mathbb{Z}_p</math> נצטרך להביא כמה הקדמות מתורת המספרים. | ||
| + | |||
| + | == כמה מושגים בתורת המספרים == | ||
| + | הגדרה: יהיו <math>a,b\in \mathbb{Z}</math> אומרים ש <math>a</math> מחלק את <math>b</math> (ומסמנים <math>a|b</math>) | ||
| + | אם קיים <math>c\in \mathbb{Z}</math> כך ש <math>ac=b</math>. | ||
| + | |||
| + | |||
| + | הגדרה: יהיו <math>a,b\in \mathbb{Z}</math> המחלק המשותף המירבי של <math>a,b</math> (מסומן <math>gcd(a,b)</math>) הוא המספר הגדול ביותר שמחלק גם את <math>a</math> וגם את <math>b</math>. | ||
| + | |||
| + | כלומר <math>gcd(a,b)=max\{g\in \mathbb{Z}\mid g|a\quad g|b\}</math> | ||
| + | |||
| + | ההגדרה הזאת בעייתית כאשר <math>a=b=0</math> במצב זה אומרים ש <math>gcd(0,0)=0</math>. | ||
גרסה מ־10:35, 11 ביולי 2012
כאשר אנו מבצעים חישובים בשדה 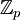 (נזכור ש
(נזכור ש 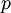 חייב להיות ראשוני), אנו נדרשים לפעמים לחשב הופכי לאיבר מסוים בשדה.
חייב להיות ראשוני), אנו נדרשים לפעמים לחשב הופכי לאיבר מסוים בשדה.
שיטה אחת לבצע זאת היא ע"י ניחוש,
אם 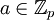 אז יש
אז יש 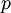 איברים שיכולים להיות הופכי:
איברים שיכולים להיות הופכי: 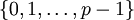
(למעשה יש פחות, כי 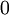 לעולם לא יהיה הופכי ו
לעולם לא יהיה הופכי ו 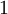 הופכי רק ב
הופכי רק ב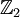 )
)
אפשר פשוט לנסות את כל האפשרויות עד שמוצאים הופכי.
שיטה זו טובה לשדות קטנים, אבל מה עושים אם רוצים למצוא הופכי ב 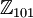 ? בשיטה הזאת נצטרך לנסות 99 אפשרויות.
? בשיטה הזאת נצטרך לנסות 99 אפשרויות.
כדי להסביר איך מוצאים הופכי ב 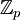 נצטרך להביא כמה הקדמות מתורת המספרים.
נצטרך להביא כמה הקדמות מתורת המספרים.
כמה מושגים בתורת המספרים
הגדרה: יהיו 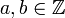 אומרים ש
אומרים ש 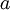 מחלק את
מחלק את 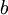 (ומסמנים
(ומסמנים 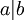 )
אם קיים
)
אם קיים 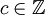 כך ש
כך ש 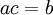 .
.
הגדרה: יהיו 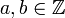 המחלק המשותף המירבי של
המחלק המשותף המירבי של 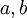 (מסומן
(מסומן 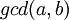 ) הוא המספר הגדול ביותר שמחלק גם את
) הוא המספר הגדול ביותר שמחלק גם את 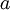 וגם את
וגם את 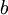 .
.
כלומר 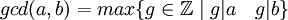
ההגדרה הזאת בעייתית כאשר 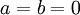 במצב זה אומרים ש
במצב זה אומרים ש 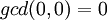 .
.