הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' עברית, תשס"ב, מועד ב, שאלה 3"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
מ
 
שורה 1: שורה 1:
 
[[תחרות חנוכה לינארית 2 תשעב|חזרה]]
 
[[תחרות חנוכה לינארית 2 תשעב|חזרה]]
  
−
ידוע שמטריצות דומות <=> צורת ז'ורדן שלהן זהה. נראה של A,B יש צורת ז'ורדן שונה, ולכן הן אינן דומות:  
+
ידוע שמטריצות הן דומות אם ורק אם יש להן אותה צורת ז'ורדן (עד כדי סדר הבלוקים). שתי המטריצות בשאלה כבר נתונות כסכום של בלוקי ז'ורדן:  
  
−
 
+
<math>
−
נז'רדן את <math>A</math>:
+
A=\begin{pmatrix}
−
 
+
−
<math>A=\begin{pmatrix}
+
 
0 & 1 &0  & 0\\  
 
0 & 1 &0  & 0\\  
 
  0& 0 &0  &0 \\  
 
  0& 0 &0  &0 \\  
 
0 & 0 &  0&1 \\  
 
0 & 0 &  0&1 \\  
 
  0& 0 &0  &0 \\
 
  0& 0 &0  &0 \\
−
\end{pmatrix}</math>
+
\end{pmatrix} = \left(
−
 
+
\begin{array}{cc}
−
 
+
\begin{array}{cc} 0 & 1 \\ 0 & 0\end{array} &  \begin{array}{cc} 0 & 0 \\ 0 & 0\end{array} \\
−
נמצא פ"א:
+
\\
−
 
+
\begin{array}{cc} 0 & 0 \\ 0 & 0\end{array} &  \begin{array}{cc} 0 & 1 \\ 0 & 0\end{array}
−
<math>p_A(x)=|xI-A|=\begin{vmatrix}
+
\end{array}\right) = \begin{pmatrix} J_2(0) & 0 \\ 0 & J_2(0)\end{pmatrix} = J_2(0) \oplus J_2(0),
−
x & -1 &0 & 0\\
+
</math>
−
0& x &0 &0 \\
+
−
0 & 0 &  x&-1 \\  
+
−
0& 0 &0  &x \\
+
−
\end{vmatrix}=x^4</math>
+
−
 
+
−
שכן דטר' של מטר' משולשית שווה למכפלת איברי האלכסון הראשי.
+
−
 
+
−
כעת, <math>A^2=0</math> ולכן <math>A</math> נילפוטנטית מסדר 2, והפ"מ שלה הוא <math>m_A(x)=x^2</math>.
+
−
 
+
−
דרגת המטריצה היא 2 (מס' השורות הלא אפסיות, אחרי שמחליפים שורות והיא הופכת למטריצת מדרגות), והיא נילפוטנטית, ולכן <math>n-rank(A)=4-2=2</math> הוא מס' הבלוקים בצורת ז'ורדן. לכן צורת ז'ורדן של <math>A</math> היא
+
−
 
+
−
 
+
−
<math>\begin{pmatrix}
+
−
J_2 & \\  
+
−
& J_2
+
−
\end{pmatrix}=\begin{pmatrix}
+
−
0 &1 &0  &0 \\  
+
−
0& 0 & 0 &0 \\  
+
−
0 & 0 &  0 &1\\  
+
−
0 & 0 & 0 &0
+
−
\end{pmatrix}</math>
+
−
.
+
−
 
+
−
 
+
−
כעת נז'רדן את <math>B</math>:
+
−
 
+
  
 +
ואילו
 
<math>B=\begin{pmatrix}
 
<math>B=\begin{pmatrix}
 
0 & 1 &0  & 0\\  
 
0 & 1 &0  & 0\\  
שורה 50: שורה 23:
 
0 & 0 &  0&0 \\  
 
0 & 0 &  0&0 \\  
 
  0& 0 &0  &0 \\
 
  0& 0 &0  &0 \\
−
\end{pmatrix}</math>
+
\end{pmatrix}
−
 
+
= \left(
−
נמצא פ"א:
+
\begin{array}{cc}
−
<math>p_B(x)=|xI-B|=\begin{vmatrix}
+
\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array} &  \begin{array}{c} 0 \\  0 \\ 0\end{array} \\
−
x & -1 &0  & 0\\
+
\\
−
0& x &-1  &0 \\
+
\begin{array}{ccc} 0 & 0 & 0 \end{array} &  0
−
0 & 0 &  x&0 \\
+
\end{array}\right) = \begin{pmatrix} J_3(0) & 0 \\ 0 & J_1(0)\end{pmatrix} = J_3(0) \oplus J_1(0),
−
0& 0 &0  &x \\
+
−
\end{vmatrix}=x^4</math>
+
−
 
+
−
כעת נמצא את אינדקס הנילפוטנטיות של B, ובכך גם את הפ"מ שלה:
+
−
 
+
−
 
+
−
<math>B^2=\begin{pmatrix}
+
−
0 & 1 &0  & 0\\  
+
−
0& 0 &1 &0 \\  
+
−
0 & 0 &  0&0 \\
+
−
0& 0 &0  &0 \\
+
−
\end{pmatrix}^2=\begin{pmatrix}
+
−
0 & 0 &1  & 0\\  
+
−
  0& 0 &0  &0 \\  
+
−
0 & 0 &  0&0 \\
+
−
0& 0 &0  &0 \\
+
−
\end{pmatrix}\neq 0_{4 \times 4}</math>
+
−
 
+
−
ואילו <math>B^3=\begin{pmatrix}
+
−
0 & 1 &0 & 0\\
+
−
0& 0 &1  &0 \\
+
−
0 & 0 &  0&0 \\
+
−
0& 0 &0  &0 \\
+
−
\end{pmatrix}^3=\begin{pmatrix}
+
−
0 & 1 &0 & 0\\
+
−
0& 0 &1  &0 \\
+
−
0 & 0 &  0&0 \\
+
−
0& 0 &0  &0 \\
+
−
\end{pmatrix}\cdot \begin{pmatrix}
+
−
0 & 0 &1  & 0\\  
+
−
0& 0 &0  &0 \\
+
−
0 & 0 &  0&0 \\
+
−
0& 0 &0  &0 \\
+
−
\end{pmatrix}=0_{4 \times 4}
+
 
</math>
 
</math>
−
 
−
ולכן B נילפ' מאינדקס 3, והפ"מ שלה הוא <math>m_B(x)=x^3</math>.
 
−
 
−
לכן בצורת ז'ורדן של <math>B</math> יופיע בלוק ז'ורדן נילפוטנטי מסדר 3, והמטריצה היא מסדר 4; לכן צורת ז'ורדן של A היא <math>\begin{pmatrix}
 
−
J_3 & \\
 
−
& J_1
 
−
\end{pmatrix}</math>.
 
  
 
קיבלנו שצורות ז'ורדן של שתי המטריצות הנתונות שונות, ולכן הן '''אינן דומות.'''
 
קיבלנו שצורות ז'ורדן של שתי המטריצות הנתונות שונות, ולכן הן '''אינן דומות.'''
  
−
מש"ל סעיף א'.
+
נימוק אחר: חישוב ישיר מראה ש-<math>\ A^2 = 0</math> בעוד ש-<math>\ B^2 \neq 0</math>. לכן הן אינן יכולות להיות דומות.
−
 
+
  
 
----
 
----

גרסה אחרונה מ־23:46, 8 בינואר 2012

חזרה

ידוע שמטריצות הן דומות אם ורק אם יש להן אותה צורת ז'ורדן (עד כדי סדר הבלוקים). שתי המטריצות בשאלה כבר נתונות כסכום של בלוקי ז'ורדן:

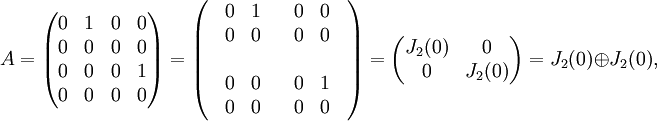
A=\begin{pmatrix} 0 & 1 &0 & 0\\ 0& 0 &0 &0 \\ 0 & 0 & 0&1 \\ 0& 0 &0 &0 \\ \end{pmatrix} = \left( \begin{array}{cc} \begin{array}{cc} 0 & 1 \\ 0 & 0\end{array} & \begin{array}{cc} 0 & 0 \\ 0 & 0\end{array} \\ \\ \begin{array}{cc} 0 & 0 \\ 0 & 0\end{array} & \begin{array}{cc} 0 & 1 \\ 0 & 0\end{array} \end{array}\right) = \begin{pmatrix} J_2(0) & 0 \\ 0 & J_2(0)\end{pmatrix} = J_2(0) \oplus J_2(0),

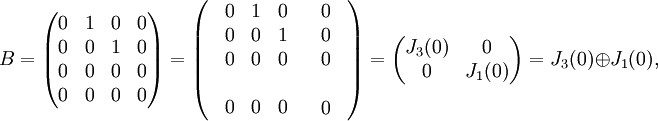
ואילו B=\begin{pmatrix} 0 & 1 &0 & 0\\ 0& 0 &1 &0 \\ 0 & 0 & 0&0 \\ 0& 0 &0 &0 \\ \end{pmatrix} = \left( \begin{array}{cc} \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array} & \begin{array}{c} 0 \\ 0 \\ 0\end{array} \\ \\ \begin{array}{ccc} 0 & 0 & 0 \end{array} & 0 \end{array}\right) = \begin{pmatrix} J_3(0) & 0 \\ 0 & J_1(0)\end{pmatrix} = J_3(0) \oplus J_1(0),

קיבלנו שצורות ז'ורדן של שתי המטריצות הנתונות שונות, ולכן הן אינן דומות.

נימוק אחר: חישוב ישיר מראה ש-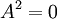\ A^2 = 0 בעוד ש-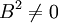\ B^2 \neq 0. לכן הן אינן יכולות להיות דומות.

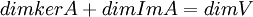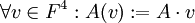סעיף ב': ידוע מלינארית 1 שמתקיים dimkerA+dimImA=dimV, כאשר V המ"ו שעליו פועלת הטרנספורמציה A (\forall v \in F^4: A(v):=A\cdot v)

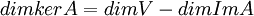ולכן dimkerA=dimV-dimImA.

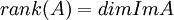ידוע גם rank(A)=dimImA=מספר השורות הלא אפסיות בצורה המדורגת של A, כלומר 2.

כמו כן 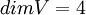dimV=4 שכן מסתכלים על A כעל הע"ל מהמרחב 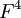F^4 לעצמו.

לכן בסה"כ 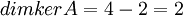dimkerA=4-2=2.


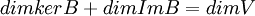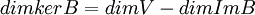באופן דומה עבור B, מתקיים dimkerB+dimImB=dimV, ולכן dimkerB=dimV-dimImB.

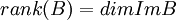ידוע גם rank(B)=dimImB=מספר השורות הלא אפסיות בצורה המדורגת של B, כלומר 2.

כמו כן 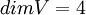dimV=4 שכן מסתכלים על B כעל הע"ל מהמרחב 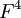F^4 לעצמו.

לכן בסה"כ 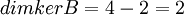dimkerB=4-2=2.

(ידוע ש-A היא המטריצה המייצגת של הטרנספורמציה המוגדרת בעזרתה וכו' - כל זה מלינארית 1, אין צורך לפרט)


לסיכום, קיבלנו 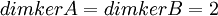dimkerA=dimkerB=2. מש"ל!

מקור: https://math-wiki.com/index.php?title=פתרון_לינארית_2,_אונ%27_עברית,_תשס%22ב,_מועד_ב,_שאלה_3&oldid=18225