פתרונות לקורס לינארית 2 לתיכוניסטים תש"ע - תרגיל 2
מתוך Math-Wiki
תרגיל 2
תרגיל 2.14
הראנו בתרגיל 1.10 ש 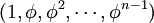 הוא וקטור עצמי עבור
הוא וקטור עצמי עבור 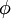 שורש יחידה מסדר
שורש יחידה מסדר  . נרצה להוכיח שעבור
. נרצה להוכיח שעבור  שורשי היחידה השונים מתקבלים
שורשי היחידה השונים מתקבלים  וקטורים עצמיים שונים ובת"ל. נמקם את הוקטורים האלה בשורה ונקבל מטריצת ונדרמונדה. הדטרמיננטה של מטריצה זו היא
וקטורים עצמיים שונים ובת"ל. נמקם את הוקטורים האלה בשורה ונקבל מטריצת ונדרמונדה. הדטרמיננטה של מטריצה זו היא 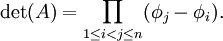 . מכיוון ששורשי היחידה שונים זה מזה,
. מכיוון ששורשי היחידה שונים זה מזה, 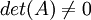 כלומר הוקטורים העצמיים בת"ל. ולכן הם פורסים מרחב ממימד
כלומר הוקטורים העצמיים בת"ל. ולכן הם פורסים מרחב ממימד  ולכן המטריצה לכסינה.
ולכן המטריצה לכסינה.
חישוב הדטרמיננטה של מטריצת ונדרמונדה
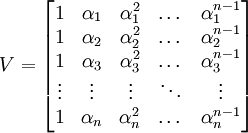
- לפי האלגוריתם בספר, נחסיר מכל עמודה את העמודה הקודמת כפול
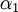 לקבל:
לקבל:
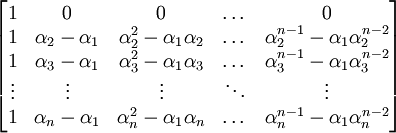
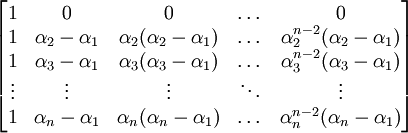
- נחשב את הדטרמיננטה לפי השורה הראשונה לקבל
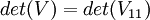 .
. - ב
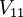 נחלק כל שורה
נחלק כל שורה 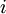 ב
ב 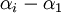 ונמשיך באינדוקציה.
ונמשיך באינדוקציה.