פתרונות לקורס לינארית 2 לתיכוניסטים תש"ע - תרגיל 5
מתוך Math-Wiki
תוכן עניינים
תרגיל 5
שאלה 1.4
א. זכרו שהמכפלה הפנימית הסטנדרטית מעל הממשיים היא 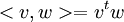 ובמקרה זה
ובמקרה זה 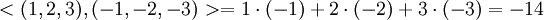
ב.
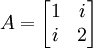 ,
,
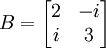
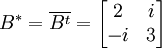
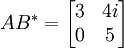
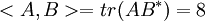
ג.
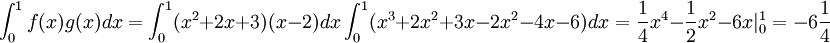
שאלה 1.5
מכפלה פנימית חייבת לקיים את התכונה 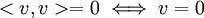 . ניקח לדוגמא
. ניקח לדוגמא 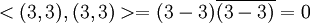 אבל כמובן
אבל כמובן 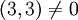
שאלה 1.9
ב. ![[A]_{ij}=<v_i,v_j>=\overline{<v_j,v_i>}=[\overline{A^t}]_{ij}=[A^*]_{ij}](/images/math/d/2/e/d2e1bdbe9525ae0a713f71127eb0d50e.png) .
.
![[A]_{ii}=<v_i,v_i>\geq 0](/images/math/7/d/8/7d8ae2452c703c4290893029b6026524.png) (אי שליליות)
(אי שליליות)
ג.
ניקח 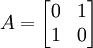 . ויוצא ש
. ויוצא ש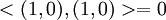 אבל
אבל 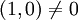 בסתירה לתכונות המכפלה.
בסתירה לתכונות המכפלה.
שאלה 4.11
א. נניח 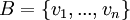 בא"נ. יהיה וקטור
בא"נ. יהיה וקטור 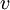 אזי יש הצגה
אזי יש הצגה 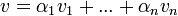 .
.
לכן 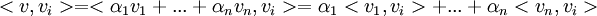 .
.
אבל  בא"נ ולכן
בא"נ ולכן 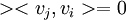 עבור
עבור 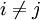 וכמו כן
וכמו כן 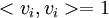 ולכן בסיכום:
ולכן בסיכום:
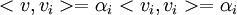
שאלה 1/2 4.12
נניח 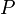 אוניטרית, לכן
אוניטרית, לכן 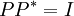 . נזכר ש
. נזכר ש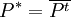 ולכן
ולכן
![[PP^*]_{ij}=R_i(P)C_j(P^*)=R_i(P)\overline{R_j(P)}^t=<R_i(P),R_j(P)>](/images/math/c/d/3/cd31a8edfafc0e79f86a8cb2cd2c508d.png)
נובע מזה ששורות 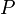 מהוות בא"נ אם"ם
מהוות בא"נ אם"ם 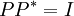 .
.
כעת, 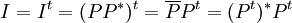 ולכן
ולכן 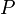 אוניטרית אם"ם
אוניטרית אם"ם 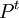 אוניטרית.
אוניטרית.
ולפי מה שראינו 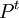 אוניטרית אם"ם שורותיה הם בא"נ, אבל אלה בדיוק עמודות
אוניטרית אם"ם שורותיה הם בא"נ, אבל אלה בדיוק עמודות 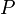
שאלה 4.22 ב'
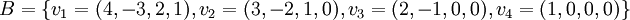
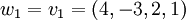
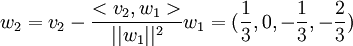
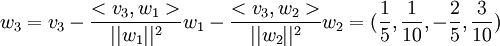
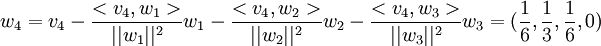
ועכשיו נותר לנרמל את הוקטורים על מנת לקבל בסיס אורתונורמלי: