שיחה:88-132 סמסטר א' תשעא/ ארכיון 15
תוכן עניינים
- 1 שאלה לגבי המבחן
- 2 שאלה על פתרון לתרגיל
- 3 שאלה קודמת (טור)
- 4 שאלה 1 מועד א 2007 של זלצמן
- 5 התכנסות
- 6 כלל לופיטל
- 7 מבחן ההשוואה ה2
- 8 שאלה לגבי גבולות
- 9 משפט רימן
- 10 עזרה בפתרון שאלה
- 11 הוכחת אינדוקציה
- 12 מבחן באינפי
- 13 תרגילים
- 14 פתרון מבחנים
- 15 פונקציה הפוכה
- 16 עזרה בקביעת התכנסות טור
- 17 שאלה ממבחן
- 18 נגזרת arctan, arcsin, arccos
- 19 רציפות במ"ש
- 20 שלבים לקביעת התכנסות טור
- 21 פונקציה מעריכית
- 22 log
- 23 שאלה על סדרות
- 24 שאלה ממבחן
- 25 תקלה באתר
- 26 מבחן
- 27 מיבחן המנה
- 28 זיהוי וסיווג נקודות אי רציפות של הפונקציה
- 29 מה מידת הדיוק שנדרשת בשאלות של גזירת פונקציות?
- 30 אי רציפות
- 31 מועד ב' של שנה שעברה
שאלה לגבי המבחן
מישהו יכול בבקשה לפרט אילו שאלות עלולות להופיע במבחן באינפי 1 ביום שני?? יופיעו שאלות חישוביות??
שאלה על פתרון לתרגיל
http://math-wiki.com/images/b/b5/10Infi1Targil11Sol.pdf פה, תרגיל 11, בשאלה 1, כתבת:
"כפי שראינו בכיתה, ניתן להשלים את f לפונקציה רציפה בקטע הסגור a M [ , 1] ולכן היא רציפה שם במ"ש". תוכל להרחיב בנושא? ניתן להוכיח את התרגיל בלי לעשות טריקים כאלה של השלמה?
וגם, בקטע עם דלתא, כתבת "ניתן לבחור 1>ל>0". למה? איך יודעים מהו דלתא? וגם למה צריך את זה? אפשר להוכיח את הקטע הזה בדרך אחרת ע"י השימוש בזה שהגבול בa מימין קיים, ולהראות ש-f רציפה במ"ש ב ![(a,M]](/images/math/4/0/a/40a2ba2d0a20ad56b298c7e3bd10c4ad.png) ?
?
- יש לה אי רציפות סליקה בa ולכן ההשלמה הזו זה סילוק אי הרציפות על ידי הגדרת הערך של הפונקציה בa להיות הגבול שם מימין. לגבי הדלתא, אם משהו נכון עבור דלתא גדול מאחד, הוא בוודאי נכון לכל דלתא קטן מאחד. אנחנו עושים את זה על מנת שלא יצאו לנו שתי נקודות כך שאחת בקטע האינסופי ואחת בקטע הסופי (לכן יש חפיפה בינהם). --ארז שיינר 19:24, 24 בינואר 2011 (IST)
- כמה שאלות: -למה לפונקציה אי רציפות סליקה בa? למה אם משהו נכון עבור דלתא גדול מאחד, הוא נכון גם לדלתא קטן מיוחד (כפי שאני רואה את זה- אם x<d=2 אז לא בהכרח x<1)? -בשביל מה הקטע החופף? בשביל שיהיה "אותו דלתא" גם אם x שייך לקטע האינסופי וגם לסופי? אבל בקטע האינסופי אין בכלל דלתא! תודה.
- כי יש לה גבול סופי בa זו ההגדרה של אי רציפות סליקה. אמנם זה חד צדדי, אבל זה מספיק כי זה קצה הקטע (פונקציה רציפה ב[a,b] אם היא רציפה בקטע הפתוח וקיימים לה הגבולות החד צדיים בקצות הקטע ושווים לערך הפונקציה שם). הכוונה היא שאם קיים דלתא (נניח 2) כך שלכל איקס שקרוב לאיקס אפס עד כדי דלתא משהו קורה, בפרט המשהו הזה קורה לכל איקס שקרוב לאיקס אפס עד כדי דלתא קטן יותר (נגיד אחד) כי זה אפילו קרוב יותר. יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם. --ארז שיינר 20:09, 24 בינואר 2011 (IST)
- 2 דברים- לא הבנתי את הקטע של עד כדי דלתא, בד"כ (בפרט בהוכחה של רציפות במ"ש צריך להוכיח שאם משהו (ברציפות במ"ש |x1-x2|<דלתא) אז קורה משהו (..קטן מאפסילון) ופה אם משהו נכון לדלתא כלשהו הוא לא בהכרח נכון לדלתא קטן יותר (אז לא הבנתי נכון את הכוונה). דבר שני, לגבי יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם"- אבל בפועל כן יכולים להיות 2 איקסים שאחד בקטע ובשני לא, אז אם ההוכחה לא תקפה לגביהם, היא לא נכונה עבורם- ואז לא נכונה תמיד?
- בגלל שדלתא קטן מאחד, לא יכולים להיות שני איקסים במרחק אחד שלא מוכלים שניהם באחד הקטעים. לגבי הדלתא: אם לכל
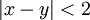 מתקיים
מתקיים 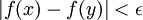 בוודאי נכון לומר שלכל
בוודאי נכון לומר שלכל 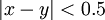 מתקיים
מתקיים 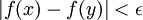 . --ארז שיינר 21:32, 24 בינואר 2011 (IST)
. --ארז שיינר 21:32, 24 בינואר 2011 (IST)
- בגלל שדלתא קטן מאחד, לא יכולים להיות שני איקסים במרחק אחד שלא מוכלים שניהם באחד הקטעים. לגבי הדלתא: אם לכל
- 2 דברים- לא הבנתי את הקטע של עד כדי דלתא, בד"כ (בפרט בהוכחה של רציפות במ"ש צריך להוכיח שאם משהו (ברציפות במ"ש |x1-x2|<דלתא) אז קורה משהו (..קטן מאפסילון) ופה אם משהו נכון לדלתא כלשהו הוא לא בהכרח נכון לדלתא קטן יותר (אז לא הבנתי נכון את הכוונה). דבר שני, לגבי יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם"- אבל בפועל כן יכולים להיות 2 איקסים שאחד בקטע ובשני לא, אז אם ההוכחה לא תקפה לגביהם, היא לא נכונה עבורם- ואז לא נכונה תמיד?
- כי יש לה גבול סופי בa זו ההגדרה של אי רציפות סליקה. אמנם זה חד צדדי, אבל זה מספיק כי זה קצה הקטע (פונקציה רציפה ב[a,b] אם היא רציפה בקטע הפתוח וקיימים לה הגבולות החד צדיים בקצות הקטע ושווים לערך הפונקציה שם). הכוונה היא שאם קיים דלתא (נניח 2) כך שלכל איקס שקרוב לאיקס אפס עד כדי דלתא משהו קורה, בפרט המשהו הזה קורה לכל איקס שקרוב לאיקס אפס עד כדי דלתא קטן יותר (נגיד אחד) כי זה אפילו קרוב יותר. יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם. --ארז שיינר 20:09, 24 בינואר 2011 (IST)
שאלה קודמת (טור)
עדיין לא הבנתי פתרון לשאלה ששאלתי וכעת שייכת לארכיון - [[1]] תודה!
- אני לא יודע מה הקשר לקטן או גדול זה עניין של גבול. אם
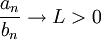 אזי הטורים a_n וb_n מתכנסים יחדיו (חברים). --ארז שיינר 20:41, 24 בינואר 2011 (IST)
אזי הטורים a_n וb_n מתכנסים יחדיו (חברים). --ארז שיינר 20:41, 24 בינואר 2011 (IST)
- וואו, לא היה זכור לי משפט כזה, מזל ששאלתי. תודה
- אני לא יודע אם זה בדיוק משפט. פשוט מבחן ההשוואה השני נובע מזה בקלות - קיים אפסילון כך ש
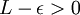 והחל משלב מסויים מתקיים
והחל משלב מסויים מתקיים 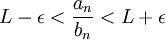 . --ארז שיינר 21:29, 24 בינואר 2011 (IST)
. --ארז שיינר 21:29, 24 בינואר 2011 (IST)
- אני לא יודע אם זה בדיוק משפט. פשוט מבחן ההשוואה השני נובע מזה בקלות - קיים אפסילון כך ש
- וואו, לא היה זכור לי משפט כזה, מזל ששאלתי. תודה
שאלה 1 מועד א 2007 של זלצמן
תהי 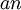 סדרה כך ש
סדרה כך ש 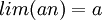 ו
ו 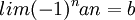 הוכח:
הוכח: 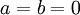
אשמח אם מישהו יגיד לי אם פתרתי נכון, כי אני לא כלכך בטוח בכך.
פתרון:
נניח ש 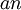 סדרה חיובית (בהמשך נוכיח לגבי סדרה שלילית וסדרה מעורבת או שאני אגיד שבאופן דומה אפשר להוכיח..)
סדרה חיובית (בהמשך נוכיח לגבי סדרה שלילית וסדרה מעורבת או שאני אגיד שבאופן דומה אפשר להוכיח..)
ידוע שהסדרה 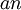 שואפת לגבול a ולכן נכתוב לפי הגדרת הגבול
שואפת לגבול a ולכן נכתוב לפי הגדרת הגבול
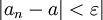
לכן גם
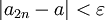 בנוסף,
בנוסף,
ניתן לתאר את הסדרה 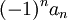 בצורה הבאה :
בצורה הבאה :
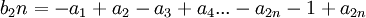 כלומר:
כלומר:
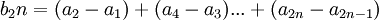
כלומר:
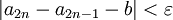 לפי הנתון.
לפי הנתון.
היות ו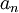 חיובית, נוכל לרשום(כמסקנה מהמשוואות עד עתה) את הדבר הבא
חיובית, נוכל לרשום(כמסקנה מהמשוואות עד עתה) את הדבר הבא
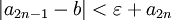
ולכן :
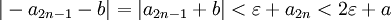
ולכן
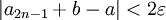
הגבול של 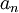 של
של 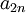 ושל
ושל 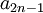 הוא אותו גבול
הוא אותו גבול
ולכן 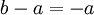
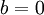
הצלחתי להגיע עד לפה. אשמח לדעת אם הפתרון שי עד לפה בסדר, ואם הוא טוב אז איך ממשיכים
פתרון נוסף
(לא מתרגל/ת): נראה לי שזה בסדר מה שעשית, אבל אני לא כל כך רואה איך אפשר להכליל את מה שעשית לסדרות אחרות, אשמח גם אני להסבר.
בכל אופן אני פתרתי את זה בדרך אחרת, אשמח למשוב:
הסדרה 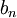 היא מהצורה
היא מהצורה 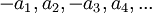 . ידוע שהיא מתכנסת לגבול
. ידוע שהיא מתכנסת לגבול 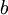 ולכן כל תת סדרה שלה תתכנס לגבול זה.
אם נתבונן בתת הסדרה של האיברים במקומות הזוגיים נקבל שהיא שואפת ל-
ולכן כל תת סדרה שלה תתכנס לגבול זה.
אם נתבונן בתת הסדרה של האיברים במקומות הזוגיים נקבל שהיא שואפת ל-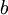 אבל באותו אופן גם ל-
אבל באותו אופן גם ל-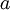 (עפ"י נתון התכנסות הסדרה
(עפ"י נתון התכנסות הסדרה 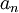 ) ולכן
) ולכן 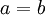 .
אם נתבונן בתת הסדרה של האיברים במקומות האי זוגיים נקבל שהיא שואפת ל-
.
אם נתבונן בתת הסדרה של האיברים במקומות האי זוגיים נקבל שהיא שואפת ל-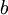 וגם ל
וגם ל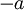 ולכן
ולכן 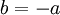 .
נפתור מערכת משוואות ונקבל ש-
.
נפתור מערכת משוואות ונקבל ש-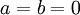 .
.
איך הפתרון הזה? תודה מראש, גל א.
(לא מתרגל/ת): הוספתי לאחר התנגשות עריכה - לא יודע לגבי ההוכחה הזו (אני יודע להוכיח את הטענות האלה, אבל ההוכחות לא מסתדרות עם ההסברים שלך. אולי התבלבת עם הפלוסים והמינוסים?), אבל ראה/י שאלה 7 בתרגיל 3.
התכנסות
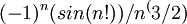 האם בגלל שהטור שואף ל0 זה מספיק כדי להגיד שתנאי לייבניץ מתקיים והוא מתכנס בתנאי?
האם בגלל שהטור שואף ל0 זה מספיק כדי להגיד שתנאי לייבניץ מתקיים והוא מתכנס בתנאי?
- (לא מתרגל/ת): לא. לשם כך תצטרך/י להראות גם ש-
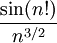 היא סדרה יורדת, מה שבוודאי אינו נכון. עם זאת, אפשר להראות שהטור מתכנס בהחלט:
היא סדרה יורדת, מה שבוודאי אינו נכון. עם זאת, אפשר להראות שהטור מתכנס בהחלט: 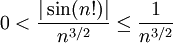 ובעזרת מבחן ההשוואה התכנסות הטור
ובעזרת מבחן ההשוואה התכנסות הטור 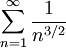 גוררת שהטור מתכנס.
גוררת שהטור מתכנס. 
כלל לופיטל
כאשר אני עושה את הנגזרת של המונה חלקי המכנה, מותר לי להתעסק עם השבר ולהעביר ביטויים מהמכנה למונה?
ואם נאי מעביר ביטויים מהמונה למכנה, כמו צמצום וכד' אז מותר לי להמשיך אחרי זה בגזירה?
- (לא מתרגל/ת): אחרי הגזירה - מותר, לפני - רק אם זה עדיין
 או
או 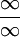 .
.
מבחן ההשוואה ה2
יוצא לי שאם ניקח לדוגמא: an = 1/n^2 ו bn = n אז נקבל שהחילוק בינהם הוא: an / bn = 1/n^3 והוא חסום בין 1 ל0. אזי אמורים להסיק שהטורים מתבדרים ביחד, מה שכמובן לא נכון.
אפשר קצת חידוד בנושא מבחן השוואה השני?
- לא יודע איך קיבלתם את מבחן ההשוואה בכיתה שלכם, אבל אצלנו (ד"ר הורוביץ) הוא ניתן כך:
אם 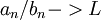 אז אם
אז אם 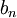 ∑ מתכנס אז
∑ מתכנס אז 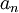 ∑ מתכנס. אם
∑ מתכנס. אם 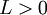 אז יתקיים שהטורים מתכנסים ומתבדרים יחד.
גרסה זו היא בהנתן טור חיובי.
מקווה שעזרתי! גל א.
אז יתקיים שהטורים מתכנסים ומתבדרים יחד.
גרסה זו היא בהנתן טור חיובי.
מקווה שעזרתי! גל א.
שאלה לגבי גבולות
מתי מותר לכתוב אם בכלל?
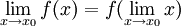
- (לא מתרגל/ת): כאשר f רציפה. שים/י לב שזה אותו דבר כמו
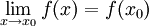 .
.
בשאלה ששואלים אותי  לא רציפה בהכרח ב
לא רציפה בהכרח ב 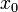
ומה קורה אם הפונקציה רציפה בכל הממשיים פרט ל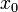
- (לא מתרגל/ת): אם היא לא רציפה ב-
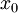 אז זה בהכרח לא נכון, כי אם
אז זה בהכרח לא נכון, כי אם 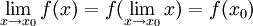 אז זה סותר את האי רציפות.
אז זה סותר את האי רציפות.
למה? הרי ש
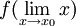 נותן את ערכי הפונקציה בסביבה של
נותן את ערכי הפונקציה בסביבה של 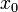 ולא את הערך ב
ולא את הערך ב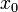 עצמו
עצמו
- (לא מתרגל/ת): לא.
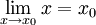 כי
כי 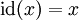 היא פונקציה רציפה ולכן
היא פונקציה רציפה ולכן 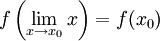 . את/ה כנראה מדבר/ת על
. את/ה כנראה מדבר/ת על 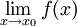 .
.
משפט רימן
לפי משפט רימן, שינוי סדרם של איבריו של טור מתכנס בתנאי יכול לשנות את המספר אליו מתכנס הטור או אפילו "לבדר" אותו. למרות זאת, כמה פעמים שינינו את סדרם של אינסוף איברים בטורים שאיננו יודעים אם הם מתכנסים (למשל פתרון שאלה 3 בתרגיל 7). מתי (אם בכלל) מותר לשנות את סדרם של אינסוף איברים בטור שלא ידוע שהוא מתכנס בהחלט?
- אסור לשנות את הסדר. מה שעשינו בתרגיל 3 הוא הפרדנו טור לכמה חלקים שונים, תוך שמירה על הסדר. מותר לעשות זאת מכיוון שאפשר לרפד באפסים (לפי למה שקל להוכיח). אסביר על ידי דוגמא: יהי
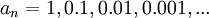 אזי לפי למה מותר לרפד במספר סופי של אפסים בין כל שני איברים וסכום הטור ישאר זהה, כלומר עבור
אזי לפי למה מותר לרפד במספר סופי של אפסים בין כל שני איברים וסכום הטור ישאר זהה, כלומר עבור 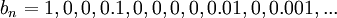 מתקיים
מתקיים 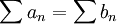 . כעת, ניתן לפצל באופן זה טור לשניים:
. כעת, ניתן לפצל באופן זה טור לשניים: 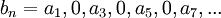 ו
ו 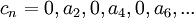 . בבירור, אם הטורים
. בבירור, אם הטורים 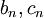 מתכנסים אזי
מתכנסים אזי 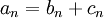 מתכנס. ולפי מה שאמרנו קודם, אפשר להעיף את האפסים ולהסתכל על הטורים
מתכנס. ולפי מה שאמרנו קודם, אפשר להעיף את האפסים ולהסתכל על הטורים 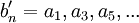 ו
ו 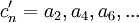 . כל זה מבלי לשנות את סדר האיברים כלל. --ארז שיינר 13:25, 26 בינואר 2011 (IST)
. כל זה מבלי לשנות את סדר האיברים כלל. --ארז שיינר 13:25, 26 בינואר 2011 (IST)
עזרה בפתרון שאלה
אפשר עזרה בהוכחת הטענה הבאה?: אם a_n_(k+1)-a_n_k שואף לאפס כשK שואף לאינסוף לכל ת"ס של an, אז an סדרת קושי. אני לא מצליח להוכיח את הטענה ואפילו לא מבין למה בהכרח היא נכונה! תודה לעוזרים
איפה זה חדר מחלקה שבו יתקיים שיעור חזרה ביום חמישי הקרוב??
- (לא מתרגל/ת):
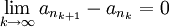 ולכן
ולכן 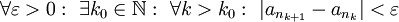 . זה נכון לכל תת סדרה של
. זה נכון לכל תת סדרה של 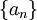 , כלומר לכל סדרה טבעית עולה ממש
, כלומר לכל סדרה טבעית עולה ממש 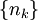 . לכן לכל m,n כך ש-m>n (בה"כ) נבחר סדרה
. לכן לכל m,n כך ש-m>n (בה"כ) נבחר סדרה 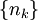 המקיימת
המקיימת 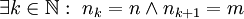 ולכן
ולכן 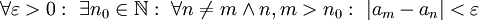 . אם m=n אז
. אם m=n אז 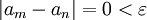 ולכן סדרת קושי.
ולכן סדרת קושי. 
- בקשר לחדר המחלקה, הוא נמצא בבניין 216 בחדר בקומה השנייה וכתוב על הדלת "חדר סטודנטים" (לא זוכר מה המספר).
- (לא אני שאלתי על החדר המחלקה, יש לשים את זה בכותרת נפרדת). אני לא בטוח שהפתרון הזה נכון, מכיוון שאני חושב שבפתרון הזה ה n0 תלוי ב-m ו-n, ואסור שתהיה תלות. תקנו אותי אם אני טועה?
- (לא מתרגל/ת): בקשר ל-
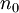 , זה בסדר כי אנחנו בוחרים את הסדרה ואת n0, ולכן אם n0 גדול מדי נבחר סדרה אחרת. ניסוח טוב יותר של אותו חלק של התשובה הוא: ... לכן לכל n0 ולכל m,n כך ש-m>n>n0 (בה"כ) נבחר סדרה
, זה בסדר כי אנחנו בוחרים את הסדרה ואת n0, ולכן אם n0 גדול מדי נבחר סדרה אחרת. ניסוח טוב יותר של אותו חלק של התשובה הוא: ... לכן לכל n0 ולכל m,n כך ש-m>n>n0 (בה"כ) נבחר סדרה 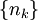 המקיימת
המקיימת 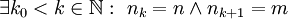 ולכן ... (שים לב שצריך לבחור n0>k כי אחרת לא קיימת סדרה טבעית עולה ממש כזו).
ולכן ... (שים לב שצריך לבחור n0>k כי אחרת לא קיימת סדרה טבעית עולה ממש כזו).
- אנחנו בוחרים את הn0, אבל אנחנו בוחרים אותו להיות משהו שקשור לn וm, כלומר אם נשאיר את אותו n0 ונשנה את הm והn, זה כבר לא נכון. (?)
- (לא מתרגל/ת): לא, ה-m וה-n נבחרים לפי n0 ולא להפך. ההוכחה שנתתי לא מלאה ונותנת רק את הרעיון הכללי, אבל בגלל ריבוי השאלות אני אכתוב את ההוכחה המלאה: מתקיים
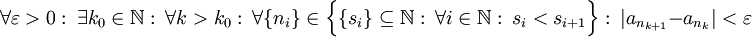 . לפיכך
. לפיכך 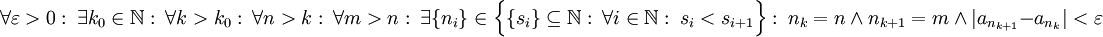 . מכאן נובע
. מכאן נובע 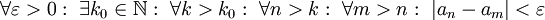 לכן
לכן 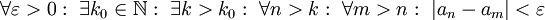 ולפיכך
ולפיכך 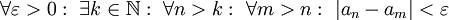 . לבסוף, m=n אז
. לבסוף, m=n אז 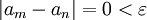 ולכן
ולכן 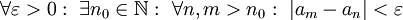 כלומר סדרת קושי
כלומר סדרת קושי  .
.
- (לא מתרגל/ת): לא, ה-m וה-n נבחרים לפי n0 ולא להפך. ההוכחה שנתתי לא מלאה ונותנת רק את הרעיון הכללי, אבל בגלל ריבוי השאלות אני אכתוב את ההוכחה המלאה: מתקיים
- אנחנו בוחרים את הn0, אבל אנחנו בוחרים אותו להיות משהו שקשור לn וm, כלומר אם נשאיר את אותו n0 ונשנה את הm והn, זה כבר לא נכון. (?)
- (לא מתרגל/ת): בקשר ל-
- (לא אני שאלתי על החדר המחלקה, יש לשים את זה בכותרת נפרדת). אני לא בטוח שהפתרון הזה נכון, מכיוון שאני חושב שבפתרון הזה ה n0 תלוי ב-m ו-n, ואסור שתהיה תלות. תקנו אותי אם אני טועה?
הוכחת אינדוקציה
נשמח אם תוכל להסביר למה הסדרה (2 בחזקת n) לחלק ל(n בחזקת 2)תמיד גדולה או שווה לאחד? (באינדוקציה)
- (לא מתרגל)-נניח לn, אזי
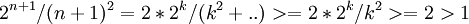 כשהשלב לפני אחרון לפני הנחת האינדוקציה.
כשהשלב לפני אחרון לפני הנחת האינדוקציה.
- (הלא ארז שיינר שענה אחריך): את/ה מתבלבל/ת.
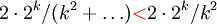 כי הקטנו את המכנה.
כי הקטנו את המכנה.
- (הלא ארז שיינר שענה אחריך): את/ה מתבלבל/ת.
- (לא ארז שיינר, אבל ביינתיים): הוספתי לאחר התנגשות עריכה -
ראשית נחשב את הביטוי ההופכי עבור 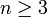 : :
|
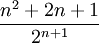
|

|
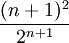
|
|||
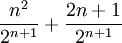
|

|
|||||
כאשר 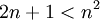 . פותרים ומקבלים . פותרים ומקבלים 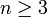 . .
|
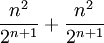
|
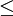
|
||||
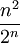
|

|
|||||
| הנחת האינדוקציה: | 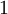
|
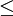
|
- נותר לבדוק עבור
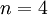 (עבור 3 לא מתקיים) ונקבל שלכל
(עבור 3 לא מתקיים) ונקבל שלכל 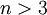 מתקיים
מתקיים 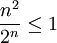 ולכן
ולכן 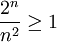 . בנוסף, בודקים עבור
. בנוסף, בודקים עבור 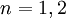 ... בדקנו. לבסוף לכל
... בדקנו. לבסוף לכל 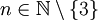 הטענה נכונה.
הטענה נכונה. 
מבחן באינפי
היי ארז,
איך נוכל לפתור 6 שאלות בשעתיים? זה ממש לא מספיק...ועוד יש בחירה מתוך 8...
האם יש אפשרות שיתנו לנו הארכה?
- המבחן הזה במתכונת הזו נעשה כבר עשרות שנים :) בכל אופן זו החלטה של זלצמן --ארז שיינר 13:14, 26 בינואר 2011 (IST)
- ובד"כ הוא לא נותן הארכה של חצי שעה בזמן המבחן, כמו אצל הורוביץ?
- אם אני לא טועה שנה שעברה הוא לא נתן, לא הייתי בונה על זה. תכוונו לפתור את המבחן בזמן הנתון --ארז שיינר 13:56, 26 בינואר 2011 (IST)
תרגילים
כאשר אני מנסה להיכנס לתרגילים,זה מחזיר אותי לדף הראשי של wiki.
מדוע?
תוכל להעלות שוב את הפתרונות של תרגילים 10-12 ותרגיל 13?
תודה!
- תנסה שוב, אולי תקלה זמנית. זה עובד... --ארז שיינר 13:13, 26 בינואר 2011 (IST)
פתרון מבחנים
האם יש אפשרות לעלות פתרונות למבחנים של זלצמן? לפחות את חלקם או תשובות מקוצרות?
תודה!!!!!!!
- אין פתרונות. אפשר לשאול שאלות ספציפיות פה, או להגיע לשיעורי חזרה או לצלם אותם, שם נפתרים לא מעט מבחנים. --ארז שיינר 13:15, 26 בינואר 2011 (IST)
פונקציה הפוכה
האם זה נכון שאם f רציפה אזי f חח"ע ולכן קיימת הפונקציה ההפוכה לf? אם כן אפשר הוכחה קצרה או רעיון כללי להוכחה? אולי צריך להוסיף את העובדה שFx>0 לכל x? תודה
- (לא מתרגל/ת): ממש לא (גם אם f(x)>0). הפונקצייה
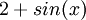 תמיד גדולה מ-0 וכן רציפה (כסכום של פונקציות רציפות) אבל בוודאי שאינה חח"ע. לעומת זאת, אם ב-F התכוונת ל-f' אז הטענה נכונה:
תמיד גדולה מ-0 וכן רציפה (כסכום של פונקציות רציפות) אבל בוודאי שאינה חח"ע. לעומת זאת, אם ב-F התכוונת ל-f' אז הטענה נכונה: 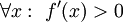 לכן לכל x1>x2 (בה"כ)
לכן לכל x1>x2 (בה"כ) 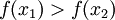 ובפרט
ובפרט 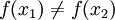 .
. 
עזרה בקביעת התכנסות טור
הטור של הסדרה 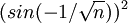 - האם הוא מתכנס בהחלט, בתנאי או מתבדר? אני לא מוצא אף מבחן או שום דבר לעשות עם הטור שעוזר לפתור. תודה מראש
- האם הוא מתכנס בהחלט, בתנאי או מתבדר? אני לא מוצא אף מבחן או שום דבר לעשות עם הטור שעוזר לפתור. תודה מראש
לא מתרגלת.. אבל תחל ב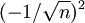
ואז על פי מבחן ההשואה של טורים חיוביים, בגלל שכאשר n שואף לאינסוף הגבול של מה שיצא הוא אחד הטורים מתכנסים ומתבדרים כאחד, ולכן בגלל שהטור שחילקנו בו מתבדר גם הטור הנתון מתבדר
- תודה
שאלה ממבחן
נתונה פונקציה F: כאשר X רציונלי זה X^3 כאשר X לא רציונלי זה 3X-2 צריך לבדוק איפה F רציפה ואיפה F גזירה.. מה הפתרון?
עוד שאלה, האם נכון להניח שאם פונקציה אינה רציפה בנקודה אז היא אינה גזירה שם?
- (לא ארז)- קודם כל, זה נכון שאינה רציפה היא אינה גזירה מכיוון שגזירה היא בפרט רציפה. לשאלה- כל עוד x^3 לא שווה ל 3x-2 יש נקודת אי רציפה ממין שני כי (אולי קשה להסביר את זה)- הפונקציה מתנהגת כמו פונקציית דיריכלה- לא יכול להיות שאחד מהגבולות החד צדדיים קיימים כי יש אינסוף נקודות רציונליות ואי רציונליות, והרי לקיחת תת סדרה של רציונליים או אי רציונליים תיתן הסדרה ששואפת לגבול x^3 או 3x-2 בהתאמה, שהם שונים (כאשר 3x-2!=x^3). נותרו רק הנקודות שבהן
3x-2=x^3 - מנסים לפתור את המשוואה, אם יש פתרונות אז בנקודות האלה הפונקציה רציפה, אם אין פתרון אז אין נקודות רציפות. גזירה- דומה. מקווה שעזרתי (ותקנו אותי אם יש לי טעויות!)
נגזרת arctan, arcsin, arccos
האם במבחן יש להוכיח את הנגזרות של arcsin וarctan או שמספיק לדעת למה זה שווה ע"פ מה שהוכחנו בכיתה?
למה שורש שלישי של X רציפה במ"ש בקטע [0,1] לא הבנו את זה בתרגול.. תודה!!
רציפות במ"ש
מדוע הפונקציה שורש שלישי של X רציפה במ"ש בקטע 0-1 ו: -1-0.. הסברת את זה בתרגול אבל לא הבנו.. תודה!!
תשובה: אפשר לראות שקיימים גבולות סופיים כאשר מציבים את קצות הקטע ולכן רציפה במ"ש...
שלבים לקביעת התכנסות טור
היי ארז,
מהם שלבי העבודה המומלצים לקביעת התכנסות בתנאי או בהחלט או התבדרות הטור?
בנוסף אם יש לי טור כלשהו כפול הטור מינוס 1 בחזקת n אזי אם הטור a_n מתכנס אזי המכפלה של שני הטורים תתכנס בהחלט?
אם הטור a_n מתבדר אזי מכפלת שני הטורים תתכנס בתנאי?
ואם הסדרה a_n תשאף לכל גבול ממשי ששונה מאפס, אזי הטור יתבדר?
תודה!
פונקציה מעריכית
אני לא מצליח להוכיח שהיא רציפה במידה שווה לפי ההגדרה של רצב"ש!
- (לא מתרגל/ת): זה בגלל שהיא לא רציפה במידה שווה... בקטע סופי היא כן רצב"ש, ואת זה קל להוכיח כי היא כמובן רציפה וחסומה. אם רוצים להוכיח לפי ההגדרה זה קצת יותר מסובך: יהי I קטע סופי ותהא
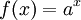 פונקציה מעריכית. כמו כן תהא
פונקציה מעריכית. כמו כן תהא 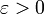 וצ"ל
וצ"ל 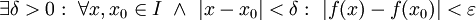 . עבור a>1:
. עבור a>1:
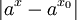
|

|
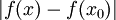
|
||||
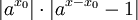
|

|
|||||
כמובן שאם M>x אז aM>ax. נסמן 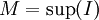 : :
|
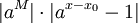
|
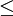
|
||||
בה"כ נאמר ש-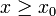 ולכן: ולכן:
|
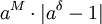
|
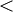
|
||||
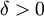 ולכן ולכן 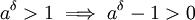
|
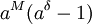
|

|
||||
נבחר 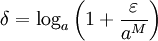 (אכן גדול מ-0 כי (אכן גדול מ-0 כי 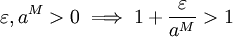 ) )
|

|

|
- לבסוף, אם 0<a<1 נתבונן בפונקציה a-x בקטע
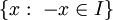 ואם a=1 הטענה בוודאי נכונה (במקרה הזה בלבד גם בקטע לא סופי) ונקבל שהטענה נכונה לכל a>0.
ואם a=1 הטענה בוודאי נכונה (במקרה הזה בלבד גם בקטע לא סופי) ונקבל שהטענה נכונה לכל a>0. 
אם ככה אז למה בפיתרון של המיבחן תרגיל 5 סעיפ c כתוב ש (e^(X^2 פונקציה רציפה במידה שווה?
סליחה טעות שלי זה פונקציה רציפה על פונקציה מחזורית תודה בכל מיקרה
log
כשהפונקציה log מופיעה במבחנים של זלצמן מתכוונים ללוג בבסיס 10 כפי שנהוג בד"כ או שהוא מתכוון לבסיס e?
ועוד שאלה לגבי התכנסות טורים- אם אני קובע שטור מסויים מתכנס, נניח לפי מבחן ההשוואה הראשון, הטור גדול שווה או קטן שווה מטור אחר אזי צריך להוכיח זאת באינדוקציה? כלומר, כל קביעה כזאת דורשת הוכחה באינדוקציה או הסבר נוסף?
- זלמן תמיד מתכוון לבסיס e. לגבי טורים, בדר"כ מראים שa_n<b_n באופן כללי ואין צורך באינדוקציה. זה תלוי מקרה עדיף לשאול את הבוחן. --ארז שיינר 10:37, 27 בינואר 2011 (IST)
שאלה על סדרות
אם נתון שסדרה a_n שואפת ל a. איך אפשר להוכיח שהסדרה a_n*a_n+1 שואפת ל a^2?
- אם אני מבין נכון, אז פשוט גם הסדרה a_n+1 גם מתכנסת לa (לא כמו בטורים- בסדרות הורדת מספר סופי של איברים מההתחלה לא תשנה בכלל את גבול הסדרה (וכמובן אם היא מתכנסת/מתבדרת)), וכעת לפי אריתמטיקה של גבולות הכפל המבוקש שואף ל a*a=a^2.
זה נכון,אבל איך אתה מוכיח שגם a_n+1 מתכנסת ל a?
- ברור, ידוע שזה יתכנס לאותו גבול. הגבול של סדרה לא מושפע מהאיברים הראשונים שלה אלא רק מ"האחרונים". (זה לא פורמלי אבל כדי שתבין). במילים אחרות, סופר קל להוכיח את זה- צ"ל שלכל אפסילון קיים N כך שבשבילו לכל n>N יקרה משהו. an+1 הוא אותו הטור כמו an רק שכל איבר זז אחורה והאיבר הראשון נעלם. לכן ניקח את הN החדש להיות N+1 הקודם, ואז אותו בשביל n+1 > N+1 יתקיים n>N ומכאן הסדרה תתכנס כמו הסדרה הראשונה.
שאלה ממבחן
an חיובית יורדת. צ"ל שאם הטור של a_5n מתכנס אז הטור (a_n) מתכנס. תודה!
- (לא מתרגל/ת): תהא
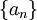 סדרה חיובית ויורדת כך ש-
סדרה חיובית ויורדת כך ש-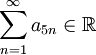 (כלומר מתכנס). מכיוון שהסדרה חיובית יורדת מתקיים
(כלומר מתכנס). מכיוון שהסדרה חיובית יורדת מתקיים 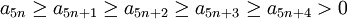 ולכן (ממבחן ההשוואה)
ולכן (ממבחן ההשוואה) 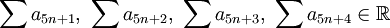 . כמו כן
. כמו כן 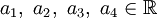 ולכן
ולכן 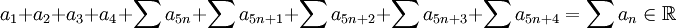 .
. 
- תודה!
תקלה באתר
הי ארז,
רבים מאיתנו חווים תקלה באתר, במסגרתה ההפניות מדפי הקורסים לדף השאלות והתשובות ולדף שיעורי הבית לא עובדים (וזה לא רק באינפי 1, זה גם למשל בלינארית 2). כדי להגיע לדף זה עלינו ללחוץ על הלשונית שיחה (בקורס זה, בלינארית 2 אפילו זה לא עובד) וכדי להגיע לשיעורי הבית עלינו להיכנס להיסטוריה של דף הקורס, ודרכה להיכנס להיסטוריה של דף שיעורי הבית ולהוריד ממנו את הקבצים. האם יש סיכוי שתוכל לטפל בזה? אמנם אני מודע לקשיים אלו, אבל רבים המשתמשים באתר עלולים לחוות בעיות עם השימוש בו, והבעיה בהצגת שיעורי הבית ממש מפריענ, אחרי הכל אנחנו צריכים אותם להתכוננות למבחן.
תודה, גל א.
- אני עכשיו שם לב שיש לי את הבעיה רק כשאני לא מחובר לאתר. גל.
מבחן
היי,
מי בודק את המבחן של התלמידים של זלצמן?
כמה אחוזים המבחן מהציון הכללי?
פרופ' זלצמן יהיה בבחינה?
מיבחן המנה
ברור שאם a_n+1/a_n <1 החל ממיקום מסוים זה מספיק בהחלט בישביל שהטור a_n שהוא טור חיובי יתכנס .האם זה תופס במיבחן או שצריך למיצוא את הגבול העליון?
- (לא מתרגל) לא מספיק, תבחן את הטור הההרמוני.
זיהוי וסיווג נקודות אי רציפות של הפונקציה
שלום,
האם עבור כל נק' אי רציפות שמצאתי, יש לבדוק את הגבול בסביבה הימנית והשמאלית של הגבול?
תודה!
- (לא מתרגל/ת): לא. אם זו נקודת אי-רציפות סליקה מספיק למצוא את הגבול הכללי. כמובן שבמקרה של נקודות אי-רציפות ממין ראשון או שני צריך.
מה מידת הדיוק שנדרשת בשאלות של גזירת פונקציות?
כלומר עד לאיזה ביטוי מצפים שנגיע בתשובה?
- (לא מתרגל) לפי מה שמבקשים בשאלה
- לא מתרגל אחר: אני חושב שהוא התכוון עד כמה צריך לצמצם איברים, לפתוח סוגריים וכו' - דבר שבד"כ לא מפורט בשאלות. אולי צריך מתרגל שיבהיר את העניין.
- כמה שאפשר, אם לא בטוחים אפשר לשאול בזמן המבחן. --ארז שיינר 13:55, 28 בינואר 2011 (IST)
- לא מתרגל אחר: אני חושב שהוא התכוון עד כמה צריך לצמצם איברים, לפתוח סוגריים וכו' - דבר שבד"כ לא מפורט בשאלות. אולי צריך מתרגל שיבהיר את העניין.
אי רציפות
בפונקציה (x*sin(1/x^2 האם זה נכון שב0 יש נק אי רציפות סליקה מיכיוון זאת פונקציה חסומה כפול פונקציה ששואפת לאפס ולכן הגבול בנק קיים ?תודה
תשובה: גם לי יצא ככה.
מועד ב' של שנה שעברה
ארז, יש מצב שאתה מעלה את המבחן מועד ב' של שנה שעברה, אפילו בלי פתרונות, לא הצלחתי למצוא אותו בשום מקום.
תודה.
- מצטער, אין לי. תנסו לבקש מהחברה של שנה שעברה --ארז שיינר 16:29, 28 בינואר 2011 (IST)