שיחה:88-211 תשעג סמסטר א/תרגילים

זה המקום לכל השאלות בנושא הקורס. הודעות תוכלו למצוא בדף הראשי של הקורס.

הנחיות

1. כשאתם מתייחסים לתרגיל, אנא צטטו.
2. אנא המנעו מלפתוח כותרות חדשות שלא לצורך.
3. חותמים בסוף כל הודעה באמצעות "~~~~. פתיחת חשבון - חינם.

תרגיל 1, שאלה 2, סעיף ה

בשאלה 2 ה יש צורך להוכיח אסוציאטיביות הפרש סימטרי? זה ארוך, מייגע ובאופן כללי לא נושא התרגיל.

כמובן שאין צורך להוכיח כי ההפרש הסימטרי הינו אסוציאטיבי. כבר הוכחתם את הטענה הזאת בבדידה... --לואי 18:42, 31 באוקטובר 2012 (IST)

שאלה

תרגיל שנתקלתי בו בחוברת של המרצה: תרגיל 1.1.8 אם 'f:X→X איזומורפיזם, אז f−1 (הפכי) גם הוא איזומורפיזם.

יש כאן שאלה? או סתם הגיגים?... =)--לואי 11:40, 29 באוקטובר 2012 (IST)

תרגיל 1, שאלה מס' 3

האם בתת הסעיף הראשון של א (וגם של סעיף ב' למעשה..) יש משמעות להאם זה מודולו 7 או לא? כי אחרת גם בא' וגם ב-ב' זאת בדיוק אותה תשובה, לא?!

כן... זה אותו הרעיון... --לואי 18:43, 31 באוקטובר 2012 (IST)

תרגיל 1 שאלה 5 סעיף ב'

בחבורה למחצה 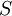$S$ יש 7 יחידות משמאל.

רק כדי לוודא, הכוונה היא ל-7 יחידות שונות זו מזו משמאל?

כן, יש 7 יחידות שונות משמאל. --לואי 21:03, 1 בנובמבר 2012 (IST)

תרגיל 1, שאלה 3

האם מותר להסתמך על האסוציטיבות במרוכבים, במקום לבדוק מחדש? אותו דבר לגבי ארבע, תודה.

• קודם כל - יפה ששמת לב לקשר עם המרוכבים! =)
• שנית, אני אענה באופן כללי: ניתן להסתמך של האסוציאטיביות של פעולות ידועות. למשל: הפעולות הבאות הן אסוציאטיביות ואין צורך להוכיח זאת מחדש: הפרש סימטרי, כפל מטריצות, כפל וחיבור ממשי/מרוכב, כפל וחיבור 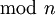$\mod n$ וכדומה. --לואי 21:09, 1 בנובמבר 2012 (IST)

תרגול כיתה (רגילים)- סתם הערה

בדוגמא הנגדית בשאלה האחרונה אפשר פשוט להגיד שהמטריצה ab שקיבלנו היא בעצם צורת ז'ורדן (עם ע"ע 1) ולכן לא ניתנת ללכסון ושונה מ I לכל n, נכון?! (במקום לתת לנו להוכיח את זה באינדוקציה =) )

לא בטוח שהבנתי את הטיעון. אני מסכים לכל המשפט :"שהמטריצה ab שקיבלנו היא בעצם צורת ז'ורדן (עם ע"ע 1) ולכן לא ניתנת ללכסון"

אבל לא ברור לי איך ממנו מסיקים(זאת אומרת בדרך השונה מאינדוקציה) שהמטריצה בחזקת n אינה I לכל n, על מה בדיוק הסתמכת? --מני 12:03, 8 בנובמבר 2012 (IST)

למעשה, הנה הטענה הכללית יותר: יהי 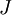$J$ בלוק ג'ורדן, אזי לכל 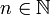$n\in \mathbb{N}$ מתקיים 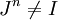$J^n \neq I$. למעשה, זהו תרגיל נחמד מאוד בליניארית.. נסו להוכיח =) אז אני מסכימה עם מני.. למרות שזה מסתבר להיות נכון, הקפיצה הלוגית שעשית היא לא כל כך טריוויאלית...--לואי 21:19, 8 בנובמבר 2012 (IST)

תרגיל 2, שאלה 4

עבור כל אחד מהסעיפים א-ג, האם יש צורך לדעת באיזה פעולת כפל מדובר? (כלומר, חבורה ביחס לאיזה פעולה?) אני מניח שמדובר על פעולת החיבור, לפחות בנוגע לסעיפים א,ב, אחרת היה מצויין כי מדובר בחבורה הכפלית, אבל מה בנוגע לסעיף ג'? יכול להיות שאני פשוט מפספס משהו מבחינת הבנה?

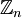$\mathbb {Z}_n$ ביחס לכפל אינו חבורה אף פעם. אפילו אם $n$ ראשוני שכן אין הופכי לאפס ביחס לכפל. לכן, יש טעם לדבר רק על החבורה החיבורית. הפעולה של שתי החבורות בשני הסעיפים א וב היא חיבור רכיב רכיב לפי מודולו n המתאים בכל רכיב.

לגבי סעיף ג' חבורת אוילר מוגדרת תמיד כחבורת ההפיכים של המונואיד 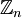$\mathbb {Z}_n$ ביחס לכפל.--מני 16:34, 8 בנובמבר 2012 (IST)

סילבוס

היי , איפה ניתן לקבל את הסילבוס של הקורס שיועבר ע"י פרופסור וישנה ? האם החומר יהיה תואם לחומר שנלמד ע"י ד"ר מגרל בקיץ ?

הסילבוס שווה לשמות הפרקים שבחוברת הקורס (יש קישור לאתר המרצה שם החוברת נמצאת). גרסה מפורטת: שמות הסעיפים פרט לאלו שכתוב עליהם שאפשר לדלג. לכל מרצה יש את הדגשים שלו. לכן, קשה להתחייב שהחומר יהיה תואם לקיץ אם כי פחות או יותר אמורים לכסות חומר דומה. --מני 10:39, 11 בנובמבר 2012 (IST)

תרגיל 2 שאלה 7 סעיף ב'

אפשר לקבל הסבר (דוגמה שלא קשורה לפתרון התרגיל תעזור גם כן) למה שנדרש?

(מישהו אחר) על אותו סעיף, מה פירוש 'שרשרת אינסופית (עולה)'? תודה

אתם יכולים לחשוב על סדרה של תתי חבורות. כך שהראשונה מוכלת ממש בשניה, השניה מוכלת ממש בשלישית וכו'. יש רמז לגבי התת חבורה הראשונה שאפשר לקחת. תנסו לחשוב אח"כ איך אתם יכולים למצוא תת חבורה של הרציונליים שמכילה ממש את הראשונה שבחרתם (יש יותר מאשר דרך אחת) וכך הלאה. אפשר לכל n טבעי להחליט מיהי התת חבורה בשלב הn שבחרתם ולהראות שהיא מכילה את זאת שנבחרה בשלב הקודם וכך לייצר את אותה שרשרת אינסופית עולה של תתי חבורות. --מני 19:48, 10 בנובמבר 2012 (IST)

תרגיל 2 שאלה6

כאשר יוצרים מונויד ציקלי האם צריך לדאוג שהאיבר שיוצר ייצור גם את איבר היחידה? או שהאיבר היחיד מוגד מראש להיות בתוך הקבוצה שהאיבר הנ"ל יוצר?

הוא יוצר את איבר היחידה בגלל שבדומה למצב בחבורה מגדירים

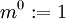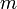$m^0:=1$ לכל $m$ במונואיד. בחבורה כשדיברנו על יוצר אז דיברנו גם על חזקות שליליות אבל במונואיד לא כל איבר צריך להיות הפיך אז יש טעם לדבר רק על חזקות אי שליליות ובתוכן גם חזקת אפס. --מני 22:39, 10 בנובמבר 2012 (IST)

איך מוצאים מונואיד כזה??? אני לא מצליח! רמז? כיוון, משהו?

רמז? אוקיי... בעיקרון, הרי אין בעיה ליצור משהו ציקלי, הבעיה היא איך מונעים מהמבנה הזה להיות חבורה... והפתרון הוא לדאוג לכך שאחד האיברים (היוצר?) לא יהיה הפיך... נסו לקחת מבנה קטן ולשחק עם טבלאות כפל... --לואי 21:55, 13 בנובמבר 2012 (IST)

פתרונות לתרגילים

אשמח אם תוכלו לפרסם פתרונות לתרגילים. תודה(:

תרגיל 3 שאלה 3 סעיף א

האם הכוונה בסעיף זה היא לתת דוגמה לכך שקוסט ימני שונה מקוסט שמאלי לגבי אותו איבר?

לא זאת כוונת השאלה. קוסטים שמאליים הם מחלקות שקילות וכאשר מגדירים פונקציה על מחלקות שקילות צריך להראות שאין תלות בנציג מהמחלקה שבחרנו כדי שהפונקציה תהיה בכלל מוגדרת היטב (לא שולחת אותו איבר ליותר ממקום אחד). בשאלה הכוונה למצוא דוגמא שבה כן יש תלות כזו. --מני 19:14, 17 בנובמבר 2012 (IST)

תרגיל 3 שאלה 7 סעיף ג'

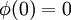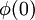האם $\phi(0)=0$?

$\phi(0)$ אינו מוגדר. עם זאת 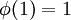$\phi(1)=1$, ובתרגיל המדובר הניחו ש- 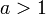$a>1$. --לואי 19:50, 17 בנובמבר 2012 (IST)

הערך 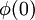$\phi(0)$ אכן אינו מוגדר, אבל אם היינו רוצים להגדיר אותו, הייתי בוחר בערך 2. נחזור על ההגדרה הכללית עבור n=0: "שקילות מודולו n" היא יחס השוויון, ולכן החבורה 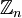$\ \mathbb{Z}_n$ עבור n=0 היא חבורת המספרים השלמים כולה. "חבורת אוילר" היא אוסף האברים ההפיכים בחבורה הזו (ביחס לכפל), כלומר המספרים 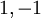$\ 1,-1$, שיש בה 2 אברים. אפילו משפט אוילר מתקיים (עבור n=0): לכל a "זר ל-0" (כלומר שווה ל-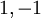$\ 1,-1$), מתקיים 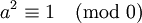$\ a^2 \equiv 1 \pmod{0}$. עוזי ו. 19:42, 18 בנובמבר 2012 (IST)