שיחה:88-211 תשעד סמסטר א/תרגילים
תוכן עניינים
- 1 תרגיל 1, שאלה 6
- 2 תרגיל 1 שאלה 5
- 3 שאלה כללית - תרגיל 3 שאלה 3
- 4 תרגיל 3, שאלה 2, סעיף ב'
- 5 המשך לשאלה שלי תרגיל 3 שאלה 3
- 6 שאלה תרגיל 3 סעיף א בשאלה 3
- 7 כפל של שתי מטריצות בתרגיל 2 שאלה 3
- 8 הסבר מדוע יש רק תת חבורה אחת מסדר 5 ב-D5
- 9 שאלה 1 א', תרגיל 5
- 10 שאלה 5 א', תרגיל 5
- 11 שאלה של התרגול הקודם וקשורה גם לתרגיל 7
- 12 המשפט הקטן של פרמה. כמה שאלות בנוגע לשלבים בהוכחה שלו
- 13 שאלה
- 14 תמורות
- 15 שאלה לגבי המושג "מוגדר היטב"
- 16 שאלה
- 17 עזרה בהוכחת הטענה הבאה:
- 18 תרגיל 9 שאלה 6
- 19 תרגיל 10 שאלה 4 סעיף א
- 20 תרגיל 11 שאלה 2
- 21 תרגיל 7 שאלה 6
תרגיל 1, שאלה 6
לגבי השאלה האחרונה, אני לא יודעת איך להוכיח את האיזומורפיות.
כלומר אני לא יודעת איזו פונקציה להגדיר כך שתתאים. גם איך לעשות אם אני לא יודעת מה זה (M,.)
הכוונה למונואיד הראשון שמופיע לא לשני.
אפשר לקבל כיוון? תודה
חשבתי אולי F(b)=ab
- תשובה:
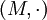 הוא מונואיד כלשהו, אנחנו גם לא צריכים לדעת מהו. באמצעות מונואיד זה, אנחנו מגדירים מונואיד חדש,
הוא מונואיד כלשהו, אנחנו גם לא צריכים לדעת מהו. באמצעות מונואיד זה, אנחנו מגדירים מונואיד חדש, 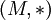 . האיברים שלו הם אותם האיברים, אבל הפעולה שונה. על מנת להוכיח שהם איזומורפיים, יש להגדיר פונקציה
. האיברים שלו הם אותם האיברים, אבל הפעולה שונה. על מנת להוכיח שהם איזומורפיים, יש להגדיר פונקציה 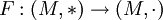 . הפונקציה הזאת צריכה להיות, קודם כל, הומומורפיזם (של מונואידים). כלומר היא צריכה לקיים
. הפונקציה הזאת צריכה להיות, קודם כל, הומומורפיזם (של מונואידים). כלומר היא צריכה לקיים 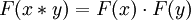 (שימו לב שהפעולה בשני האגפים היא שונה, בהתאם למונואיד שבו הפעולה מתבצעת).
(שימו לב שהפעולה בשני האגפים היא שונה, בהתאם למונואיד שבו הפעולה מתבצעת).
בנוסף, היא צריכה להעביר את איבר היחידה של המונואיד הראשון לאיבר היחידה של המונואיד השני. אז גם אם לא מצליחים מיד לנחש את הפונקציה, זהו מקום טוב להתחיל. היזכרו שבתרגול כבר הראינו מיהו איבר היחידה של 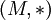 , אז תנסו לנחש פונקציה שתשלח אותו לאיבר היחידה של
, אז תנסו לנחש פונקציה שתשלח אותו לאיבר היחידה של 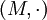 . --לואי 19:06, 21 באוקטובר 2013 (IDT)
. --לואי 19:06, 21 באוקטובר 2013 (IDT)
תרגיל 1 שאלה 5
בתרגיל מוגדר כפל ב-S כאשר S היא הקבוצה עליה מוגדרת הפעולה. אני משער שהכוונה היא לכפל ב-s (קטנה), אם לא אז אשמח לדעת כיצד מוגדר כפל של איבר בקבוצה בקבוצה עצמה.
אם זו אכן טעות מקלדת אז יש לי שאלה אחרת... אם נתבונן בקבוצה {0,1} ונגדיר שכפל כל שני איברים בה יתן 0 נקבל חבורה למחצה שמקיימת את תנאי השאלה אבל אינה מונואיד- היכן הטעות שלי?
תודה
- תשובה: זהו אכן כפל של איבר בכל הקבוצה, והוא מוגדר באופן הבא:
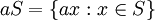 .--לואי 16:30, 22 באוקטובר 2013 (IDT)
.--לואי 16:30, 22 באוקטובר 2013 (IDT)
שאלה כללית - תרגיל 3 שאלה 3
אז רציתי לדעת באופן כללי,איך את מחשבת את איברי החבורה שנוצרים ע"י איברים מסוימים.למשל,בשאלה 3 של ש.ב האחרונים,אני לא כ"כ הבנתי את מצאת את האיברים בחבורה(שני הסעיפים בכלל).איך עושים כדי כדי למצוא איברי חבורה בחהורות סימטריה?
- תשובה: אז קודם כל את שואלת גם על סעיף א', ואני לא בטוחה שאני מבינה את השאלה.... לגבי סעיף ב': החישוב שנעשה שם הוא חישוב ישיר של כל המכפלות. כלומר, אנחנו יודעים שהאיברים בחבורה הנוצרת על-ידי
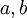 הם מהצורה
הם מהצורה 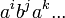 וכד'. אז קודם כל חישבנו את החזקות של כל אחד מהיוצרים (הראשון מסדר 2 והשני מסדר 3) ואז התחלנו להכפיל אותם (עם החזקות ובלי) משני הצדדים עד אשר ראינו שמיצינו את כל האפשרויות וניתן לעצור. כרגע, זו הדרך היחידה שלנו למצוא את האיברים בחבורות כאלה. --לואי (שיחה) 12:07, 11 בנובמבר 2013 (EST)
וכד'. אז קודם כל חישבנו את החזקות של כל אחד מהיוצרים (הראשון מסדר 2 והשני מסדר 3) ואז התחלנו להכפיל אותם (עם החזקות ובלי) משני הצדדים עד אשר ראינו שמיצינו את כל האפשרויות וניתן לעצור. כרגע, זו הדרך היחידה שלנו למצוא את האיברים בחבורות כאלה. --לואי (שיחה) 12:07, 11 בנובמבר 2013 (EST)
תרגיל 3, שאלה 2, סעיף ב'
מדוע מתקיים α^t=β^t =id? למה השיוון של החזקות מתקיים?
- תשובה: נניח שזה לא מתקיים. זה אומר ש-
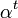 הוא ההופכי של
הוא ההופכי של 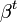 . אבל שימו לב שזה לא אפשרי, כי אם
. אבל שימו לב שזה לא אפשרי, כי אם 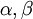 זרים, אז גם כאשר מעלים אותם בחזקה הם נשארים זרים. ומחזורים זרים אינם יכולים להיות הופכי אחד של השני, שכן ההופכי של מחזור
זרים, אז גם כאשר מעלים אותם בחזקה הם נשארים זרים. ומחזורים זרים אינם יכולים להיות הופכי אחד של השני, שכן ההופכי של מחזור 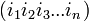 הוא
הוא 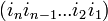 .--לואי (שיחה) 12:03, 11 בנובמבר 2013 (EST)
.--לואי (שיחה) 12:03, 11 בנובמבר 2013 (EST)
המשך לשאלה שלי תרגיל 3 שאלה 3
סימני הדולר האלה עושים לי שחור בעיניים...בעצם את אומרת שמתקיים: α=(145)(263) וגם עבור β=(15)(36) אזי:
α^3=id
β^2=id
שזה נכון,אני מסכימה. אבל גם מחשבים בנוסף
β,α,α^2,αβ,α^2*β,?
- תשובה: כן, מחשבים את כל האפשרויות האלה... ובקשר לסימני הדולר: ניסית לפתוח את האתר בדפדפן שונה? --לואי (שיחה) 06:49, 12 בנובמבר 2013 (EST)
שאלה תרגיל 3 סעיף א בשאלה 3
איך להסביר שהדוגמה לאיזומורפיזם זה אכן איזומורפיזם?זה לא טריוויאלי מכיוון שלכל איבר מתאים איבר אחר וכדומה?
בעצם לא משנה הבנתי למה.על זה טריוויאלי וזה חח"ע כי בהרכבה שתי החבורות או קבוצות לצורך העניין הן מסדר סופי עם מספר זהה של איברים
- תשובה: דווקא יש להסביר משהו אחר ממה שציינתם. נסמן לרגע את האיברים של חבורת קליין ב-
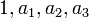 . ברור שהפונקציה שהגדרנו היא חח"ע ועל, אבל זה לא מספיק. מה שצריך להראות (ודווקא בכלל לא ברור מההגדרה של הפונקציה) זה שהיא למעשה הומומורפיזם. כלומר, יש להראות שמתקיים
. ברור שהפונקציה שהגדרנו היא חח"ע ועל, אבל זה לא מספיק. מה שצריך להראות (ודווקא בכלל לא ברור מההגדרה של הפונקציה) זה שהיא למעשה הומומורפיזם. כלומר, יש להראות שמתקיים 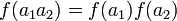 וכד'. --לואי (שיחה) 13:16, 15 בנובמבר 2013 (EST)
וכד'. --לואי (שיחה) 13:16, 15 בנובמבר 2013 (EST)
כלומר לדוגמה שמתקיים:
f((13)(24))* f((14)(23))=35=3(mod8 f((13)(24)(14)(23))=f((12)(34))=3(mod8
נכון?
- כן
כפל של שתי מטריצות בתרגיל 2 שאלה 3
האם אפשר לעשות את זה כך בסעיף א כדי להראות כי G תת חבורה?
ראינו את הכפל של שתי מטריצות שנמצאות ב-G בתרגיל 1 שאלה 4 וכמו כן גם את ההופכי. האם אפשר להסביר כי כל אחד מהאיברים שמעל האלכסון הראשי שייך ל-Zֹ3 כי שלוש האפשרויות לבחירת המספרים האלה (נניח d+a( תמיד תביא לכך שהסכום של זה יהיה 0 או 1 או 2 וכך הלאה? וכמובן לעשות זאת גם בהופכי?
- מקווה שהבנתי את השאלה, אם כי לא בטוח. אכן ראינו את רוב התכונות כבר בתרגיל 1. כדי להסביר שרכיבי המטריצות (לאחר מכפלה והיפוך) נמצאים ב-
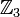 מספיק לומר שזו חבורה, ולכן סגורה לפעולה ולהופכי (הנגדי, במקרה של ההופכי שלנו). --לואי (שיחה) 05:23, 18 בנובמבר 2013 (EST)
מספיק לומר שזו חבורה, ולכן סגורה לפעולה ולהופכי (הנגדי, במקרה של ההופכי שלנו). --לואי (שיחה) 05:23, 18 בנובמבר 2013 (EST)
הסבר מדוע יש רק תת חבורה אחת מסדר 5 ב-D5
הסבר הולם שאפשר לתת לכך שתת החבורה הנוצרת ע"י סיגמה היא היחידה מסדר 5 היא מכיוון שמיצינו את שאר האפשרויות?כלומר אין תת חבורה מסדר 5 עם איבר מהצורה של תאו סיגמה בחזקת ג"י כלשהו כי הם איברים של תת חבורות מסדר 2?
- כדי שתהיה לנו תת חבורה ציקלית מסדר 5, צריך שיהיה איבר מסדר 5. אבל כל האיברים מסדר 5 כבר נמצאים בתת החבורה שמצאנו (זו שנוצרת על-ידי הסיבוב).--לואי (שיחה) 02:38, 25 בנובמבר 2013 (EST)
שאלה 1 א', תרגיל 5
מדוע מתקיים
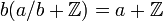 זה לא אמור להיות שווה ל-
זה לא אמור להיות שווה ל-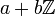 ? שכן
? שכן 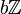 אמורה להיות תת חבורה לא אבל אין שיווין ממש...
אמורה להיות תת חבורה לא אבל אין שיווין ממש...
- תשובה: שימו לב שזו לא פתיחת סוגריים! זו פעולה בחבורת המנה! זה כתוב בכתיב חיבורי, אך בכתיב כפלי זה שקול ל:
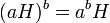 . כלומר, לא מעלים גם את
. כלומר, לא מעלים גם את 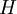 בחזקה, כי לא כך מוגדרת הפעולה על איברי חבורת המנה. --לואי (שיחה) 04:40, 1 בדצמבר 2013 (EST)
בחזקה, כי לא כך מוגדרת הפעולה על איברי חבורת המנה. --לואי (שיחה) 04:40, 1 בדצמבר 2013 (EST)
שאלה 5 א', תרגיל 5
לא הבנתי את המניע לאיזומורפיות של
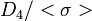 ל-
ל- 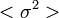 . האם זה נובע כי שתיהן מסדר 2?
. האם זה נובע כי שתיהן מסדר 2?
- תשובה: בדיוק! הן מסדר 2, וכפי שמצויין בסוגריים - יש רק חבורה אחת (עד כדי איזומורפיזם) מסדר 2. --לואי (שיחה) 04:40, 1 בדצמבר 2013 (EST)
אם נניח הייתי רוצה להשתמש במשפט האיזומורפיזם השלישי , אז איך נעשה?
הכוונה שלי לאיזומורפיות שאלה 5 סעיף א
- תשובה: בקשר לאיזומורפיזם שלישי, אולי התכוונת לאיזומורפיזם ראשון? אחרת אני לא מבינה את השאלה. ואם אכן הכוונה לאיזומורפיזם ראשון, אז מה השאלה? האם השאלה היא איך בונים את האיזומורפיזם?...--לואי (שיחה) 09:01, 3 בדצמבר 2013 (EST)
לא כ"כ הבנתי מה הפירוש של חבורה יחידה עד כדי איזומורפיזם...
למה מה שקיבלנו לא יכול להיות איזומורפי ל-Z2 למשל?
- תשובה: "חבורה יחידה עד כדי איזומורפיזם" אומר שכל החבורות מסדר 2 איזמורפיות זו לזו. דוגמה נוספת לשימוש בביטוי זה: "יש שתי חבורות מסדר 6 עד כדי איזומורפיזם". הוכחנו שאכן יש רק 2, שהן הדיהדרלית והציקלית מסדר 6. אז למעשה הוכחנו שאם יש לנו חבורה מסדר 6, אז היא איזומורפית לאחת מהשתיים האלה. ובחזרה לשאלה: מה שקיבלנו כבר איזומורפי ל-
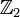 , אז בטח שהוא "יכול להיות איזומורפי ל...". --לואי (שיחה) 09:01, 3 בדצמבר 2013 (EST)
, אז בטח שהוא "יכול להיות איזומורפי ל...". --לואי (שיחה) 09:01, 3 בדצמבר 2013 (EST)
חשבתי על משפט האיזומורפיזם השלישי כי ראיתי באתר שנת תשע"ב בתרגילי כיתה איך אפשר להוכיח למשל שמתקיים ש-Z2 איזומורפי למנה של Z6/3Z6 באמצעות איזו 3.אז רציתי לדעת באופן אם אפשר לעשות זאת כאן.אך אם את אומרת שאפשר בעזרת איזו 1 אז איך את יכולה להוכיח שאכן מתקיים האיזומורפיות הזאת כלומר איך תבני אותו כן :)
- תשובה: אז קודם כל, אפשר לקבל הפניה לסיכומי ההרצאות האלה של שנת תשע"ב? כי אני ממש לא מבינה מה עושה שם איזו' 3!... לגבי איך עושים את זה דרך איזו' 1: נגדיר הומומורפיזם
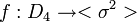 על-ידי (למשל)
על-ידי (למשל) 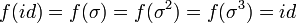 ואת שאר האיברים נשלח ל-
ואת שאר האיברים נשלח ל-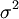 . קל לראות שהגרעין הוא בדיוק
. קל לראות שהגרעין הוא בדיוק 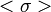 ולפי איזו' 1 מתקיים הדרוש. --לואי (שיחה) 09:09, 4 בדצמבר 2013 (EST)
ולפי איזו' 1 מתקיים הדרוש. --לואי (שיחה) 09:09, 4 בדצמבר 2013 (EST)
- המשך תשובה: קודם כל, זה צריך להיות "
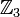 איזומורפי ל-
איזומורפי ל-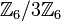 " ולא
" ולא 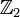 . שנית, זו לא הוכחה, אלא דרך להראות איך "מציבים" דברים בתוך משפט איזו' 3. שכן כל שלב בתוך ההצבה הזאת דורש הוכחה נפרדת (רוב השלבים לפי איזו' 1). --לואי (שיחה) 04:17, 5 בדצמבר 2013 (EST)
. שנית, זו לא הוכחה, אלא דרך להראות איך "מציבים" דברים בתוך משפט איזו' 3. שכן כל שלב בתוך ההצבה הזאת דורש הוכחה נפרדת (רוב השלבים לפי איזו' 1). --לואי (שיחה) 04:17, 5 בדצמבר 2013 (EST)
שאלה של התרגול הקודם וקשורה גם לתרגיל 7
הייתה שאלה בתרגול כאשר דיברנו על מחלקות צמידות, למצוא את מספר התמורות הצמודות ל- (78)(56)(1234) וכתבת שהתשובה הינה (1 2)(2 4)*3!(4 8) כל זה כפול חצי. אז כנראה לא הבנתי למה הכפל ב3! והחילוק בשתיים
- תשובה: אז קודם צריך לבחור מחזור באורך 4. יש 8 מעל 4 אפשרויות לבחור ארבעה מספרים, ואז צריך לסדר אותם במעגל (כי תמורה זה כמו מעגל: מתקיים
(1234)=(2341)=(3412)=(4123)...)
ובאופן כללי יש 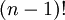 דרכים לסדר
דרכים לסדר  פריטים במעגל.
לגבי "חלקי 2": זה בגלל שאין חשיבות לסדר של המחזורים מאורך 2, כי מבחינת הצמידות, הם נמצאים באותה מחלקה. --לואי (שיחה) 03:39, 9 בדצמבר 2013 (EST)
פריטים במעגל.
לגבי "חלקי 2": זה בגלל שאין חשיבות לסדר של המחזורים מאורך 2, כי מבחינת הצמידות, הם נמצאים באותה מחלקה. --לואי (שיחה) 03:39, 9 בדצמבר 2013 (EST)
המשפט הקטן של פרמה. כמה שאלות בנוגע לשלבים בהוכחה שלו
המשפט הקטן של פרמה אומר שלכל מספר ראשוני 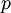 ולכל מספר שלם
ולכל מספר שלם 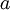 מתקיים:
מתקיים:
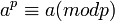 וזה שקול ללהגיד:
וזה שקול ללהגיד: 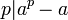 .
.
הוכחה:
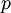 ראשוני ולכן
ראשוני ולכן 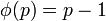 .
.
(אני רוצה לוודא שהבנתי למה השורה האחרונה נכונה:
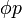 מוגדר להיות מספר המספרים הטבעיים שקטנים ממש מ-
מוגדר להיות מספר המספרים הטבעיים שקטנים ממש מ-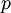 ושזרים ל-
ושזרים ל-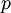 .
.
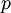 ראשוני ולכן כל המספרים שקטנים ממנו, זרים לו.
ראשוני ולכן כל המספרים שקטנים ממנו, זרים לו.
למשל עבור 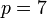 נקבל ש-
נקבל ש- 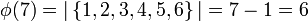 .
.
האם הבנתי נכון?)
המשך הוכחה:
לכן 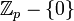 היא מסדר
היא מסדר 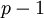 .
.
(שאלה: 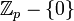 היא חבורה ביחס לכפל מודולו
היא חבורה ביחס לכפל מודולו 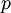 או חיבור מודולו
או חיבור מודולו 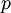 ??? )
??? )
המשך הוכחה:
לפי משפט אוילר, אם 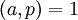 אז
אז 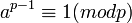 .
.
לאחר כפל שניי אגפי המשוואה ב-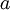 יוצא ש
יוצא ש
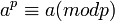 כאשר
כאשר 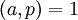 .
.
איך ממשיכים את ההוכחה עבור המקרה ש- 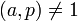 ????
????
- הפעולה בחבורת אוילר היא כפל (
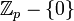 אינה סגורה לחיבור!). אי אפשר להשתמש במשפט אוילר כדי להוכיח את משפט פרמה, שקדם לו במאה שנים. ההוכחה (של שניהם) היא להפעיל את משפט לגרנז' על חבורת אוילר מהסדר המתאים.
אינה סגורה לחיבור!). אי אפשר להשתמש במשפט אוילר כדי להוכיח את משפט פרמה, שקדם לו במאה שנים. ההוכחה (של שניהם) היא להפעיל את משפט לגרנז' על חבורת אוילר מהסדר המתאים. - במקרה ש-a אינו זר ל-p, בהכרח p מחלק את a ולכן p מחלק כל חזקה של a וממילא גם את ההפרש a^p-a. עוזי ו. (שיחה) 12:17, 21 בדצמבר 2013 (EST)
שאלה
בהינתן חבורה G ותת חבורה H, מתקיים שכל המחלקות של H הן שוות עוצמה? כלומר הן מאותו סדר?
- כן -- כל הקוסטים של H הם מאותו סדר. הסיבה היא ש-
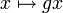 מהווה איזומורפיזם של קבוצות מ-H ל-gH. עוזי ו. (שיחה) 12:20, 21 בדצמבר 2013 (EST)
מהווה איזומורפיזם של קבוצות מ-H ל-gH. עוזי ו. (שיחה) 12:20, 21 בדצמבר 2013 (EST)
תמורות
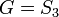 .
.
כלומר ב-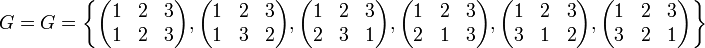
למה 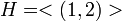 היא תת חבורה של
היא תת חבורה של 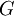 ? למה זו בכלל תת קבוצה של
? למה זו בכלל תת קבוצה של 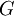 ???
???
מי האיברים של 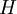 ???
???
- יש שתי דרכים לסמן תמורה: אחת באופן מפורש כפי שמנית לעיל, והשניה כמכפלה של מחזורים זרים. כשכותבים (12) הכוונה היא לתמורה המעבירה את 1 ל-2, את 2 ל-1, ואת 3 ל-3. עוזי ו. (שיחה) 12:21, 21 בדצמבר 2013 (EST)
שאלה לגבי המושג "מוגדר היטב"
בהינתן חבורה 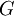 ותת חבורה
ותת חבורה 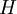 , מגדירים את חבורת המנה
, מגדירים את חבורת המנה
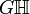 שהיא אוסף הקוסטים השמאליים של
שהיא אוסף הקוסטים השמאליים של 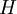 ב-
ב-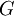 .
.
כעת, רוצים להגדיר פעולה על האיברים באוסף הזה (שהאיברים האלה הם למעשה קבוצות).
בחרו להגדיר את הפעולה כך: עבור שניי איברים בחבורת המנה: 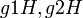 מגדירים פעולה באופן הבא:
מגדירים פעולה באופן הבא:
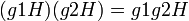 .
.
כעת שואלים האם הכפל הזה מוגדר היטב.
יש לי כמה שאלות:
1. לא הבנתי מה זה אומר בכלל המושג "מוגדר היטב".
2. באילו מצבים צריך לבדוק האם פעולה "מוגדרת היטב".
3. למה חשוב לבדוק האם פעולה "מוגדרת היטב".
4. מבחינה טכנית, איך בודקים האם פעולה מוגדרת היטב? למשל בשאלה הספציפית הזו, איך אני מוכיח שפעולה מוגדרת היטב? קראתי את ההוכחה מההרצאה ואני לא מבין ממנה שום דבר.
אודה על העזרה.
- הטענה שמשהו "מוגדר היטב" פירושה שההגדרה שלפנינו היא תקינה. יש לבדוק זאת *עבור כל הגדרה*, אלא שבדרך כלל הבדיקה כל-כך טריוויאלית עד שאין מזכירים אותה. לדוגמא, כשמגדירים פונקציה מ-X ל-Y, יש לבדוק שהתהליך המחשב את התמונה פועל לכל x ב-X (אין "חילוק באפס" או צרות דומות), שהוא לא תלוי בהטלת קוביה או בחירות אחרות שעושים בדרך, ושהוא אכן נותן איבר של Y. אם הבדיקה הזו נכשלת, פירושו של דבר הוא שאנחנו *אומרים* שהגדרנו, אבל זה פשוט לא נכון. במקרה של כפל מחלקות, שים לב שהנוסחה הנתונה משתמשת בנציגים --- אבל כל מחלקה אפשר להציג על-ידי נציגים שונים, ולכן יש לבדוק שהחלפת הנציגים אינה משנה את התשובה.
- (מה שקראת אינו ההוכחה מההרצאה בשלמותה, אלא ההעתקה החלקית שלה למחברת של אחד הסטודנטים). עוזי ו. (שיחה) 12:26, 21 בדצמבר 2013 (EST)
שאלה
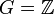 ו-
ו- 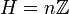 .
.
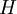 תת חבורה נורמלית של
תת חבורה נורמלית של 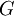 כי
כי 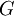 אבלית.
אבלית.
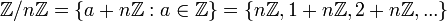
לכן האיברים בחבורה 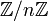 הם מהצורה:
הם מהצורה:
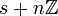 כאשר
כאשר 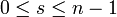 .
.
כעת, מבצעים פעולת חיבור על שניי איברים 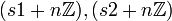 של חבורת המנה
של חבורת המנה 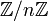 .
.
מה שלא ברור לי זה למה תוצאת החיבור היא: 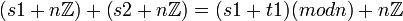
ולא 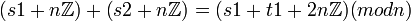
??
לא אמורים לחבר ובסוף, על התוצאה של החיבור הרגיל, לעשות מודולו  ?
?
ושאלה שנייה:
למה 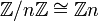
- תרגיל: הוכח ש-
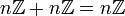 (ולא
(ולא 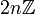 ). מדובר כאן בחיבור קבוצות, המוגדר כקבוצת כל הערכים שאפשר לקבל מסיכום נציג מכל קבוצה.
). מדובר כאן בחיבור קבוצות, המוגדר כקבוצת כל הערכים שאפשר לקבל מסיכום נציג מכל קבוצה. - לשאלה השניה: אני מניח שהכוונה היא ל-
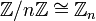 . זוהי דוגמא פשוטה למשפט האיזומורפיזם הראשון. עוזי ו. (שיחה) 13:30, 21 בדצמבר 2013 (EST)
. זוהי דוגמא פשוטה למשפט האיזומורפיזם הראשון. עוזי ו. (שיחה) 13:30, 21 בדצמבר 2013 (EST)
עזרה בהוכחת הטענה הבאה:
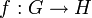 איזומורפיזם אם ורק אם קיימת העתקה
איזומורפיזם אם ורק אם קיימת העתקה
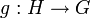 כך שמתקיים:
כך שמתקיים:
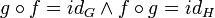 .
.
אפשר עזרה בהוכחה הזו. האמת זה נראה לי משפט שקשור לנושא של פונקציות מבדידה. איך אני מוכיח את זה?
- ראשית, יש לתקן את הטענה תיקון קל:
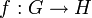 הוא איזומורפיזם אם ורק אם קיים הומומורפיזם
הוא איזומורפיזם אם ורק אם קיים הומומורפיזם 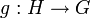 כך שמתקיים...". בבדידה מוכיחים טענה דומה: "פונקציה
כך שמתקיים...". בבדידה מוכיחים טענה דומה: "פונקציה 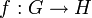 היא חד-חד-ערכית ועל אם ורק אם קיימת פונקציה
היא חד-חד-ערכית ועל אם ורק אם קיימת פונקציה 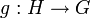 כך שמתקיים:
כך שמתקיים: 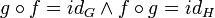 ". עוזי ו. (שיחה) 12:31, 21 בדצמבר 2013 (EST)
". עוזי ו. (שיחה) 12:31, 21 בדצמבר 2013 (EST)
תרגיל 9 שאלה 6
בפתרון לשאלה 6 רשום כי 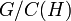 היא חבורה מסדר חזקת p. לכן
היא חבורה מסדר חזקת p. לכן 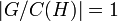 .
.
אפשר בבקשה הסבר לשורה זו.
תודה
- החבורה המקורית
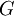 היא חבורת
היא חבורת 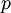 ולכן גם חבורת מנה שלה היא חבורת
ולכן גם חבורת מנה שלה היא חבורת 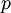 . מצד שני, חבורת המנה
. מצד שני, חבורת המנה 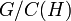 משוכנת בחבורת אוטומורפיזמים מסדר
משוכנת בחבורת אוטומורפיזמים מסדר 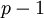 , מה שאומר שהסדר שלה,
, מה שאומר שהסדר שלה, 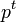 כלשהו, חייב לחלק את
כלשהו, חייב לחלק את 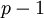 . האפשרות היחידה לכך היא במצב
. האפשרות היחידה לכך היא במצב 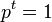 . --לואי (שיחה) 07:47, 23 בינואר 2014 (EST)
. --לואי (שיחה) 07:47, 23 בינואר 2014 (EST)
תרגיל 10 שאלה 4 סעיף א
בפתרון התרגיל נכתב כי לפי משפט האיזומורפיזם השני ![[H:H\cap\ K]=[HK:K]](/images/math/3/1/e/31edde85ac4c5fba74f79929fa5f660f.png) .
.
האם אנו יודעים כי 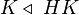 ?
?
או שזה לא נכון ולא נחוץ?
- זה לא נחוץ. העניין הוא שמאיזומורפיזם שני אנו מקבלים את הטענה האנלוגית
![[K:H\cap\ K]=[HK:H]](/images/math/5/f/1/5f1ef8838188449ee700b251857524a4.png) . לאחר מכן מקבלים את הטענה הכתובה בפתרון באמצעות כפליות האינדקס. --לואי (שיחה) 05:55, 24 בינואר 2014 (EST)
. לאחר מכן מקבלים את הטענה הכתובה בפתרון באמצעות כפליות האינדקס. --לואי (שיחה) 05:55, 24 בינואר 2014 (EST)
ז"א שלא בהכרח 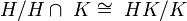 משום שאנו לא יודעים כי
משום שאנו לא יודעים כי 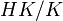 בכלל קיימת?
בכלל קיימת?
- בדיוק כך! כחבורות זה לא מוגדר, אבל כאינדקסים (הראנו את זה, נדמה לי, בתרגיל בית 6) השוויון כן מתקיים. --לואי (שיחה) 07:28, 24 בינואר 2014 (EST)
תרגיל 11 שאלה 2
בפתרון השאלה הגדרנו:
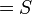 אוסף תת-חבורות p-סילו של G
אוסף תת-חבורות p-סילו של G
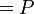 תת-חבורת p-סילו כלשהי של G
תת-חבורת p-סילו כלשהי של G
ואז נדרשנו להתבונן בפעולה 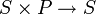 על ידי הצמדה.
על ידי הצמדה.
לא הצלחתי להבין מי היא החבורה הפועלת ומהו אופי הפעולה.
- יש לך טעות בהעתקה.. יכול להיות שזו הבעיה?... הפעולה היא לא
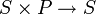 אלא
אלא 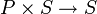 . החבורה הפועלת היא חבורת p-סילו כלשהי
. החבורה הפועלת היא חבורת p-סילו כלשהי 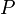 , והיא פועלת על אוסף של תת חבורות p-סילו על-ידי הצמדה. כלומר, היא לוקחת תת חבורה כלשהי
, והיא פועלת על אוסף של תת חבורות p-סילו על-ידי הצמדה. כלומר, היא לוקחת תת חבורה כלשהי 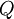 ומחזירה
ומחזירה 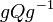 עבור
עבור 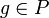 כלשהו. --לואי (שיחה) 12:55, 28 בינואר 2014 (EST)
כלשהו. --לואי (שיחה) 12:55, 28 בינואר 2014 (EST)
נכון, טעות שלי. תודה!
תרגיל 7 שאלה 6
אפשר בבקשה לקבל הסבר- למה יש 2^3 אפשרויות עבור סיגמא בריבוע/ טאו/ וכו...? לא הבנתי את החישוב... תודהה:)
- כנראה שציור יעזור כאן הרבה יותר, אבל ננסה. למשל לגבי השיקוף
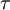 , הוא "מזהה" שני קודקודים עליונים ושני קודקודים תחתונים של הריבוע. יש שלושה צבעים, שני הקודקודים העליונים צריכים להיות צבועים באותו הצבע (כי השיקוף מעביר אחד מהם לשני) ולכן יש 3 אפשרויות לבחירת צבע עבור שני קודקודים אלה. כנ"ל לגבי הקודקודים התחתונים. לכן יש
, הוא "מזהה" שני קודקודים עליונים ושני קודקודים תחתונים של הריבוע. יש שלושה צבעים, שני הקודקודים העליונים צריכים להיות צבועים באותו הצבע (כי השיקוף מעביר אחד מהם לשני) ולכן יש 3 אפשרויות לבחירת צבע עבור שני קודקודים אלה. כנ"ל לגבי הקודקודים התחתונים. לכן יש 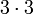 אפשרויות סה"כ עבור השיקוף.--לואי (שיחה) 05:51, 19 בפברואר 2014 (EST)
אפשרויות סה"כ עבור השיקוף.--לואי (שיחה) 05:51, 19 בפברואר 2014 (EST)