הבדלים בין גרסאות בדף "שיחה:89-214 סמסטר א' תשעב/תרגילים"
(←שאלות לקראת הבחינה) |
(←בניית שדה מסדר 27) |
||
| שורה 41: | שורה 41: | ||
== בניית שדה מסדר 27 == | == בניית שדה מסדר 27 == | ||
| − | '''שאלה'''. | + | '''שאלה'''. הוכח שקיים שדה מסדר 27. |
| − | '''פתרון'''. נתבונן בפולינום <math>\ x^{27} - x</math> מעל השדה <math>\ F=\mathbb{Z}_3</math>. הוכחנו שיש שדה המפצל את הפולינום הזה, ובתוך אותו שדה, אוסף השורשים של הפולינום מהווה שדה מסדר 27 | + | '''פתרון'''. נתבונן בפולינום <math>\ x^{27} - x</math> מעל השדה <math>\ F=\mathbb{Z}_3</math>. הוכחנו שיש שדה המפצל את הפולינום הזה, ובתוך אותו שדה, אוסף השורשים של הפולינום סגור לחיבור וכפל, ולכן הוא מהווה שדה מסדר 27. |
| − | הוכחנו שאם f הוא פולינום אי-פריק מעל F, אז חבורת המנה <math>\ K=F[x]/F[x]f(x)</math> היא שדה, שממדו המעלה של f. עלינו למצוא, אם כך, פולינום ממעלה 3 מעל השדה F. לפולינומים מהצורה <math>\ x^3 - a</math> יש שורשים (ולכן אינם פריקים); נבחר את הפולינום <math>\ f(x) = x^3-x+1</math>. עבור הפולינום הזה, K כולל את השאריות של כל הפולינומים מהצורה <math>\ a+bx+cx^2</math> (שמספרם כמובן 27), ופעולת הכפל מקיימת את החוק <math>\ x^3 = x-1</math> (ב-K). החבורה הכפלית של K היא ציקלית מסדר 26 (החבורה הכפלית של כל שדה סופי היא ציקלית). לכן תת-החבורה מסדר 13 היא זו הכוללת את כל הריבועים של אברים ב-K, ובפרט היא נוצרת (כפלית) על-ידי <math>\ x^2</math>. [[משתמש:עוזי ו.|עוזי ו.]] 21:30, 9 בפברואר 2012 (IST) | + | '''שאלה'''. בנה שדה מסדר 27. |
| + | |||
| + | '''פתרון'''. הוכחנו שאם f הוא פולינום אי-פריק מעל F, אז חבורת המנה <math>\ K=F[x]/F[x]f(x)</math> היא שדה, שממדו המעלה של f. עלינו למצוא, אם כך, פולינום ממעלה 3 מעל השדה F. לפולינומים מהצורה <math>\ x^3 - a</math> יש שורשים (ולכן אינם פריקים); נבחר את הפולינום <math>\ f(x) = x^3-x+1</math>. עבור הפולינום הזה, K כולל את השאריות של כל הפולינומים מהצורה <math>\ a+bx+cx^2</math> (שמספרם כמובן 27), ופעולת הכפל מקיימת את החוק <math>\ x^3 = x-1</math> (ב-K). | ||
| + | |||
| + | '''שאלה'''. בשדה מסדר 27 הנתון בשאלה הקודמת, מצא בו איבר שסדרו בחבורה הכפלית הוא 13. | ||
| + | |||
| + | '''פתרון'''. החבורה הכפלית של K היא ציקלית מסדר 26 (החבורה הכפלית של כל שדה סופי היא ציקלית). לכן תת-החבורה מסדר 13 היא זו הכוללת את כל הריבועים של אברים ב-K, ובפרט היא נוצרת (כפלית) על-ידי <math>\ x^2</math>. [[משתמש:עוזי ו.|עוזי ו.]] 21:30, 9 בפברואר 2012 (IST) | ||
גרסה מ־18:33, 11 בפברואר 2012
זה המקום לשאול שאלות על דברים שלא היו ברורים משיעורי הבית תנצלו אותו --Matan.Fatal
תרגיל 2
למתי התרגיל? לשבוע הקרוב (שמתחיל ב-13.11) או לזה שאחריו (מתחיל ב-20.11)? נעליים 13:33, 11 בנובמבר 2011 (IST)
- מישהו? נעליים 19:43, 13 בנובמבר 2011 (IST)
לתרגיל מספר 2 קיבלתם שבועיים. --Matan.fatal 21:58, 16 בנובמבר 2011 (IST)
- לתרגיל 2 או לתרגיל 3?
- אלי, מדובר כאן על תרגיל 2 (אבל יש שבועיים גם לתרגיל 3). מתן, תודה על התשובה אבל עד שענית כבר התקיים התרגול שלי השבוע והגשתי את התרגיל. מסתבר גם שהמתרגל בקבוצה שלי (טל) חשב שהתרגיל לשבוע. הבעיה הייתה שבשאלה 16 צריך לדעת מה זה סדר של איבר, דבר שלמדנו רק בשיעור השבוע ולכן הייתי צריך לחפש באינטרנט את ההגדרה. כדי למנוע מצבים כאלה בעתיד אני מבקש לציין על גבי התרגיל את מועד ההגשה (כפי שלשמחתי נעשה בתרגיל 3). נעליים 10:47, 17 בנובמבר 2011 (IST)
שאלה...
אם איבר a הוא מסדר איינסופי, נכון להגיד כי a^n לכל n לא שווה לאפס? ולמה?
תודה
- הכל תלוי למה אתה מחשיב את אפס. האם אתה מחשיב אותו לאיבר הנייטרלי? אם כן, אז התשובה לשאלה שלך היא כן. ההגדרה של סדר של איבר בחבורה הוא ה-n הטבעי המינימלי עבורו a^n=e (כאשר e מסמן איבר נייטרלי). עוד ההגדרה אומרת שהסדר הוא אינסופי אם אין כזה n. מכאן שהתשובה לשאלה שלך פשוט נובעת מההגדרה של סדר של איבר. מקווה שעזרתי, גל.
- קודם כל תשובה מצויינת. שמתי לב ששאלת ועבר הרבה זמן שלא קיבלת תשובה, במידה ואתה שואל שאלה ולא ענו לך עליה תוך יום גג יומיים תשלח מייל לאחד המתרגלים להסתכל. מתן פטאל.
על הבוחן הוירטואלי
בשאלה הראשונה יש 19 סעיפים, שכל אחד מהם נותן מידע נוסף על הנתון הבסיסי (ש-A,B הן תת-חבורות). השאלה היא למצוא את כל הקשרים הלוגיים בין הטענות 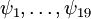 , כלומר, לכל
, כלומר, לכל 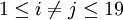 , לקבוע האם הגרירה הלוגית
, לקבוע האם הגרירה הלוגית 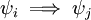 נכונה. אחרי שתזהו כמה טענות שקולות וכמה גרירות טריוויאליות, מספר הבעיות האמיתיות לא יהיה גדול מדי. לצד הוכחת הגרירות התקפות, כדאי שתציגו דוגמאות נגדיות לכל הגרירות שאינן תקפות, אבל חלק זה עשוי להיות קשה יותר.
נכונה. אחרי שתזהו כמה טענות שקולות וכמה גרירות טריוויאליות, מספר הבעיות האמיתיות לא יהיה גדול מדי. לצד הוכחת הגרירות התקפות, כדאי שתציגו דוגמאות נגדיות לכל הגרירות שאינן תקפות, אבל חלק זה עשוי להיות קשה יותר.
אין צורך לחקור קבוצות של טענות (כלומר, גרירות מהסוג 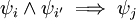 או
או 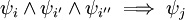 ). עוזי ו. 19:01, 17 בדצמבר 2011 (IST)
). עוזי ו. 19:01, 17 בדצמבר 2011 (IST)
שאלות לקראת הבחינה
- (מתוך מועד ב' תשע"א) "תן דוגמא לתמורה ב-S7 שאין שום דרך להציג כמכפלה של מחזורים באורך 3": בפתרון ניתנה התמורה (2 1) כדוגמא, האם גם תמורת הזהות יכולה להתקבל כתשובה?
- (מתוך מועד ב' תשע"א) "קבע האם החבורות הבאות איזומורפיות או שאינן איזומורפיות":
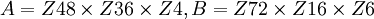 . בפתרון נכתבה ההצגה הקנונית של החבורות:
. בפתרון נכתבה ההצגה הקנונית של החבורות: 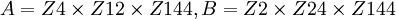 . ברור לי שמכיוון שהאקספוננט של שתי החבורות הוא 144, ההצגה הקנונית של כל אחת מהן תסתיים עם Z144, אך לא ברור לי מדוע בהצגה של A התחלנו עם Z4 ואילו בזו של B עם Z2. נימוק אחר שהוצג בפתרון להיותן לא איזומורפיות היה ש-
. ברור לי שמכיוון שהאקספוננט של שתי החבורות הוא 144, ההצגה הקנונית של כל אחת מהן תסתיים עם Z144, אך לא ברור לי מדוע בהצגה של A התחלנו עם Z4 ואילו בזו של B עם Z2. נימוק אחר שהוצג בפתרון להיותן לא איזומורפיות היה ש-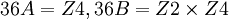 . האם זו דוגמא לשיטה אותה הצגת לקראת סיום ההרצאה ביום חמישי האחרון, בנוגע לקביעת איזומורפיות של חבורות אבליות סופיות, במקום להשתמש במשפט היחידות? האם יש תנאים מגבילים לשימוש בשיטה זו?
. האם זו דוגמא לשיטה אותה הצגת לקראת סיום ההרצאה ביום חמישי האחרון, בנוגע לקביעת איזומורפיות של חבורות אבליות סופיות, במקום להשתמש במשפט היחידות? האם יש תנאים מגבילים לשימוש בשיטה זו? - (מתוך מועד ב' תשע"א) "מיין את החבורות האבליות A מסדר (5^3)*(5^2) כך ש- 4^2 = |4^A/A| ו- 4^3 = |3^A/A|. כתוב את הצורה הקנונית של כל חבורה כזו. כמה חבורות כאלה יש, עד כדי איזומורפיזם?": בפתרון נכתב כי יש לפרק את A למכפלה ישרה פנימית A=BC כאשר 5^2 = |B| ו- 5^3 = |C|. כיצד אנו בטוחים כי ת"ח B,C המוגדרות כך עומדות בתנאים למכפלה ישרה פנימית? במהשך נכתב כי כך נקבל:
 . הבנתי את הדרישה לגבי הסדרים של 3^A ו- 4^A, אך לא הבנתי איך קיבלנו את שני הפירוקים שב- (*).
. הבנתי את הדרישה לגבי הסדרים של 3^A ו- 4^A, אך לא הבנתי איך קיבלנו את שני הפירוקים שב- (*). - (מתוך מועד א' תש"ע) "הוכח שמספר האיברים במחלקת צמידות מחלק את סדר החבורה": הפתרון שלי מעט שונה מזה שתואר בפתרון הבחינה (ומההרצאה). רציתי להראות שכל קוסט של המרכז (centralizer) בחבורה של איבר למעשה מגדיר איבר במחלקת הצמידות, אסמן את המרכז של איבר g כ- (C(g: טענתי שאיבר w שייך לקוסט של (C(g:
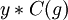 אם"ם w = yx כאשר x איבר ב- (C(g. מכאן ש-
אם"ם w = yx כאשר x איבר ב- (C(g. מכאן ש- 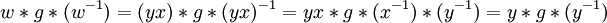 כלומר כל איבר בקוסט
כלומר כל איבר בקוסט 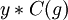 נותן איבר יחיד במחלקת הצמידות של g, ולכן מספר כל הקוסטים של (C(g הוא מספר האיברים במחלקת הצמידות. בכיוון השני טענתי שכל איבר במחלקת הצמידות ניתן לכתיבה כ- (כאשר x איבר ב- (C(g ),
נותן איבר יחיד במחלקת הצמידות של g, ולכן מספר כל הקוסטים של (C(g הוא מספר האיברים במחלקת הצמידות. בכיוון השני טענתי שכל איבר במחלקת הצמידות ניתן לכתיבה כ- (כאשר x איבר ב- (C(g ), 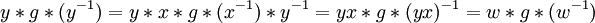 כלומר כל איבר במחלקת הצמידות מגדיר קוסט של (C(g. לכן:
כלומר כל איבר במחלקת הצמידות מגדיר קוסט של (C(g. לכן:![| [g] | = [G:C(g)]](/images/math/8/2/8/8287a5cb40a2bf1abef2a74a82b86241.png) . ומכאן שמספר האיברים במחלקת צמידות מחלק את סדר החבורה. האם הוכחה זו נכונה?
. ומכאן שמספר האיברים במחלקת צמידות מחלק את סדר החבורה. האם הוכחה זו נכונה? - האם יש דרך מובנית למציאת האוטומורפיזמים של חבורה כלשהי (או למי חבורת האוטומורפיזמים שלה איזומורפית)? <מתוך אימייל של סטודנט>
- 1. לא -- תמורת הזהות היא מכפלה של אפס מחזורים באורך 3. אפשר גם להציג אותה כמכפלה של שני מחזורים, בצורה
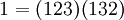 .
. - 2. את ההצגה הקנונית אפשר לחשב על-ידי פירוק פרימרי (פירוק למרכיבים שהם חבורות-p עבור ראשוניים שונים). אפשר "לנחש מראש" את הגורם העליון, הקובע את האקספוננט, אבל את שאר הגורמים צריך לחשב ישירות. ההסבר ל"הופעה" של גורמים אלו או אחרים הוא שזו תוצאת החישוב (באותה מידה קל לנחש ש-347 כפול 491 מתחיל ב-1, אבל אי-אפשר "להסביר" מדוע 7 היא הספרה השניה מימין בלי לבצע את החישוב).
- כדי להוכיח ישירות שהחבורות אינן איזומורפיות, אפשר להשוות תת-חבורות שלהן מהצורה
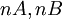 . מכיוון שכפל בקבוע (היינו חיבור חוזר מספר קבוע של פעמים) מתחלף עם איזומורפיזמים, אם שתי החבורות איזומורפיות, גם תת-החבורות מהסוג הזה חייבות להיות איזומורפיות (המגבלה היא אם כן שהחבורות המקוריות תהיינה אבליות, כדי שכפל בקבוע יהיה הומומורפיזם).
. מכיוון שכפל בקבוע (היינו חיבור חוזר מספר קבוע של פעמים) מתחלף עם איזומורפיזמים, אם שתי החבורות איזומורפיות, גם תת-החבורות מהסוג הזה חייבות להיות איזומורפיות (המגבלה היא אם כן שהחבורות המקוריות תהיינה אבליות, כדי שכפל בקבוע יהיה הומומורפיזם).
- כדי להוכיח ישירות שהחבורות אינן איזומורפיות, אפשר להשוות תת-חבורות שלהן מהצורה
- 3. אם A חבורה מסדר nm כאשר n,m זרים, ו-
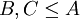 תת-חבורות מסדרים n,m בהתאמה, אז הן מוכרחות להיות זרות (לכל איבר משותף יש סדר המחלק גם את n וגם את m), ולכן גם
תת-חבורות מסדרים n,m בהתאמה, אז הן מוכרחות להיות זרות (לכל איבר משותף יש סדר המחלק גם את n וגם את m), ולכן גם 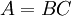 (משום שכאשר BC תת-חבורה של חבורה כלשהי, מתקיים
(משום שכאשר BC תת-חבורה של חבורה כלשהי, מתקיים 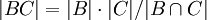 ). כעת, אם
). כעת, אם 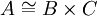 , אז
, אז 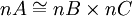 , ומכאן הפירוקים שב-(*).
, ומכאן הפירוקים שב-(*). - 4. ההוכחה הזו דומה לזו שנתנו בכתה: הרעיון הוא לבנות התאמה בין קוסטים של המרכז לבין אברים במחלקת הצמידות.
- 5. אלגוריתמית, בהנתן לוח הכפל של החבורה - בוודאי: אפשר לעבור על כל התמורות האפשריות, ולבחון אלו מהן שומרות על הפעולה. בפועל השיטה הזו אינה מעשית, וכדי למצוא את *כל* האוטומורפיזמים צריך להכיר את מבנה החבורה, למשל דרך "צורה נורמלית" (כלומר צורה מוגדרת היטב שאליה אפשר להביא כל איבר בחבורה, באופן כזה ששני אברים עם צורה נורמלית שונה מוכרחים להיות שונים), ואז לפתור את המשוואות שהיחסים שלה מגדירים. התשובה הקצרה היא: לא. עוזי ו. 11:34, 8 בפברואר 2012 (IST)
- 1. לא -- תמורת הזהות היא מכפלה של אפס מחזורים באורך 3. אפשר גם להציג אותה כמכפלה של שני מחזורים, בצורה
בניית שדה מסדר 27
שאלה. הוכח שקיים שדה מסדר 27.
פתרון. נתבונן בפולינום 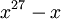 מעל השדה
מעל השדה 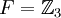 . הוכחנו שיש שדה המפצל את הפולינום הזה, ובתוך אותו שדה, אוסף השורשים של הפולינום סגור לחיבור וכפל, ולכן הוא מהווה שדה מסדר 27.
. הוכחנו שיש שדה המפצל את הפולינום הזה, ובתוך אותו שדה, אוסף השורשים של הפולינום סגור לחיבור וכפל, ולכן הוא מהווה שדה מסדר 27.
שאלה. בנה שדה מסדר 27.
פתרון. הוכחנו שאם f הוא פולינום אי-פריק מעל F, אז חבורת המנה ![\ K=F[x]/F[x]f(x)](/images/math/4/8/e/48ea5b08216e96fa6f28d36ff0edddd4.png) היא שדה, שממדו המעלה של f. עלינו למצוא, אם כך, פולינום ממעלה 3 מעל השדה F. לפולינומים מהצורה
היא שדה, שממדו המעלה של f. עלינו למצוא, אם כך, פולינום ממעלה 3 מעל השדה F. לפולינומים מהצורה 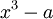 יש שורשים (ולכן אינם פריקים); נבחר את הפולינום
יש שורשים (ולכן אינם פריקים); נבחר את הפולינום 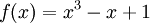 . עבור הפולינום הזה, K כולל את השאריות של כל הפולינומים מהצורה
. עבור הפולינום הזה, K כולל את השאריות של כל הפולינומים מהצורה 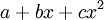 (שמספרם כמובן 27), ופעולת הכפל מקיימת את החוק
(שמספרם כמובן 27), ופעולת הכפל מקיימת את החוק 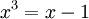 (ב-K).
(ב-K).
שאלה. בשדה מסדר 27 הנתון בשאלה הקודמת, מצא בו איבר שסדרו בחבורה הכפלית הוא 13.
פתרון. החבורה הכפלית של K היא ציקלית מסדר 26 (החבורה הכפלית של כל שדה סופי היא ציקלית). לכן תת-החבורה מסדר 13 היא זו הכוללת את כל הריבועים של אברים ב-K, ובפרט היא נוצרת (כפלית) על-ידי 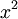 . עוזי ו. 21:30, 9 בפברואר 2012 (IST)
. עוזי ו. 21:30, 9 בפברואר 2012 (IST)