שיחה:89-214 סמסטר א' תשעד
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
שאלה 3 בתרגיל בית 1
נניח אני רוצה לבטא את המחלק המשותף המקסימלי של 840,575 כצירוף לינארי שלהם.
בשלב הראשון, אני מוצא את המחלק המשותף המקסימלי ע"י אלגוריתם אוקלידיס באופן הבא:
zz (840,575)=(575,265)=(265,45)=(45,40)=(40,5)=5 zz
המעבר הראשון משמאל לימין, נובע מכך ש: zz 840=575*1+265 zz
המעבר השני משמאל לימין, נובע מכך ש: zz 575=265*2+45 zz
המעבר השלישי משמאל לימין נובע מכך ש: zz 265=45*5+40 zz
המעבר הרביעי משמאל לימין נובע מכך ש: zz 45=40*1+5 zz
המעבר האחרון נובע מכך שהמחלק המשותף המקסימלי של 40 ו-5 הוא 5.
כעת מה שאני רוצה לעשות, זה לבטא את המחלק המשותף המקסימלי של 840,575 שהוא כאמור המספר 5, כצירוף לינארי של 840, 575. כיצד בדיוק אני עושה את זה. ראיתי פתרון בתרגול, אבל השיטה לא ממש מובנת לי. אשמח להסבר מפורט, כיצד בדיוק אני צריך לעשות את זה.
תודה מראש ושבת שלום!
- שתי הערות עריכה בויקי: כדאי להשתמש בכותרות (מוסיפים עם מספר של "=" משני הצדדים) וכדאי להשתמש בכתיב מתמטי (הכפתור עם
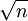 ) כדי להכניס ביטויים מתמטיים.
) כדי להכניס ביטויים מתמטיים. - התשובה לשאלה היא פשוט ליישם את אלגוריתם אוקלידס המורחב. רמז קל: זה גם מה שנדרש בשאלה 1. בקישור יש כמה דוגמאות מפורטות.
- הדרך שבה מצאת את המחלק המשותף המקסימלי נכונה, ודרושה להמשך. בכל שלב (מעבר) באלגוריתם אוקלידס אפשר להציג את שארית החלוקה
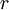 כצירוף של שני המספרים שמחלקים
כצירוף של שני המספרים שמחלקים 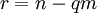 . נתחיל מן השלב האחרון ונתקדם "מעלה":
. נתחיל מן השלב האחרון ונתקדם "מעלה":
- בסוף קיבלת כי
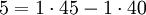 .
. - נציב את הביטוי ל-
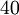 מהשלב אחד לפני האחרון
מהשלב אחד לפני האחרון 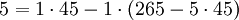 . אם נצמצם נקבל
. אם נצמצם נקבל 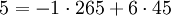 .
. - כעת מציבים ביטוי עבור
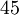 עם
עם 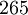 ו-
ו-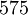 .
.
- בסוף קיבלת כי
- כך ממשיכים עד שמגיעים לביטוי עם המספרים המקוריים שעבורם חיפשנו
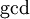 .
.
אם f | 2c וגם f | 2d האם אני יכול להסיק מכך ש- ( f | (2c,2d ?
תודה.
- כרמז, מה יקרה אם פשוט נסמן
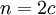 וגם
וגם 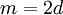 ? מה יודעים אם
? מה יודעים אם 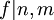 ?
? - מה שיודעים, זה ש-f מחלק כל צירוף לינארי של n ושל m? איך אני יכול להסיק מזה ש-f מחלק את (n,m) ?
- לזה בדיוק התכוונתי. לגב מה שאתה מנסה להסיק: ראינו בכיתה תכונה חשובה של ה-
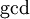 . איך אפשר להציג אותו?
. איך אפשר להציג אותו?
- לזה בדיוק התכוונתי. לגב מה שאתה מנסה להסיק: ראינו בכיתה תכונה חשובה של ה-
שאלה 4 סעיף ג'
שתיי שאלות:
1. האם אני יכול לומר שקיים מספר x כך ש- x|a+b וגם x|a-b? אם כן, למה?
2. במידה ואני יכול לטעון את מה שכתבתי בשאלה 1, ובמידה והראיתי ש- x|2d, האם אני יכול לומר ש- zz (a+b,a-b) | 2d zz ? אם כן, למה?
- הערת עריכה בויקי: אפשר לייצר רשימה ממוספרת על ידי שימוש בסולמית (#) בתחילת השורה.
- לא לגמרי הבנתי את השאלה: לכל זוג מספרים הגדרנו את הממ"מ, ובכל מקרה
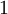 תמיד מחלק כל מספר. בגלל זה, אפשר להתחיל את הפתרון עם הנחה כמו "יהי
תמיד מחלק כל מספר. בגלל זה, אפשר להתחיל את הפתרון עם הנחה כמו "יהי 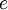 מחלק משותף (לאו דווקא מקסימלי) של
מחלק משותף (לאו דווקא מקסימלי) של 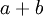 ושל
ושל 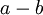 ..."
..." - הרמז הוא שאפשר להשתמש בשאלה 4 סעיף ב' כדי לפתור את הסעיף הנוכחי. מה אתה יודע על הסכום וההפרש של
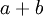 ושל
ושל 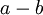 ?
?
- לא לגמרי הבנתי את השאלה: לכל זוג מספרים הגדרנו את הממ"מ, ובכל מקרה
מה שאני יודע שזה ש-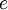 מחלק גם את הסכום שלהם וגם את ההפרש שלהם. כלומר את
מחלק גם את הסכום שלהם וגם את ההפרש שלהם. כלומר את 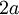 ואת
ואת 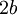 .
.
- מצוין! מה זה אומר שמתקיים
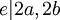 ? את מה עוד
? את מה עוד 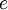 מחלק?
מחלק?
שאלה
אם p מספר ראשוני, שלא מחלק את המספר a, למה נובע מכך ש- 1=(a,p) ? למעשה על מנת להגיד שהמחלק המשותף המקסימלי של a ו-p הוא 1, אני צריך לדעת גם ש-p לא מחלק את a, אבל גם ש-a לא מחלק את p. a לא מחלק את p מהסיבה ש-p ראשוני, ולכן בסה"כ a לא מחלק את P , ו-p לא מחלק את a ולכן המחלק המשותף המקסימלי הוא 1?
זה ההסבר?
- יש כאן קצת סלט. קודם כל, רקע: עבור כל
 מתקיים
מתקיים 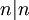 וכמו כן
וכמו כן 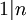 . כאשר אנחנו מחפשים
. כאשר אנחנו מחפשים 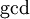 צריך למצוא את המספר הטבעי הגדול ביותר שמחלק גם את
צריך למצוא את המספר הטבעי הגדול ביותר שמחלק גם את 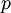 וגם את
וגם את 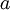 . המספרים הטבעיים היחידים שמחלקים את
. המספרים הטבעיים היחידים שמחלקים את 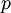 הם כידוע רק
הם כידוע רק 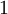 ו-
ו-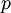 . נתון כי
. נתון כי 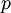 לא מחלק את
לא מחלק את 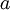 , כלומר הוא לא מקיים את התנאי שנדרש להיות
, כלומר הוא לא מקיים את התנאי שנדרש להיות 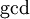 שדורש לחלק את
שדורש לחלק את 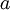 . לכן נקבל
. לכן נקבל 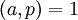 .
.
שאלה 6 בתרגיל 1
מה הכוונה למצוא מס' שלם חיובי  כך ש-
כך ש-
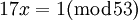
לא ברור לי מה הכוונה ומה המשמעות של ה-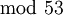 הזה..
הזה..
- נא להשתמש בכפתור לנוסחאות מתמטיות. המשמעות של
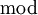 הוא לומר כי מדובר במשוואה מודולו
הוא לומר כי מדובר במשוואה מודולו 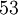 . כלומר מבקשים למצוא מספר
. כלומר מבקשים למצוא מספר  כך שאם תכפול אותו ב-
כך שאם תכפול אותו ב-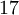 תקבל מספר שבחלוקה ב-
תקבל מספר שבחלוקה ב-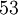 תקבל שארית
תקבל שארית 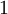 .
.