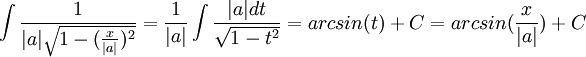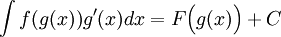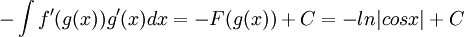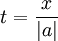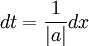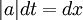שיטת ההצבה
מתוך Math-Wiki
גרסה מ־09:29, 18 במרץ 2012 מאת ארז שיינר (שיחה | תרומות) (יצירת דף עם התוכן "==הגדרה== שיטת ההצבה היא שיטת החלפת משתנים לצורך אינטגרציה, לפי כלל השרשרת לגזירה. <math>[f(g(x))]'...")
הגדרה
שיטת ההצבה היא שיטת החלפת משתנים לצורך אינטגרציה, לפי כלל השרשרת לגזירה.
![[f(g(x))]'=f'(g(x))g'(x)](/images/math/6/3/9/639e2d8d7ed8b111e67f6a8dadd0f0fe.png)
לכן, נוסחאת ההצבה הינה:
כאשר 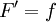
סימון נוח יותר לאותה הנוסחא:
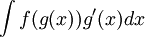
נסמן 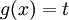
ולכן 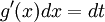
ולכן 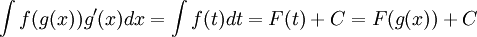
הסימון הזה נוח יותר לפתרון תרגילים מאשר הסימון הראשון שנובע ישירות מכלל השרשרת.
דוגמאות
א.
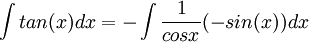
נסמן 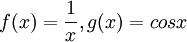
לכן 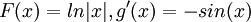 וסה"כ האינטגרל הוא מהצורה:
וסה"כ האינטגרל הוא מהצורה:
ב.
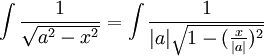
נציב
לכן
לכן
ולכן