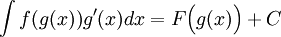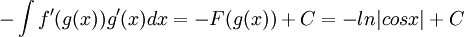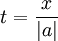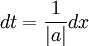שיטת ההצבה
מתוך Math-Wiki
שיטת ההצבה
שיטת ההצבה היא שיטת החלפת משתנים לצורך אינטגרציה, לפי כלל השרשרת לגזירה.
![[f(g(x))]'=f'(g(x))g'(x)](/images/math/6/3/9/639e2d8d7ed8b111e67f6a8dadd0f0fe.png)
לכן, נוסחאת ההצבה הינה:
כאשר 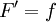
סימון נוח יותר לאותה הנוסחא:
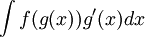
נסמן 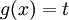
ולכן 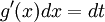
ולכן 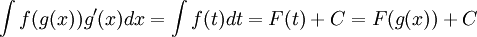
הסימון הזה נוח יותר לפתרון תרגילים מאשר הסימון הראשון שנובע ישירות מכלל השרשרת.
אלגוריתם לביצוע הצבה
נתאר כעת את השלבים בביצוע הצבה, במקרים שונים.
- בוחרים הצבה
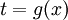 או
או 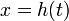
- גוזרים את שני הצדדים וכופלים ב
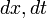 .
.
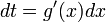 או
או 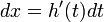
- במקרה הראשון, אם הביטוי
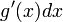 אינו מופיע באינטגרל, והפונקציה g הפיכה, נחליף להצבה
אינו מופיע באינטגרל, והפונקציה g הפיכה, נחליף להצבה 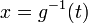
- כמו כן, אם לאחר ההצבה נותרו מופעים של המשתנה x, נוכל להשלים את ההצבה רק אם g הפיכה ע"י
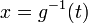
דוגמאות
א.
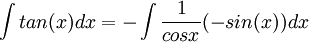
נסמן 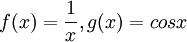
לכן 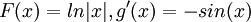 וסה"כ האינטגרל הוא מהצורה:
וסה"כ האינטגרל הוא מהצורה:
ב.
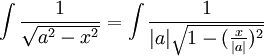
נציב
לכן
לכן
ולכן
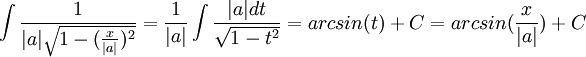
הצבות אוניברסאליות
הצבות אוניברסאליות הוא כינוי כללי להצבות המעבירות פונקציות ממשפחה מסויימת לצורה של פונקציה רציונאלית אותה אנחנו יודעים לפתור. שימו לב שכיוון ופתרון פונקציה רציונאלית דורש פירוק פולינומים, לעיתים המעבר לפונקציה רציונאלית לא יקדם אותנו לקראת פתרון הבעייה.
הצבות אוניברסאליות ידועות ניתן למצוא בקובץ הבא: (עד אשר מישהו יקליד אותו אל תוך הויקי...)