הבדלים בין גרסאות בדף "תרגול 4 תשעז"
(יצירת דף עם התוכן "=רעיון בסיסי - אינדוקציה על הטבעיים= בשביל להוכיח שטענה מסוימת <math>P(n)</math> נכונה עבור כל מ...") |
(←הכללה פשוטה שנייה) |
||
| (7 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | + | חזרה ל[[83-116, בדידה 1 להנדסה, מערכי תרגול|דף מערכי התרגול]]. | |
| − | + | =אינדוקציה מתמטית: רעיון בסיסי= | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | אינדוקציה היא שיטה המאפשרת להוכיח שטענה מסוימת <math>P(n)</math> נכונה עבור כל מספר טבעי | |
| − | + | (למשל <math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math>) בעזרת הסקה מן הפרט אל הכלל. | |
| − | + | הוכחת הטענה <math>\forall nP(n)</math> שקולה להוכחת שתי הטענות הבאות: | |
| + | * (בסיס האינדוקציה) הטענה מתקיימת עבור <math>n=1</math>. כלומר <math>P(1)</math> נכון. | ||
| + | * (צעד האינדוקציה) '''אם''' הטענה נכונה עבור מספר טבעי מסוים, אז היא נכונה גם עבור המספר הבא אחריו. כלומר <math>P(n)\rightarrow P(n+1)</math>. | ||
| + | |||
| + | למה זה מספיק? בוא נחשוב. הוכחנו באופן ישיר כי הטענה נכונה עבור <math>n=1</math> כלומר <math>P(1)</math> מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור <math>n=1</math> (שזה אכן כך) אז הטענה נכונה גם עבור <math>n=2</math>. כלומר <math>P(2)</math>. אה! אז עכשיו זה נכון עבור <math>n=2</math>, אז לפי אותה טענה זה נכון גם עבור <math>n=3</math>! ומה עכשיו? אם זה נכון עבור <math>n=3</math>, זה נכון עבור <math>n=4</math>. וכן הלאה באותה הדרך. אפשר להשתכנע שבסופו של דבר <math>P(n)</math> נכון '''לכל''' <math>n</math>. | ||
| + | |||
| + | '''דוגמה:''' | ||
נוכיח באינדוקציה כי הטענה <math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math> | נוכיח באינדוקציה כי הטענה <math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math> | ||
| − | נכונה לכל <math>n\in \mathbb{N} </math> טבעי | + | נכונה לכל <math>n\in \mathbb{N} </math> טבעי. |
הוכחה: | הוכחה: | ||
| − | עבור <math>n=1</math> אכן מתקיים כי <math>1^2=1^3</math> | + | עבור <math>n=1</math> אכן מתקיים כי <math>1^2=1^3</math>. |
כעת נראה שאם הטענה נכונה עבור <math>n</math> כלשהוא, כלומר אם מתקיים | כעת נראה שאם הטענה נכונה עבור <math>n</math> כלשהוא, כלומר אם מתקיים | ||
| שורה 25: | שורה 28: | ||
<math>(1+2+\cdots +n+(n+1))^2=(1+2+\cdots +n)^2+2\cdot(1+2+\cdots +n)(n+1)+(n+1)^2 </math> | <math>(1+2+\cdots +n+(n+1))^2=(1+2+\cdots +n)^2+2\cdot(1+2+\cdots +n)(n+1)+(n+1)^2 </math> | ||
| − | לפי הנחת האינדוקציה אפשר להמשיך הלאה | + | לפי הנחת האינדוקציה אפשר להמשיך הלאה: |
<math>=1^3 +2^3 + \cdots +n^3 +2\cdot (1+2+\cdots +n)(n+1)+(n+1)^2 </math> | <math>=1^3 +2^3 + \cdots +n^3 +2\cdot (1+2+\cdots +n)(n+1)+(n+1)^2 </math> | ||
| שורה 32: | שורה 35: | ||
<math>=1^3 +2^3 + \cdots +n^3 +(1+n)(n+1)^2=1^3 +2^3 + \cdots +n^3+(n+1)^3</math> | <math>=1^3 +2^3 + \cdots +n^3 +(1+n)(n+1)^2=1^3 +2^3 + \cdots +n^3+(n+1)^3</math> | ||
| − | וסיימנו | + | וסיימנו. |
| − | + | ||
| − | + | '''דוגמה:''' | |
הוכח כי לכל מספר טבעי <math>n</math> מתקיים כי <math>2+4+6+\cdots +2n=n(n+1)</math> | הוכח כי לכל מספר טבעי <math>n</math> מתקיים כי <math>2+4+6+\cdots +2n=n(n+1)</math> | ||
| שורה 53: | שורה 55: | ||
שזה הטענה עבור <math>n+1</math> וסיימנו. | שזה הטענה עבור <math>n+1</math> וסיימנו. | ||
| − | + | =הכללות= | |
| − | + | ==הכללה פשוטה ראשונה== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | הכללה ישירה שבה יש שינוי רק בבסיס האינדוקציה: אם נוכיח עבור טענה <math>P(n)</math> כי: | |
| + | * הטענה מתקיימת עבור <math>n=k</math> מסוים. כלומר <math>P(k)</math> נכונה. | ||
| + | * '''אם''' הטענה נכונה עבור מספר טבעי מסוים, אז היא נכונה גם עבור המספר הבא אחריו. כלומר <math>P(n)\rightarrow P(n+1)</math>. | ||
| − | + | אז באופן דומה הטענה נכונה <math>P(n)</math> נכונה עבור <math>n\geq k</math>. | |
| + | כלומר - במקום להוכיח עבור <math>n=1</math> ואז הטענה מתקיימת החל מ-<math>1</math> ניתן להוכיח עבור <math>n=k</math> ואז הטענה מתקיים החל מ-<math>k</math>. | ||
| − | + | '''דוגמה:''' | |
| − | + | הוכח כי לכל <math>x>0</math> מתקיים <math>(1+x)^n > 1+nx</math> לכל <math>n\geq 2</math>. | |
| − | הוכח כי לכל <math>x>0</math> מתקיים <math>(1+x)^n > 1+nx</math> לכל <math>n\geq 2</math> | + | |
פתרון: | פתרון: | ||
| − | עבור <math>n=2</math> נקבל <math>(1+x)^2 = 1+2x+x^2>1+2x</math> כי <math>x>0</math> | + | עבור <math>n=2</math> נקבל <math>(1+x)^2 = 1+2x+x^2>1+2x</math> כי <math>x>0</math> . |
| − | כעת נניח כי הטענה נכונה עבור <math>n</math> | + | כעת נניח כי הטענה נכונה עבור <math>n</math> כלשהו, כלומר מתקיים <math>(1+x)^n > 1+nx</math>. |
נוכיח עבור <math>n+1</math> מהנחת האינדוקציה נקבל כי | נוכיח עבור <math>n+1</math> מהנחת האינדוקציה נקבל כי | ||
| − | <math> (1+x)^{n+1}=(1+x)^n\cdot (1+x)>(1+nx) (1+x)= | + | <math>(1+x)^{n+1}=(1+x)^n\cdot (1+x)>(1+nx) (1+x)</math> |
| + | <math>=1+nx +x+nx^2 > 1+x+nx =1+ (n+1)x</math> | ||
| + | |||
| + | וסיימנו. | ||
| − | + | ==הכללה פשוטה שנייה== | |
| − | + | הכללה שבה יש שינוי בצעד האינדוקציה, הנקראת אינדוקציה שלמה: אם נוכיח עבור טענה <math>P(n)</math> כי: | |
| − | אם נוכיח עבור טענה <math>P(n)</math> | + | * הטענה מתקיימת עבור <math>n=1</math>. כלומר <math>P(1)</math> נכונה. |
| − | * הטענה מתקיימת עבור <math>n=1</math> | + | |
* '''אם''' הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים <math>n</math> (כלומר מתקיים <math>P(m)</math> עבור <math>m\leq n</math>) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר <math>P(n+1)</math> מתקיים). | * '''אם''' הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים <math>n</math> (כלומר מתקיים <math>P(m)</math> עבור <math>m\leq n</math>) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר <math>P(n+1)</math> מתקיים). | ||
| − | אז באופן דומה הטענה נכונה <math>P(n)</math> נכונה עבור <math>n\geq 1</math> | + | אז באופן דומה הטענה נכונה <math>P(n)</math> נכונה עבור <math>n\geq 1</math>. |
כלומר - אפשר להחליף את ההנחה שמתקיים עבור <math>n</math> ולהוכיח עבור <math>n+1</math> | כלומר - אפשר להחליף את ההנחה שמתקיים עבור <math>n</math> ולהוכיח עבור <math>n+1</math> | ||
| − | בהנחה שמתקיים עבור כל מי ש'''קטן שווה''' <math>n</math> ולהוכיח עבור <math>n+1</math> | + | בהנחה שמתקיים עבור כל מי ש'''קטן שווה''' <math>n</math> ולהוכיח עבור <math>n+1</math>. |
| − | + | ====תרגיל (בד"כ נעשה בהרצאה)==== | |
| − | + | כל מספר טבעי <math>1<n </math> ניתן להציגו כמכפלה של מספרים ראשוניים. | |
| − | כל מספר טבעי <math>1<n </math> ניתן להציגו כמכפלה של מספרים ראשוניים | + | |
הוכחה: | הוכחה: | ||
| שורה 97: | שורה 99: | ||
עבור <math>n=2</math> זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו. | עבור <math>n=2</math> זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו. | ||
| − | כעת נניח שהטענה נכונה לכל <math>1<k\leq n</math> ונוכיח עבור <math>n+1</math> | + | כעת נניח שהטענה נכונה לכל <math>1<k\leq n</math> ונוכיח עבור <math>n+1</math>. |
אם <math>n+1</math> ראשוני - סיימנו כי אז הוא הפירוק של עצמו. | אם <math>n+1</math> ראשוני - סיימנו כי אז הוא הפירוק של עצמו. | ||
| שורה 103: | שורה 105: | ||
אחרת <math>n+1</math> מתפרק למכפלה <math>n+1=ab</math> כאשר <math>1<a,b<n+1</math> | אחרת <math>n+1</math> מתפרק למכפלה <math>n+1=ab</math> כאשר <math>1<a,b<n+1</math> | ||
לפי הנחת האינדוקציה <math>a,b</math> מתפרקים למכפלה של מספרים ראשוניים | לפי הנחת האינדוקציה <math>a,b</math> מתפרקים למכפלה של מספרים ראשוניים | ||
| − | <math>a=\ | + | <math>a=\prod_{k=1}^l p_k,b=\prod_{i=1}^r q_i</math> כאשר <math>p_k,q_i</math> ראשוניים. |
| − | + | אזי <math>n+1=ab=\prod_{k=1}^l p_k\cdot \prod_{i=1}^r q_i</math> וסיימנו. | |
| − | + | ====תרגיל==== | |
| + | שאלת השוקולוד. | ||
| − | + | =תרגילים יותר מעניינים= | |
| − | + | ==תרגיל == | |
יהא <math>A</math> פסוק. נגדיר בעזרת אינדוקציה פסוקים: | יהא <math>A</math> פסוק. נגדיר בעזרת אינדוקציה פסוקים: | ||
<math>P_0 = A, P_n=(P_{n-1})\to A</math> | <math>P_0 = A, P_n=(P_{n-1})\to A</math> | ||
| − | |||
| − | |||
| − | + | הוכיחו כי <math>P_{n}</math> טאוטולוגיה כאשר <math>n</math> אי-זוגי. | |
| − | + | ||
| + | פתרון: | ||
| + | נוכיח באינדוקציה כי לכל <math>n</math> אי-זוגי, הפסוק <math>P_{n}</math> | ||
| + | הוא טאוטולוגיה. בדיקה: עבור <math>n=1</math>, הפסוק הוא <math>A\to A</math>. הוא אכן טאוטולוגיה. | ||
צעד: כעת, נניח את נכונות הטענה עבור <math>n</math> אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר <math>n+2</math>. | צעד: כעת, נניח את נכונות הטענה עבור <math>n</math> אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר <math>n+2</math>. | ||
| − | מתקיים:<math>P_{n+2}=P_{n+1}\to A=(P_{n}\to A)\to A</math> נראה כי זו אכן | + | מתקיים:<math>P_{n+2}=P_{n+1}\to A=(P_{n}\to A)\to A</math> נראה כי זו אכן טאוטולוגיה. ראשית, לפי ההנחה, <math>P_{n}\equiv T</math> |
לכל ערך של <math>A</math>. | לכל ערך של <math>A</math>. | ||
| − | + | * אם <math>A=F</math>, נקבל <math>(T\to F)\to F\equiv F\to F</math>- אכן אמת. | |
| − | + | * אם <math>A=T</math>, נקבל <math> (T\to T)\to T\equiv T\to T</math> - אכן אמת. | |
וסיימנו באינדוקציה. | וסיימנו באינדוקציה. | ||
| − | + | ==תרגיל== | |
| − | יהיו <math>A_1,A_2\dots A_{m+1} \in \mathbb{F}^{n\times n}</math> מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י | + | יהיו <math>A_1,A_2\dots A_{m+1} \in \mathbb{F}^{n\times n}</math> מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחה |
<math>(A_1A_2\cdots A_{m+1})_{i,j}=\underset{1\leq i_1,i_2,\dots i_m \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,j}</math> | <math>(A_1A_2\cdots A_{m+1})_{i,j}=\underset{1\leq i_1,i_2,\dots i_m \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,j}</math> | ||
הוכחה (באינדוקציה על מספר המטריצות): | הוכחה (באינדוקציה על מספר המטריצות): | ||
| − | עבור <math>m=1</math> זה ההגדרה של כפל בין 2 מטריצות | + | עבור <math>m=1</math> זה ההגדרה של כפל בין 2 מטריצות. |
| − | כעת, נניח שהטענה נכונה עבור <math>m</math> | + | כעת, נניח שהטענה נכונה עבור <math>m</math> כלשהו. נוכיח נכונות עבור <math>m+1</math>. |
<math>(A_1A_2\cdots A_{m+1}A_{m+2})_{i,j}=\sum_{i_{m+1}=1}^n (A_1A_2\cdots A_{m+1})_{i,i_{m+1}}(A_{m+2})_{i_{m+1},j}</math> | <math>(A_1A_2\cdots A_{m+1}A_{m+2})_{i,j}=\sum_{i_{m+1}=1}^n (A_1A_2\cdots A_{m+1})_{i,i_{m+1}}(A_{m+2})_{i_{m+1},j}</math> | ||
| שורה 153: | שורה 156: | ||
==אזהרה== | ==אזהרה== | ||
| − | אינדוקציה היא כלי חזק אך יש לשים לב כי משתמשים בו | + | אינדוקציה היא כלי חזק אך יש לשים לב כי משתמשים בו נכון. |
| − | + | דוגמה מפורסמת להוכחת שגויה באינדוקציה היא הדוגמה הבאה: | |
טענה: כל קבוצה של סוסים לא ריקה מכילה סוסים מצבע יחיד. | טענה: כל קבוצה של סוסים לא ריקה מכילה סוסים מצבע יחיד. | ||
| שורה 161: | שורה 164: | ||
"הוכחה": נוכיח בעזרת אינדוקציה על מספר האיברים בקבוצת הסוסים. | "הוכחה": נוכיח בעזרת אינדוקציה על מספר האיברים בקבוצת הסוסים. | ||
| − | עבור <math>n=1</math> אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד | + | עבור <math>n=1</math> אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד. |
| − | כעת נניח כל קבוצה עם <math>n</math> סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל <math>n+1</math> | + | כעת נניח כל קבוצה עם <math>n</math> סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל <math>n+1</math>. |
תהא <math>H=\{h_1,h_2,\dots h_n,h_{n+1}\}</math> קבוצה עם <math>n+1</math> סוסים אזי לפי הנחת האינדוקציה | תהא <math>H=\{h_1,h_2,\dots h_n,h_{n+1}\}</math> קבוצה עם <math>n+1</math> סוסים אזי לפי הנחת האינדוקציה | ||
| − | <math>H_1 =\{h_1,h_2,\dots h_n\}</math> ו <math>H_2=\{h_2,\dots h_n,h_{n+1}\}</math> הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל <math>n</math>) | + | <math>H_1 =\{h_1,h_2,\dots h_n\}</math> ו-<math>H_2=\{h_2,\dots h_n,h_{n+1}\}</math> הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל <math>n</math>), |
| − | ולכן כל הסוסים ב <math>H</math> | + | ולכן כל הסוסים ב-<math>H</math> גם כן בעלי צבע יחיד (כי יש חפיפה בין <math>H_1</math> ובין <math>H_2</math>). |
| − | + | ||
| − | חישבו איפה השגיאה (רמז: במעבר מ <math>n=1</math> ל <math>n=2</math>) | + | חישבו איפה השגיאה (רמז: במעבר מ <math>n=1</math> ל <math>n=2</math>). |
גרסה אחרונה מ־12:12, 8 בדצמבר 2019
חזרה לדף מערכי התרגול.
תוכן עניינים
אינדוקציה מתמטית: רעיון בסיסי
אינדוקציה היא שיטה המאפשרת להוכיח שטענה מסוימת 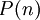 נכונה עבור כל מספר טבעי
(למשל
נכונה עבור כל מספר טבעי
(למשל 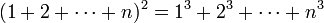 ) בעזרת הסקה מן הפרט אל הכלל.
) בעזרת הסקה מן הפרט אל הכלל.
הוכחת הטענה 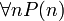 שקולה להוכחת שתי הטענות הבאות:
שקולה להוכחת שתי הטענות הבאות:
- (בסיס האינדוקציה) הטענה מתקיימת עבור
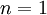 . כלומר
. כלומר 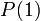 נכון.
נכון. - (צעד האינדוקציה) אם הטענה נכונה עבור מספר טבעי מסוים, אז היא נכונה גם עבור המספר הבא אחריו. כלומר
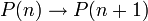 .
.
למה זה מספיק? בוא נחשוב. הוכחנו באופן ישיר כי הטענה נכונה עבור 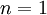 כלומר
כלומר 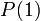 מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור
מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור 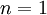 (שזה אכן כך) אז הטענה נכונה גם עבור
(שזה אכן כך) אז הטענה נכונה גם עבור 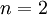 . כלומר
. כלומר 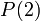 . אה! אז עכשיו זה נכון עבור
. אה! אז עכשיו זה נכון עבור 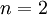 , אז לפי אותה טענה זה נכון גם עבור
, אז לפי אותה טענה זה נכון גם עבור 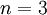 ! ומה עכשיו? אם זה נכון עבור
! ומה עכשיו? אם זה נכון עבור 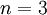 , זה נכון עבור
, זה נכון עבור 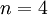 . וכן הלאה באותה הדרך. אפשר להשתכנע שבסופו של דבר
. וכן הלאה באותה הדרך. אפשר להשתכנע שבסופו של דבר 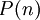 נכון לכל
נכון לכל  .
.
דוגמה:
נוכיח באינדוקציה כי הטענה 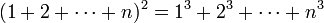 נכונה לכל
נכונה לכל 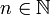 טבעי.
טבעי.
הוכחה:
עבור 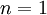 אכן מתקיים כי
אכן מתקיים כי 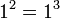 .
.
כעת נראה שאם הטענה נכונה עבור  כלשהוא, כלומר אם מתקיים
כלשהוא, כלומר אם מתקיים
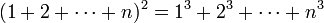 אזי הטענה נכונה עבור
אזי הטענה נכונה עבור 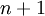 , כלומר
, כלומר
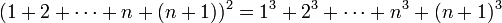 . כלומר נוכיח ש:
. כלומר נוכיח ש: 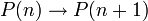
נוכיח:
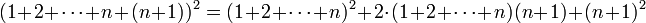
לפי הנחת האינדוקציה אפשר להמשיך הלאה:
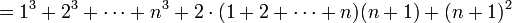
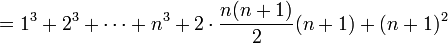
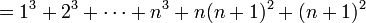
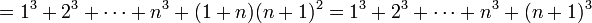
וסיימנו.
דוגמה:
הוכח כי לכל מספר טבעי  מתקיים כי
מתקיים כי 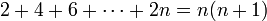
פתרון:
עבור 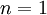 אכן מתקיים
אכן מתקיים 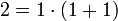
כעת נניח שהטענה נכונה עבור  ונוכיח את הטענה עבור
ונוכיח את הטענה עבור 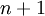
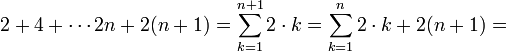
לפי הנחת האינדוקציה ניתן להמשיך
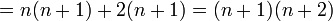
שזה הטענה עבור 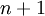 וסיימנו.
וסיימנו.
הכללות
הכללה פשוטה ראשונה
הכללה ישירה שבה יש שינוי רק בבסיס האינדוקציה: אם נוכיח עבור טענה 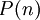 כי:
כי:
- הטענה מתקיימת עבור
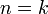 מסוים. כלומר
מסוים. כלומר 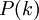 נכונה.
נכונה. - אם הטענה נכונה עבור מספר טבעי מסוים, אז היא נכונה גם עבור המספר הבא אחריו. כלומר
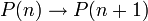 .
.
אז באופן דומה הטענה נכונה 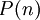 נכונה עבור
נכונה עבור 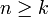 .
.
כלומר - במקום להוכיח עבור 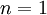 ואז הטענה מתקיימת החל מ-
ואז הטענה מתקיימת החל מ-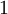 ניתן להוכיח עבור
ניתן להוכיח עבור 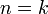 ואז הטענה מתקיים החל מ-
ואז הטענה מתקיים החל מ-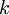 .
.
דוגמה:
הוכח כי לכל 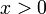 מתקיים
מתקיים 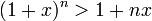 לכל
לכל 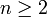 .
.
פתרון:
עבור 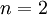 נקבל
נקבל  כי
כי 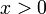 .
.
כעת נניח כי הטענה נכונה עבור  כלשהו, כלומר מתקיים
כלשהו, כלומר מתקיים 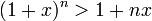 .
.
נוכיח עבור 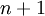 מהנחת האינדוקציה נקבל כי
מהנחת האינדוקציה נקבל כי
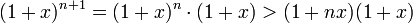
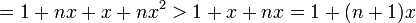
וסיימנו.
הכללה פשוטה שנייה
הכללה שבה יש שינוי בצעד האינדוקציה, הנקראת אינדוקציה שלמה: אם נוכיח עבור טענה 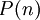 כי:
כי:
- הטענה מתקיימת עבור
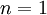 . כלומר
. כלומר 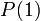 נכונה.
נכונה. - אם הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים
 (כלומר מתקיים
(כלומר מתקיים 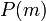 עבור
עבור 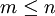 ) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר
) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר 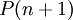 מתקיים).
מתקיים).
אז באופן דומה הטענה נכונה 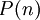 נכונה עבור
נכונה עבור 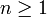 .
.
כלומר - אפשר להחליף את ההנחה שמתקיים עבור  ולהוכיח עבור
ולהוכיח עבור 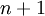 בהנחה שמתקיים עבור כל מי שקטן שווה
בהנחה שמתקיים עבור כל מי שקטן שווה  ולהוכיח עבור
ולהוכיח עבור 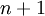 .
.
תרגיל (בד"כ נעשה בהרצאה)
כל מספר טבעי 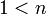 ניתן להציגו כמכפלה של מספרים ראשוניים.
ניתן להציגו כמכפלה של מספרים ראשוניים.
הוכחה:
עבור 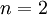 זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
כעת נניח שהטענה נכונה לכל 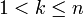 ונוכיח עבור
ונוכיח עבור 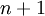 .
.
אם 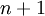 ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
אחרת 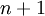 מתפרק למכפלה
מתפרק למכפלה 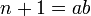 כאשר
כאשר 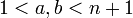 לפי הנחת האינדוקציה
לפי הנחת האינדוקציה 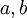 מתפרקים למכפלה של מספרים ראשוניים
מתפרקים למכפלה של מספרים ראשוניים
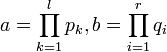 כאשר
כאשר 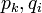 ראשוניים.
ראשוניים.
אזי 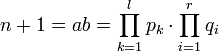 וסיימנו.
וסיימנו.
תרגיל
שאלת השוקולוד.
תרגילים יותר מעניינים
תרגיל
יהא  פסוק. נגדיר בעזרת אינדוקציה פסוקים:
פסוק. נגדיר בעזרת אינדוקציה פסוקים:
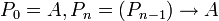
הוכיחו כי 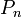 טאוטולוגיה כאשר
טאוטולוגיה כאשר  אי-זוגי.
אי-זוגי.
פתרון:
נוכיח באינדוקציה כי לכל  אי-זוגי, הפסוק
אי-זוגי, הפסוק 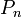 הוא טאוטולוגיה. בדיקה: עבור
הוא טאוטולוגיה. בדיקה: עבור 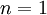 , הפסוק הוא
, הפסוק הוא 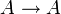 . הוא אכן טאוטולוגיה.
. הוא אכן טאוטולוגיה.
צעד: כעת, נניח את נכונות הטענה עבור  אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר
אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר 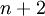 .
.
מתקיים: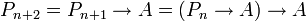 נראה כי זו אכן טאוטולוגיה. ראשית, לפי ההנחה,
נראה כי זו אכן טאוטולוגיה. ראשית, לפי ההנחה, 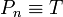 לכל ערך של
לכל ערך של  .
.
- אם
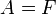 , נקבל
, נקבל 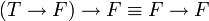 - אכן אמת.
- אכן אמת.
- אם
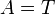 , נקבל
, נקבל 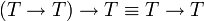 - אכן אמת.
- אכן אמת.
וסיימנו באינדוקציה.
תרגיל
יהיו 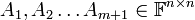 מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחה
מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחה
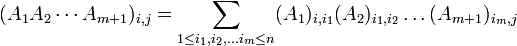
הוכחה (באינדוקציה על מספר המטריצות):
עבור 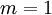 זה ההגדרה של כפל בין 2 מטריצות.
זה ההגדרה של כפל בין 2 מטריצות.
כעת, נניח שהטענה נכונה עבור 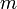 כלשהו. נוכיח נכונות עבור
כלשהו. נוכיח נכונות עבור 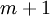 .
.
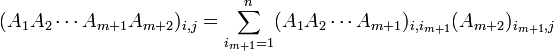
לפי הנחת האינדוקציה נמשיך:
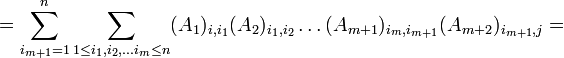
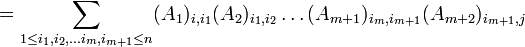
וסיימנו.
אזהרה
אינדוקציה היא כלי חזק אך יש לשים לב כי משתמשים בו נכון.
דוגמה מפורסמת להוכחת שגויה באינדוקציה היא הדוגמה הבאה:
טענה: כל קבוצה של סוסים לא ריקה מכילה סוסים מצבע יחיד.
"הוכחה": נוכיח בעזרת אינדוקציה על מספר האיברים בקבוצת הסוסים.
עבור 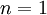 אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד.
אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד.
כעת נניח כל קבוצה עם  סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל
סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל 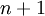 .
.
תהא 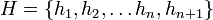 קבוצה עם
קבוצה עם 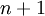 סוסים אזי לפי הנחת האינדוקציה
סוסים אזי לפי הנחת האינדוקציה
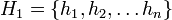 ו-
ו-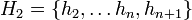 הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל
הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל  ),
ולכן כל הסוסים ב-
),
ולכן כל הסוסים ב-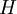 גם כן בעלי צבע יחיד (כי יש חפיפה בין
גם כן בעלי צבע יחיד (כי יש חפיפה בין 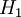 ובין
ובין 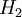 ).
).
חישבו איפה השגיאה (רמז: במעבר מ 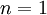 ל
ל 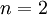 ).
).