הבדלים בין גרסאות בדף "84-172 מתמטיקה לכימאים ב/סילבוס"
מתוך Math-Wiki
(←מבחנים לדוגמא) |
(←מבחנים לדוגמא) |
||
| (21 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
=מבחנים לדוגמא= | =מבחנים לדוגמא= | ||
| + | *[[מדיה:84172Meth20Exercises.pdf|תרגילים עם פתרונות ממגוון טכניקות הנלמדות בקורס]] | ||
| + | |||
| + | *[[מדיה:84172Meth21A.pdf|מועד א' תשפ"א]], [[מדיה:84172Meth21ASol.pdf|פתרון]] | ||
| + | *[[מדיה:84172Meth21B.pdf|מועד ב' תשפ"א]], [[מדיה:84172Meth21BSol.pdf|פתרון]] | ||
| + | *[[מדיה:84172Meth22A.pdf|מועד א' תשפ"ב]], [[מדיה:84172Meth22ASol.pdf|פתרון]] | ||
| + | *[[מדיה:84172Meth22B.pdf|מועד ב' תשפ"ב]] | ||
| + | *[[מדיה:84172Meth23A.pdf|מועד א' תשפ"ג]], [[מדיה:84172Meth23ASol.pdf|פתרון]] | ||
| + | |||
| + | |||
| + | ===בחנים=== | ||
| + | *[[מדיה:84172Meth21Quiz.pdf|בוחן תשפ"א]], [[מדיה:84172Meth21QuizSol.pdf|פתרון]] | ||
| + | *[[מדיה:84172Meth22Quiz.pdf|בוחן תשפ"ב]] | ||
| + | *[[מדיה:84172Meth23Quiz.pdf|בוחן תשפ"ג]] | ||
| + | |||
| + | ===מבחנים מהעבר=== | ||
*[[מדיה:84172Meth20Exm.pdf|מבחן לדוגמא תש"ף]] | *[[מדיה:84172Meth20Exm.pdf|מבחן לדוגמא תש"ף]] | ||
*[[מדיה:84172Meth20A.pdf|מבחן מועד א' תש"ף]] | *[[מדיה:84172Meth20A.pdf|מבחן מועד א' תש"ף]] | ||
*[[מדיה:84172Meth20B.pdf|מבחן מועד ב' תש"ף]] | *[[מדיה:84172Meth20B.pdf|מבחן מועד ב' תש"ף]] | ||
| + | |||
| + | =לוח ההרצאות= | ||
| + | *[https://drive.google.com/drive/folders/1dzLayvXbvr3AzPmzowEoQDBjW-xLDH3P?usp=sharing הלוח] | ||
=נושאי הרצאות= | =נושאי הרצאות= | ||
כאן יופיעו נושאי ההרצאות המשוערים לסמסטר. | כאן יופיעו נושאי ההרצאות המשוערים לסמסטר. | ||
| − | ==חלק 1: | + | ==חלק 1: שדות, מערכות משוואות ומטריצות== |
| + | |||
===שדות=== | ===שדות=== | ||
*מושג השדה, המספרים המרוכבים | *מושג השדה, המספרים המרוכבים | ||
| + | <videoflash>3SAV7M1gJxM</videoflash> | ||
| + | |||
| + | |||
| + | <videoflash>aDPMK03MCLg</videoflash> | ||
| + | |||
| + | להרחבה ראו פרק 1 בקישור [[אלגברה לינארית - ארז שיינר|https://linear.math-wiki.com]] | ||
| + | |||
| + | ===מטריצות=== | ||
| + | |||
| + | |||
| + | *פתרון מערכות משוואות באמצעות מטריצות. | ||
| + | *דרגת מטריצה. | ||
| + | *מציאת כמות פתרונות למערכת משוואות. | ||
| + | *מערכת משוואות עם פרמטר. | ||
| + | |||
| + | <videoflash>xtoSEf5__3g</videoflash> | ||
| + | |||
| + | |||
| + | *כפל מטריצות. | ||
| + | *מטריצות הופכיות. | ||
| + | |||
| + | ==חלק 2: וקטורים ופונקציות לינאריות== | ||
===מרחבים וקטוריים ומכפלה פנימית=== | ===מרחבים וקטוריים ומכפלה פנימית=== | ||
*מרחבים וקטוריים (חיבור וקטורים וכפל בסקלר) | *מרחבים וקטוריים (חיבור וקטורים וכפל בסקלר) | ||
| + | |||
| + | <videoflash>wd1XcxGymM0</videoflash> | ||
| + | |||
| + | <videoflash>QSCKMisk4pI</videoflash> | ||
| + | |||
| + | |||
*מכפלה פנימית (סקלרית) והנורמה המושרית. | *מכפלה פנימית (סקלרית) והנורמה המושרית. | ||
| + | |||
| + | <math>v\cdot w = |v||u|\cos(\theta)</math> | ||
| + | |||
| + | <videoflash>MU45juH2U_c</videoflash> | ||
| + | |||
| + | |||
*נבחן כל אחת מהפעולות באופן אלגברי ובאופן גאומטרי. | *נבחן כל אחת מהפעולות באופן אלגברי ובאופן גאומטרי. | ||
*אי שיוויון קושי-שוורץ | *אי שיוויון קושי-שוורץ | ||
| + | *בסיס הוא קבוצת וקטורים המייצרת את הקבוצה, ואין בה דבר מיותר. | ||
| + | *מימד הוא מספר האיברים בבסיס. | ||
===העתקות לינאריות=== | ===העתקות לינאריות=== | ||
*פונקציות לינאריות | *פונקציות לינאריות | ||
| + | **<math>T(x,y)=\left(\frac{x-y}{\sqrt{2}},\frac{x+y}{\sqrt{2}}\right)</math> סיבוב נגד כיוון השעון בזוית 45 מעלות. | ||
| + | **<math>T(x,y)=\left(\frac{x+y}{2},\frac{x+y}{2}\right)</math> היטל על הישר y=x. | ||
| + | |||
| + | |||
*גרעין ותמונה (מקיימים תכונות של תתי מרחב) | *גרעין ותמונה (מקיימים תכונות של תתי מרחב) | ||
| − | + | ===הצגת פונקציות לינאריות באמצעות מטריצות=== | |
| − | + | ||
| + | <videoflash>jU5KHYC2E7s</videoflash> | ||
| − | |||
| − | |||
| − | |||
*גרעין זו ההצגה האלגברית, תמונה היא ההצגה הפרמטרית של ישרים ומישורים. | *גרעין זו ההצגה האלגברית, תמונה היא ההצגה הפרמטרית של ישרים ומישורים. | ||
| − | |||
| − | |||
| − | |||
| − | + | <videoflash>N-NLiHVo3_0</videoflash> | |
| + | ==חלק 3: לכסון מטריצות== | ||
===לכסון מטריצות=== | ===לכסון מטריצות=== | ||
| שורה 50: | שורה 104: | ||
*אלגוריתם ללכסון מטריצה. | *אלגוריתם ללכסון מטריצה. | ||
| − | + | ==חלק 4: חדו"א בשני משתנים== | |
| − | ==חלק | + | |
===מבוא=== | ===מבוא=== | ||
*גרף מהצורה <math>z=f(x,y)</math> | *גרף מהצורה <math>z=f(x,y)</math> | ||
| שורה 58: | שורה 111: | ||
===גזירות=== | ===גזירות=== | ||
*נגזרות חלקיות | *נגזרות חלקיות | ||
| − | |||
*מישור משיק | *מישור משיק | ||
| − | |||
| − | |||
*נגזרות כיווניות והגרדיאנט | *נגזרות כיווניות והגרדיאנט | ||
| − | |||
| − | |||
| − | |||
| − | |||
===בעיות קיצון=== | ===בעיות קיצון=== | ||
| שורה 72: | שורה 118: | ||
*קיצון עם אילוץ | *קיצון עם אילוץ | ||
| − | ==חלק | + | ==חלק 5: אינטגרלים כפולים ומשולשים== |
*אינטגרלים כפולים ומשולשים ומשמעותם | *אינטגרלים כפולים ומשולשים ומשמעותם | ||
*החלפת סדר האינטגרציה | *החלפת סדר האינטגרציה | ||
*שינוי קואורדינטות | *שינוי קואורדינטות | ||
גרסה אחרונה מ־08:47, 27 ביולי 2023
תוכן עניינים
מבחנים לדוגמא
בחנים
מבחנים מהעבר
לוח ההרצאות
נושאי הרצאות
כאן יופיעו נושאי ההרצאות המשוערים לסמסטר.
חלק 1: שדות, מערכות משוואות ומטריצות
שדות
- מושג השדה, המספרים המרוכבים
להרחבה ראו פרק 1 בקישור https://linear.math-wiki.com
מטריצות
- פתרון מערכות משוואות באמצעות מטריצות.
- דרגת מטריצה.
- מציאת כמות פתרונות למערכת משוואות.
- מערכת משוואות עם פרמטר.
- כפל מטריצות.
- מטריצות הופכיות.
חלק 2: וקטורים ופונקציות לינאריות
מרחבים וקטוריים ומכפלה פנימית
- מרחבים וקטוריים (חיבור וקטורים וכפל בסקלר)
- מכפלה פנימית (סקלרית) והנורמה המושרית.
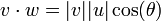
- נבחן כל אחת מהפעולות באופן אלגברי ובאופן גאומטרי.
- אי שיוויון קושי-שוורץ
- בסיס הוא קבוצת וקטורים המייצרת את הקבוצה, ואין בה דבר מיותר.
- מימד הוא מספר האיברים בבסיס.
העתקות לינאריות
- פונקציות לינאריות
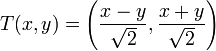 סיבוב נגד כיוון השעון בזוית 45 מעלות.
סיבוב נגד כיוון השעון בזוית 45 מעלות.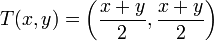 היטל על הישר y=x.
היטל על הישר y=x.
- גרעין ותמונה (מקיימים תכונות של תתי מרחב)
הצגת פונקציות לינאריות באמצעות מטריצות
- גרעין זו ההצגה האלגברית, תמונה היא ההצגה הפרמטרית של ישרים ומישורים.
חלק 3: לכסון מטריצות
לכסון מטריצות
- מהו לכסון מטריצות ולמה הוא טוב (למשל העלאת מטריצה בחזקה).
- פולינום אופייני, ערכים עצמיים, וקטורים עצמיים.
- אלגוריתם ללכסון מטריצה.
חלק 4: חדו"א בשני משתנים
מבוא
- גרף מהצורה
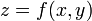
- גבולות ורציפות
גזירות
- נגזרות חלקיות
- מישור משיק
- נגזרות כיווניות והגרדיאנט
בעיות קיצון
- קיצון מקומי
- קיצון עם אילוץ
חלק 5: אינטגרלים כפולים ומשולשים
- אינטגרלים כפולים ומשולשים ומשמעותם
- החלפת סדר האינטגרציה
- שינוי קואורדינטות