הבדלים בין גרסאות בדף "88-101 חשיבה מתמטית"
(←חומר נוסף) |
(←חוקי דה-מורגן) |
||
| שורה 123: | שורה 123: | ||
'''תרגיל'''. כתוב את הפסוק המתאר שלשה '''לא חוקית''' בSET. | '''תרגיל'''. כתוב את הפסוק המתאר שלשה '''לא חוקית''' בSET. | ||
| + | |||
| + | '''תרגיל'''. בניסוי מפורסם בתורת ההחלטות, מציגים לנבדק ארבעה כרטיסים שבגבם הסימנים A, P, 2, 3. על כל כרטיס יש אות ומספר. אלו כרטיסים יש להפוך על-מנת לבדוק את הטענה "אם בצד אחד של הכרטיס יש אות ניקוד (AEIOU) אז בצידו האחר יש מספר זוגי?" רוב גדול של האנשים עונים שיש להפוך את הכרטיס הראשון והשלישי. מה התשובה הנכונה? | ||
== תחשיב פרידקטים == | == תחשיב פרידקטים == | ||
גרסה מ־22:34, 11 ביולי 2011
הסדנא בחשיבה מתמטית מציגה את עקרונות היסוד של הלוגיקה המתמטית.
תוכן עניינים
הצרנה
הצרנה היא תרגום של פסוק או טיעון יומיומי או מתמטי לשפה לוגית מדוייקת, על-פי צורתו, תוך התעלמות מתוכנו. לאחר שהפסוק תורגם, אפשר להפעיל עליו כלים לוגיים סטנדרטיים על-מנת לבחון אותו, להעביר אותו לצורה שקולה, לעמת אותו עם פסוקים אחרים, וכדומה.
- "אם לא תגמור מהצלחת, יבוא שוטר".
כדי לטפל בפסוק כזה, עלינו להגדיר שני אטומים: A="תגמור מהצלחת", B="יבוא שוטר". הפסוק קובע "אם לא A אז B". כך אפשר לראות מיד שיש לו אותו מבנה לוגי, אותה צורה, כמו לפסוק הבא:
- "אם לא נכלכל את צעדינו בתבונה, נמצא את עצמנו מול שוקת שבורה".
(אם לא A אז B, כאשר A="נכלכל את צעדינו בתבונה" ו-B="נמצא את עצמנו מול שוקת שבורה").
הדוגמאות יכולות להיות מסובכות בהרבה:
- "כאשר אני עייף ורעב אני נעשה עצבני, או שאני הולך לישון; אבל אם אני עצבני ולא עייף, אז אני רעב". (כלומר, עבור הביטויים המתאימים A,B,C,D: (אם A וגם B אז (C או D)), וגם (אם C ולא A אז לא B)).
- חוקי המשחק SET: על השולחן מונחים שנים-עשר קלפים, לכל קלף במשחק יש שלוש תכונות: צורה, צבע, מספר ומילוי. על השחקנים למצוא שלישיות חוקיות; שלישיה חוקית הינה שלישיה של קלפים אשר כל תכונה שלהם בנפרד שווה בכולם או שונה בכולם. לכן שלישיה הינה חוקית אם (((הצבע של שלושת הקלפים זהה) או (לכל קלף יש צבע אחר)) וגם ((המילוי של שלושת הקלפים זהה) או (לכל קלף יש מילוי אחר))וגם ((המספר של שלושת הקלפים זהה) או (לכל קלף יש מספר אחר)) וגם ((הצורה של שלושת הקלפים זהה) או (לכל קלף יש צורה אחרת))). (כלומר, עבור הביטויים המתאימים A,B,C,D,E,F,H,I: שלישיה הינה חוקית אם ((A או B) וגם (C או D) וגם (E או F) וגם (H או I))).
הצרנה היא כלי מתמטי ולא ספרותי, ותוך כדי יצירת ביטוי חד-משמעי היא עשויה לאבד את המשמעויות העדינות של המשפט המקורי. לדוגמא, מצרינים
- "ירד גשם ובכל זאת היה חם בחוץ" ו-
- "ירד גשם והיה חם בחוץ"
באותה צורה ("A וגם B"). המשמעות המרומזת ("בדרך כלל A גורר את השלילה של B") נעלמת.
תרגיל. הצרן: למדתי היטב למבחן, ואף על פי כן נכשלתי בו.
דוגמא נוספת:
- "ערן לובש חולצה סגולה אם הוא לובש מכנסיים בצבע שחור", "כאשר ערן לובש מכנסיים בצבע שחור אז הוא לובש חולצה סגולה", "יחד עם מכנסיים בצבע שחור, ערן לובש חולצה סגולה בלבד", וכן הלאה.
תרגיל.
- לוגיקן הלך לאכול במסעדת גורמה. בסיום הארוחה הוא ניגש אל המלצר בתחילת הארוחה ואומר לו: "תקבל טיפ אם תגיש את האוכל חם, או אם האוכל יגיע קר אבל בזמן. כמו כן הטיפ שלך תלוי במידת אדיבותך: אם האוכל לא טעים ולא בררת איתי לגבי טעמו, לא תקבל טיפ. דבר אחד עשוי להציל את הטיפ שלך - אם האוכל יהיה קר וטעים ויגיע באיחור, תוכל לפצות אותי על ידי קינוח חינם". הצרן את התנאי לקבלת טיפ, וחשב מה קרה בארוחה אם ידוע שהמלצר לא קיבל טיפ.
ערך אמת
ערך אמת הוא אחת משתי האפשרויות - אמת או שקר, שמסמנים לשם הקיצור T ו-F (מ-True ו-False, כמובן). אם האטומים מפורטים מספיק (מי יגמור מה ומתי מאיזו צלחת), כל אטום מקבל ערך אמת. או שתגמור מהצלחת, או שלא. או שיבוא שוטר, או שלא. אם תגמור מהצלחת, אז ערך האמת של הפסוק "תגמור מהצלחת" הוא T, ואחרת, הוא F. זו הדרך לחבר את תמונת העולם של המציאות, עם הפסוקים הלוגיים הפורמליים.
כאשר משייכים לכל אטום של פסוק לוגי ערך אמת, אפשר לחשב את ערך האמת של הפסוק עצמו. לשם כך יש להכיר את הקשרים הלוגיים הבסיסיים.
פסוקים וקשרים
וגם הוא קשר לוגי: אפשר לומר משפטים כמו "התפוח הזה אדום, וגם הצלחת ירוקה", שההצרנה שלהם היא במבנה "A וגם B". אי אפשר לומר "התפוח הזה אדום וגם", משום ש"וגם" הוא קשר בינארי - הוא מחבר שני אטומים. ערך האמת של הפסוק "A וגם B" הוא T, רק כאשר גם A וגם B הם T. בכל מקרה אחר, ערך האמת הוא F.
דוגמא. כשפוליטיקאי מבטיח "לא נעלה מסים וגם נגדיל את ההוצאה לחינוך" (שצורתו "(לא A) וגם B"), הוא יצטרך לקיים שתי הבטחות: גם לא A, וגם B.
כבר פגשנו את קשר השלילה, לא, שהוא הקשר האונארי היחיד. הפסוק המתקבל משלילת A הוא, כמובן, "לא A"; ערך האמת שלו הפוך לזה של A: אם "יבוא שוטר" הוא פסוק אמיתי, אז "לא יבוא שוטר" הוא פסוק שקרי, ולהיפך.
קשר נוסף הוא או: גם הוא קשר בינארי, המאפשר לבנות את הפסוק "A או B". פסוק כזה מקבל ערך אמת T אם אחת ההצהרות קיבלה ערך אמת T, או שתיהן.
דוגמא. כשפוליטיקאי מבטיח "לא נעלה מסים, או שנגדיל את ההוצאה לחינוך" (שצורתו "(לא A) או B"), הוא יוכל להסתפק בקיום אחת ההבטחות.
הקשר אם-אז בונה משפטים כמו "אם נגדיל את ההוצאה לחינוך, נעלה מסים": "אם A אז B". אם ערך האמת של A הוא T, אז ערך האמת של "אם A אז B" שווה לערך האמת של B: אם מבטיחים, ההצהרה "אם הבטחתי אז אקיים" נכונה אם אקיים, ולא נכונה אם לא אקיים. לעומת זאת, אם לא הבטחתי, ההצהרה נכונה בכל מקרה: כשערך האמת של A הוא F, ערך האמת של "אם A אז B" הוא T בלי קשר לערך האמת של B. זהו הסכם חשוב, גם אם קצת קשה לקבל אותו בתחילה. נראה עוד כמה דוגמאות.
- "אם לסבתא היו גלגלים היא היתה אוטובוס". זהו פסוק מהצורה "אם A אז B", כאשר A="לסבתא יש גלגלים", ו-B="סבתא היא אוטובוס". בהנחה ששתי הטענות שקריות, הפסוק עצמו הוא נכון: אם היו לסבתא גלגלים אז היא היתה אוטובוס, אבל אין לה, כך שזה בכלל לא חשוב אם היא אוטובוס או לא; הפסוק אמיתי.
תרגיל. בדוק שאם ערך האמת של B הוא T, אז ערך האמת של "אם A אז B" הוא תמיד T. קבע מתי ערך האמת של "אם A אז B" הוא T, אם ידוע שערך האמת של B הוא F.
דוגמא. הפסוק "אם יש עננים אז יורד גשם" אינו אמיתי, משום שיתכן שיהיו עננים בלי שירד גשם. לעומת זאת הפסוק "אם יורד גשם אז יש עננים" הוא אמיתי. את הפסוק השני, האמיתי, אפשר לנסח בצורות נוספות: "יש עננים אם יורד גשם" (מוכרחים להיות עננים אם יורד גשם), וגם "יורד גשם רק אם יש עננים" (כל אימת שיורד גשם, מוכרחים להיות עננים).
נסכם: הפסוקים "אם A אז B", "B אם A" ו"A רק אם B" אומרים אותו הדבר.
לכן, במקום להגיד "אם B אז A, וגם אם A אז B", אפשר לומר "A אם B, ו-A רק אם B", ובקיצור "A אם ורק אם B". זהו הקשר הבינארי האחרון שנציג בשם: אם ורק אם. ערך האמת של "A אם ורק אם B" הוא T בדיוק כאשר ערכי האמת של A ושל B שווים. דוגמא. משולש הוא ישר זווית ושווה שוקיים אם ורק אם יש לו שתי זוויות של 45 מעלות.
סימוני הקשרים
לקשרים הסטנדרטיים יש גם סימון סטנדרטי, שיש להכיר ולזכור.
- במקום "לא A" כותבים
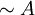 או
או 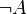 .
. - במקום "A וגם B" כותבים
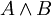 .
. - במקום "A או B" כותבים
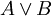 .
. - במקום "אם A אז B" כותבים
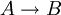 ; מותר גם
; מותר גם 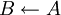 .
. - במקום "A אם ורק אם B" כותבים
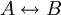 .
.
פסוקים מורכבים
את הקשרים שפגשנו (לא, וגם, או, אם-אז, אם-ורק-אם) אפשר להפעיל לא רק על אטומים, אלא גם על פסוקים.
דוגמא. אם אדם הוא מאושר אם ורק אם הוא לומד דברים חדשים, אז אדם שאינו לומד דברים חדשים אינו מאושר. (שמצרינים ל"אם (A אם ורק אם B), אז (אם לא B, אז לא A)").
פסוק הוא רצף של תווים, שכל אחד מהם הוא או אחד האטומים (מקובל להניח שעומדת לרשותנו אספקה אינסופית של אטומים), או אחד מסימני הקשרים, או אחד הסימנים המיוחדים "(" ו")" שתפקידם להבטיח קריאה חד-משמעית של הפסוק. לדוגמא, הפסוק 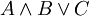 אינו ניתן לקריאה באופן ברור: אין לדעת האם הכוונה היא ל-
אינו ניתן לקריאה באופן ברור: אין לדעת האם הכוונה היא ל-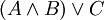 או ל-
או ל-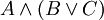 . (תרגיל: מצא ערכי אמת של A,B,C שיתנו ערכי אמת שונים לשני הפסוקים האחרונים). הכלל במקרה של ספק הוא פשוט: עדיף לבזבז מאה זוגות סוגריים מיותרים, מאשר להשמיט זוג סוגריים חיוני אחד.
. (תרגיל: מצא ערכי אמת של A,B,C שיתנו ערכי אמת שונים לשני הפסוקים האחרונים). הכלל במקרה של ספק הוא פשוט: עדיף לבזבז מאה זוגות סוגריים מיותרים, מאשר להשמיט זוג סוגריים חיוני אחד.
כמובן שלא כל רצף של סימנים הוא פסוק. "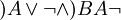 " אינו פסוק. אפשר להגדיר מהו פסוק "באינדוקציה על המבנה":
" אינו פסוק. אפשר להגדיר מהו פסוק "באינדוקציה על המבנה":
- כל פסוק הוא או אטום, או שיש לו הצורה
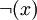 כאשר x הוא פסוק, או הצורה
כאשר x הוא פסוק, או הצורה 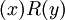 , כאשר R הוא אחד מסימני הקשרים הבינאריים, ו-x,y הם פסוקים.
, כאשר R הוא אחד מסימני הקשרים הבינאריים, ו-x,y הם פסוקים.
הגדרה זו היא אחת מאבני היסוד של הלוגיקה הפסוקית, המטפלת בפסוקים באופן פורמלי. זהו רק הסוג הראשון של פסוקים שאנו פוגשים - בהמשך נכיר שני סוגים מתוחכמים יותר.
תרגיל. הוכח, באינדוקציה על אורך הפסוק, שאפשר לבנות מכונה שתזהה האם רצף של תווים הוא פסוק של הלוגיקה הפסוקית, או לא (הנח שהמכונה יודעת לזהות אטומים).
טבלאות אמת
טבלת אמת מאפשרת לטפל בפסוק על-ידי בחינת כל האפשרויות לערכי אמת של האטומים המעורבים בו. טכנית, אם בפסוק יש n אטומים, הטבלה מורכבת מ-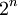 שורות, שבכל אחת מהן מקצים אפשרות אחרת לערכי האמת של האטומים. למשל, בטבלת האמת של
שורות, שבכל אחת מהן מקצים אפשרות אחרת לערכי האמת של האטומים. למשל, בטבלת האמת של 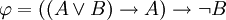 יש ארבע שורות, המתאימות לערכי האמת TT, TF, FT, FF עבור האטומים AB. בטבלה יש להוסיף גם את ערך האמת של כל תת-פסוק (במקרה דנן,
יש ארבע שורות, המתאימות לערכי האמת TT, TF, FT, FF עבור האטומים AB. בטבלה יש להוסיף גם את ערך האמת של כל תת-פסוק (במקרה דנן, 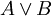 ו-
ו- 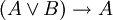 ), ובסופו של דבר את ערך האמת של הפסוק עצמו.
), ובסופו של דבר את ערך האמת של הפסוק עצמו.
פסוק שערך האמת שלו הוא תמיד T, לכל הצבה של ערכי אמת באטומים, נקרא טאוטולוגיה. פסוק שערך האמת שלו הוא תמיד F נקרא סתירה.
לטאוטולוגיות חשיבות מיוחדת בלוגיקה, משום שהם מבטאות אמת צורנית אוניברסלית, שאינה תלויה בהצבת ערכי האמת. (ראו גם [1]).
דוגמא. הפסוק 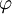 שהוזכר לעיל הוא טאוטולוגיה. הוא קובע שאם מההנחה "A או B" אפשר להסיק את A, אז B מוכרח להיות שקרי.
שהוזכר לעיל הוא טאוטולוגיה. הוא קובע שאם מההנחה "A או B" אפשר להסיק את A, אז B מוכרח להיות שקרי.
תרגיל. אם 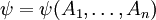 הוא פסוק טאוטולוגי התלוי באטומים
הוא פסוק טאוטולוגי התלוי באטומים 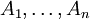 , אז כל פסוק המתקבל מהצבה של פסוקים כלשהם
, אז כל פסוק המתקבל מהצבה של פסוקים כלשהם 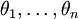 במקום האטומים (באופן עקבי), גם הוא טאוטולוגי.
במקום האטומים (באופן עקבי), גם הוא טאוטולוגי.
חשוב להכיר טאוטולוגיות בסיסיות, ועוד יותר חשוב לדעת כיצד בודקים האם פסוק הוא טאוטולוגי, ולזהות פסוקים שאינם טאוטולוגיות. דוגמאות. להלן כמה טאוטולוגיות שקל לבדוק:
-
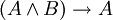 (כלומר, אם A וגם B, אז בפרט A);
(כלומר, אם A וגם B, אז בפרט A); -
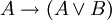 (אם A, אז בוודאי מתקיים A או B);
(אם A, אז בוודאי מתקיים A או B); -
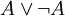 (זהו "כלל השלישי הנמנע": או שהתפוח אדום או שאינו אדום (כמובן, בתנאי שמגדירים היטב מתי תפוח הוא אדום));
(זהו "כלל השלישי הנמנע": או שהתפוח אדום או שאינו אדום (כמובן, בתנאי שמגדירים היטב מתי תפוח הוא אדום)); -
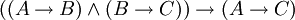 (אם מ-A נובע B ומ-B נובע C, אז מ-A נובע C).
(אם מ-A נובע B ומ-B נובע C, אז מ-A נובע C).
אפשר להמציא עוד טאוטולוגיות כהנה וכהנה. תרגיל. הסבר מדוע פסוק שמופיעים בו רק הקשרים הלוגיים "או" ו"וגם" אינו יכול להיות טאוטולוגיה.
הגדרתו של הקשר הלוגי "אם ורק אם" מובילה אותנו להגדרה שימושית:
הגדרה. הפסוקים 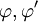 הם שקולים אם הפסוק
הם שקולים אם הפסוק 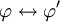 הוא טאוטולוגיה. במקרה כזה מסמנים
הוא טאוטולוגיה. במקרה כזה מסמנים 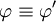 .
.
דוגמאות.
-
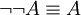
-
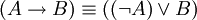 .
. -
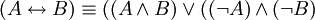 .
. -
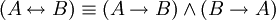 .
. -
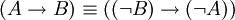 .
.
משפט. כל פסוק לוגי שקול לפסוק שבו מופיעים רק קשר השלילה והקשרים "או" ו"וגם".
חוקי דה-מורגן
חשוב לדעת לנסח במדוייק את השלילה של פסוק נתון. הדוגמאות הבסיסיות מסוג זה נקראות כללי דה-מורגן:
-
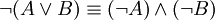 .
. -
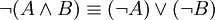 .
.
משפט. כל פסוק לוגי שקול להצבת האטומים 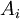 ושלילתם
ושלילתם 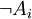 , בפסוק שבו מופיעים רק הקשרים "או" ו"וגם".
, בפסוק שבו מופיעים רק הקשרים "או" ו"וגם".
תרגיל. כתוב את הפסוק המתאר שלשה לא חוקית בSET.
תרגיל. בניסוי מפורסם בתורת ההחלטות, מציגים לנבדק ארבעה כרטיסים שבגבם הסימנים A, P, 2, 3. על כל כרטיס יש אות ומספר. אלו כרטיסים יש להפוך על-מנת לבדוק את הטענה "אם בצד אחד של הכרטיס יש אות ניקוד (AEIOU) אז בצידו האחר יש מספר זוגי?" רוב גדול של האנשים עונים שיש להפוך את הכרטיס הראשון והשלישי. מה התשובה הנכונה?
תחשיב פרידקטים
הלוגיקה שלמדנו עד כה מאפשרת לטפל רק במצבים קונקרטיים: הצלחת הזו אדומה, הכלב הזה נובח. כלים אלו אינם מאפשרים לנסח אפילו טענות פשוטות כמו
- לכל מספר יש מספר גדול יותר
או
- מישהו כתב את הדפים האלה.
כדי להצרין טענות כאלה, המופיעות במתמטיקה בכל מקום, עלינו לרכוש שני כלים חדשים: פרדיקטים וכמתים.
פרדיקטים
בלוגיקה מתמטית, פרדיקט הוא פונקציה המקבלת משתנה או כמה משתנים, ומחזירה ערך אמת (T או F). זוהי הכללה של האטומים שפגשנו קודם לכן, שאינם אלא פרידקטים ללא משתנים. פרדיקט הוא למעשה תכונה - של משתנה בודד או של כמה משתנים.
דוגמאות.
- כדי לומר "התפוח הזה צהוב", מגדירים פרדיקט
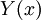 , עם משתנה אחד, המחזיר את הערך T כאשר x צהוב, ואת הערך F בכל מקרה אחר.
, עם משתנה אחד, המחזיר את הערך T כאשר x צהוב, ואת הערך F בכל מקרה אחר. - כדי לומר "דפנה היא אמא של יובל", אפשר להגדיר פרדיקט
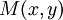 המקבל ערך T כאשר x היא אמא של y. יש להציב את דפנה במקום x ואת יובל במקום y.
המקבל ערך T כאשר x היא אמא של y. יש להציב את דפנה במקום x ואת יובל במקום y. - כדי לומר "2 קטן מ-7", יש להגדיר פרדיקט של סדר,
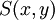 , המקבל ערך T כאשר
, המקבל ערך T כאשר 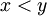 . מכיוון שיחס הסדר כבר זכה לשם מוכר, אפשר להשתמש בו ישירות, ולכתוב את הפרדיקט
. מכיוון שיחס הסדר כבר זכה לשם מוכר, אפשר להשתמש בו ישירות, ולכתוב את הפרדיקט 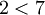 .
.
תרגיל. הגדירו פרדיקטים והצבות במשתנים, כך שהפסוק 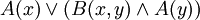 יצרין את "אורן או חברתו קארין לומדים לוגיקה".
יצרין את "אורן או חברתו קארין לומדים לוגיקה".
הפסוקים מהסוג הראשון שפגשנו הורכבו מאטומים המקושרים על-ידי הקשרים הלוגיים. הסוג השני הוא בעל אותו מבנה, אלא שבמקום אטומים מותר להשתמש בפרדיקטים עם משתנים כלשהם. התוצאה, כמו בסוג הראשון, היא פסוק לוגי - אלא שכאן התוצאה תלויה במשתנים. לכן, במקום לסמן את הפסוק באות בודדת, נכתוב 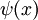 או
או 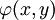 .
.
חשוב להבין שערך האמת של פסוק המערב בפרדיקטים, כמו 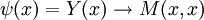 ("אם x צהוב, אז הוא אמא של עצמו") תלוי בערך המשתנה: בדוגמא הזו, אם x הוא אדם צהוב, הפסוק מקבל את הערך F, ואם x הוא אדם שאינו צהוב, ערך האמת הוא T.
("אם x צהוב, אז הוא אמא של עצמו") תלוי בערך המשתנה: בדוגמא הזו, אם x הוא אדם צהוב, הפסוק מקבל את הערך F, ואם x הוא אדם שאינו צהוב, ערך האמת הוא T.
גמישות זו עדיין אינה מאפשרת לנסח טענות כלליות, כמו "אף אדם אינו אמא של עצמו". לשם כך יש צורך בכמתים.
כמתים
פסוקים עם כמתים
הכמתים, המציינים תחולה של משתנה, הם תוספת חיונית למערך הקשרים שלנו. יש שני כמתים: "לכל", המסומן באות 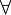 (זוהי A הפוכה, קיצור של המלה All); ו"קיים", המסומן באות
(זוהי A הפוכה, קיצור של המלה All); ו"קיים", המסומן באות 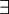 (E הפוכה, קיצור של Exists). כשבונים פסוק עם כמתים, מותר לקחת פסוק קיים (הכולל פרדיקטים, שבהם x הוא משתנה), ולבנות:
(E הפוכה, קיצור של Exists). כשבונים פסוק עם כמתים, מותר לקחת פסוק קיים (הכולל פרדיקטים, שבהם x הוא משתנה), ולבנות:
-
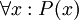 - מקבל ערך אמת T אם הפסוק
- מקבל ערך אמת T אם הפסוק 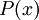 מקבל ערך אמת לכל הצבה של x.
מקבל ערך אמת לכל הצבה של x. -
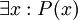 - מקבל ערך אמת T אם יש הצבה של x כך שהפסוק
- מקבל ערך אמת T אם יש הצבה של x כך שהפסוק 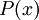 מקבל ערך אמת.
מקבל ערך אמת.
דוגמא. את הפסוק "אין מספר גדול ביותר" אפשר להצרין באופן פשטני, כך: 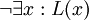 , כאשר
, כאשר 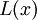 הוא הפרדיקט "x הוא מספר גדול ביותר". הצרנה מעט יותר מתוחכמת תגדיר את הפרדיקט
הוא הפרדיקט "x הוא מספר גדול ביותר". הצרנה מעט יותר מתוחכמת תגדיר את הפרדיקט 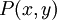 שפירושו "x<y", ותצרין ל-
שפירושו "x<y", ותצרין ל-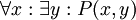 , כלומר, לכל מספר יש מספר הגדול ממנו.
, כלומר, לכל מספר יש מספר הגדול ממנו.
זהו הסוג השלישי (והאחרון עבורנו) של פסוקים לוגיים. נסכם: פסוק הוא או פרדיקט (לרבות אטומים, שהם פרדיקטים ללא משתנים), או חיבור של פסוקים קצרים יותר באמצעות קשרים לוגיים, או החלה של כמת על פסוק קצר יותר.
גם לאחר ההרחבה הזו, בכל פסוק יש "פעולה אחרונה": הקשר האחרון או הכמת האחרון שהופעל כדי ליצור את הפסוק. לדוגמא:
- הפעולה האחרונה ב-
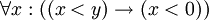 ("לכל x, אם x קטן מ-y אז x שלילי") היא הכמת הכולל על x; לעומת זאת הפעולה האחרונה ב-
("לכל x, אם x קטן מ-y אז x שלילי") היא הכמת הכולל על x; לעומת זאת הפעולה האחרונה ב- 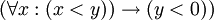 ("אם כל x הוא קטן מ-y, אז y שלילי") היא הקשר "אם-אז".
("אם כל x הוא קטן מ-y, אז y שלילי") היא הקשר "אם-אז".
את החשיבות בזיהוי הפעולה האחרונה נוכל להסביר כשנגיע לשלילה של פסוקים.
פסוקים אמיתיים
לפסוקים שיש בהם כמתים אי אפשר לבנות טבלאות אמת, משום שלצד האטומים המקבלים רק שני ערכי אמת אפשריים, יש בהם משתנים העשויים לעבור על-פני מספר אינסופי של אפשרויות. לכן הלוגיקה המטפלת בפסוקים עם כמתים (הנקראת "לוגיקה מסדר ראשון") מורכבת יותר מן הלוגיקה הפסוקית, ויש לה יכולת ביטוי רחבה יותר. גם בלוגיקה זו אומרים ששני פסוקים 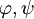 הם שקולים אם
הם שקולים אם  מקבל ערך אמת לכל הצבה של המשתנים המעורבים.
מקבל ערך אמת לכל הצבה של המשתנים המעורבים.
פסוק אמיתי הוא כזה שמתקיים לכל בחירה של הפרדיקטים ולכל הצבה במשתנים. כל הטאוטולוגיות הן פסוקים אמיתיים, אבל ההיפך אינו נכון. לא נכנס כאן לפרטים, שמהם מתפרנסים חוקרי הלוגיקה המתמטית.
תרגיל. קבע אלו מהפסוקים הבאים הם אמיתיים, כאשר הסימנים "לכל" ו"קיים" פירושם "לכל מספר שלם" ו"קיים מספר שלם". אם הפסוק אינו אמיתי, בחר פרדיקטים ומשתנים המדגימים זאת.
-
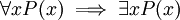 .
. -
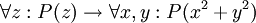 .
. -
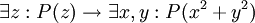 .
. -
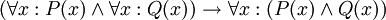 .
. -
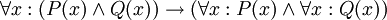 .
. -
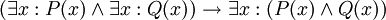 .
. -
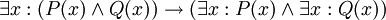 .
.
תרגיל. שכנע את עצמך באמיתיות הפסוקים הבאים:
-
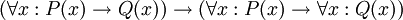 .
.
משתנים ותחולתם
אנו מגיעים לנקודה חשובה ביותר הנוגעת לשמות המשתנים. לכל כמת יש אזור תחולה. אם נכתוב למשל 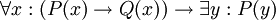 , אזור התחולה של הכמת הראשון הוא תת-הפסוק
, אזור התחולה של הכמת הראשון הוא תת-הפסוק  , ואזור התחולה של הכמת השני הוא ההופעה השניה. בתוך אזור התחולה הזה, אין כל חשיבות לשם המשתנה - אין שום הבדל בין "לכל נורה x יש מתג y כך ש-y מפעיל את x" (הצרן את הפסוק הזה), לבין "לכל נורה z יש מתג y כך ש-y מפעיל את z". לעומת זאת, הפסוק "לכל נורה x יש מתג y כך ש-y מפעיל את z".
, ואזור התחולה של הכמת השני הוא ההופעה השניה. בתוך אזור התחולה הזה, אין כל חשיבות לשם המשתנה - אין שום הבדל בין "לכל נורה x יש מתג y כך ש-y מפעיל את x" (הצרן את הפסוק הזה), לבין "לכל נורה z יש מתג y כך ש-y מפעיל את z". לעומת זאת, הפסוק "לכל נורה x יש מתג y כך ש-y מפעיל את z".
נתבונן בפרדיקט בן שני משתנים, 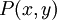 (למשל x אוהב את y). ערך האמת שלו תלוי בהצבה של x ו-y.
(למשל x אוהב את y). ערך האמת שלו תלוי בהצבה של x ו-y.
נשווה זאת לפסוק 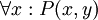 (כל x אוהב את y). בפסוק זה אי אפשר להציב את x: הפסוק למעשה אומר "כולם אוהבים את y", והתפקיד של x הוא פורמלי לחלוטין - לסמן את המשתנה העובר על כל האפשרויות. הפסוק
(כל x אוהב את y). בפסוק זה אי אפשר להציב את x: הפסוק למעשה אומר "כולם אוהבים את y", והתפקיד של x הוא פורמלי לחלוטין - לסמן את המשתנה העובר על כל האפשרויות. הפסוק 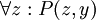 שקול לגמרי לקודם. כדי להדגיש זאת, אפשר לכתוב
שקול לגמרי לקודם. כדי להדגיש זאת, אפשר לכתוב 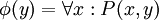 , ע ם המשתנה היחיד y.
, ע ם המשתנה היחיד y.
שימו לב לתפקיד הרגיש של x בפסוק כזה. אם נכתוב למשל 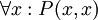 ("כל אחד אוהב את עצמו"), נקבל פסוק בעל משמעות שונה לחלוטין. אם רוצים להציב ב-
("כל אחד אוהב את עצמו"), נקבל פסוק בעל משמעות שונה לחלוטין. אם רוצים להציב ב-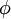 את x דווקא, מוכרחים להחליף לפני כן את המשתנה. לא נכתוב
את x דווקא, מוכרחים להחליף לפני כן את המשתנה. לא נכתוב 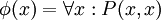 , אלא
, אלא 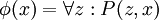 .
.
נתבונן בדוגמא נוספת. אם ידועה תכונה Q הנכונה לכל x ולכל y, כותבים 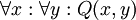 (ולפעמים, בקיצור,
(ולפעמים, בקיצור, 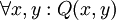 ). מכיוון שהטענה נכונה לכל x ולכל y, אפשר להציב בה ערכים בכל דרך שנרצה - כמובן שלכל x ו-y מתקיים
). מכיוון שהטענה נכונה לכל x ולכל y, אפשר להציב בה ערכים בכל דרך שנרצה - כמובן שלכל x ו-y מתקיים 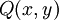 , אבל גם
, אבל גם 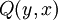 או
או 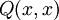 .
.
לעומת זאת, הטענה 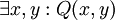 אומרת שקיימים x,y המקיימים את התכונה (מישהו נשך מישהו אחר במרפק). אנחנו לא יכולים לבחור את x,y - וגם לא להניח שיש קשר מסויים ביניהם. בפרט, לא נובע מההנחה ש-
אומרת שקיימים x,y המקיימים את התכונה (מישהו נשך מישהו אחר במרפק). אנחנו לא יכולים לבחור את x,y - וגם לא להניח שיש קשר מסויים ביניהם. בפרט, לא נובע מההנחה ש- 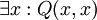 (מישהו נשך את עצמו במרפק).
(מישהו נשך את עצמו במרפק).
וריאציות וכימות יחסי
הכמתים היסודיים מאפשרים לנסח טענות סטנדרטיות נוספות.
-
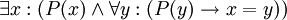 -- "קיים x המקיים את התכונה P, ובנוסף, כל y המקיים את התכונה P שווה ל-x". כלומר: "קיים x יחיד המקיים את התכונה P". לפעמים מקצרים את הפסוק הזה וכותבים
-- "קיים x המקיים את התכונה P, ובנוסף, כל y המקיים את התכונה P שווה ל-x". כלומר: "קיים x יחיד המקיים את התכונה P". לפעמים מקצרים את הפסוק הזה וכותבים 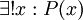 . אפשר לראות בצירוף "
. אפשר לראות בצירוף "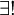 " כמת שלישי, למרות שכאמור לעיל ניתן להגדיר אותו באמצעות שני הכמתים האחרים (בנוכחות פרדיקט השוויון).
" כמת שלישי, למרות שכאמור לעיל ניתן להגדיר אותו באמצעות שני הכמתים האחרים (בנוכחות פרדיקט השוויון).
לפעמים רוצים לומר שיש אינסוף מספרים המקיימים תכונה מסויימת. אפשר לעשות זאת כך:
-
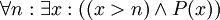 : "לכל n יש x גדול ממנו המקיים את התכונה". אם היה רק מספר סופי של מספרים המקיימים את התכונה המדוברת, אז הפסוק היה שקרי משום שאפשר היה לבחור בתור n את המספר הגדול ביותר.
: "לכל n יש x גדול ממנו המקיים את התכונה". אם היה רק מספר סופי של מספרים המקיימים את התכונה המדוברת, אז הפסוק היה שקרי משום שאפשר היה לבחור בתור n את המספר הגדול ביותר.
מאחורי כל כמת מסתתרת "קבוצה אוניברסלית", שהיא קבוצת הערכים המותרים עבור המשתנה הצמוד לכמת (מספרים ממשיים, מספרים טבעיים, פירות, אנשים). בדרך כלל הקבוצה הזו מובנת מההקשר; אם לא, יש לציין במפורש מהו טווח הערכים המתאים. לצרכי נוחות, מרשים גמישות במבנה הפסוקים, כך שאפשר יהיה לכמת "כימות יחסי". לדוגמא, מותר לכתוב
-
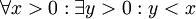 - "לכל מספר חיובי x יש מספר חיובי y הקטן ממנו", כלומר "אין מספר חיובי קטן ביותר", בתור קיצור לכתיבה המלאה
- "לכל מספר חיובי x יש מספר חיובי y הקטן ממנו", כלומר "אין מספר חיובי קטן ביותר", בתור קיצור לכתיבה המלאה 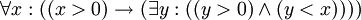 - "לכל מספר x, אם הוא חיובי, אז קיים מספר y שהוא חיובי וקטן מ-x".
- "לכל מספר x, אם הוא חיובי, אז קיים מספר y שהוא חיובי וקטן מ-x".
תרגיל. נאמר שאיבר a של קבוצת מספרים A הוא "חסם עליון" אם הוא גדול מכל איבר אחר בקבוצה. הצרן את הטענה "לקבוצה A יש חסם עליון". הצרן את הטענה "אם יש לקבוצה חסם עליון, אז הוא יחיד".
תרגיל.
- באחד התרגילים הקודמים היית אמור לאשר שהפסוק
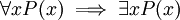 הוא אמיתי, אם הכמתים מתייחסים לקבוצת המספרים השלמים. מצא מרחב חילה של הכמתים שעבורו הפסוק אינו אמיתי (חשוב על הפסוק "כל פיל מעופף יודע קרוא וכתוב; מכאן שיש פיל מעופף היודע קרוא וכתוב").
הוא אמיתי, אם הכמתים מתייחסים לקבוצת המספרים השלמים. מצא מרחב חילה של הכמתים שעבורו הפסוק אינו אמיתי (חשוב על הפסוק "כל פיל מעופף יודע קרוא וכתוב; מכאן שיש פיל מעופף היודע קרוא וכתוב").
שלילת כמתים
כבר למדנו כיצד לשלול פסוק שבו הפעולה האחרונה היא אחד הקשרים. כדי לשלול פסוק שבו הפעולה האחרונה היא כמת מפעילים שתי הבחנות פשוטות, שנציג כדוגמאות:
- "לא כל תפוח הוא צהוב" שקול לכך ש"קיים תפוח שאינו צהוב".
- "לא קיים תפוח צהוב" שקול לכך ש"כל תפוח אינו צהוב".
כלומר, לכל פרדיקט P,
-
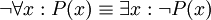 , וכך גם
, וכך גם -
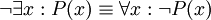 .
.
אפשר "לחסוך" ולהשתמש רק באחד משני הכמתים:
-
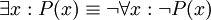 ("קיים סוס שחור" = "אין זה נכון שכל הסוסים אינם שחורים").
("קיים סוס שחור" = "אין זה נכון שכל הסוסים אינם שחורים").
באופן הזה אפשר להחליף כל מופע של הכמת "קיים" במופע אחד של הכמת "לכל"; כמובן, גם ההיפך אפשרי:
-
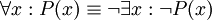 ("כל הסוסים שחורים" = "אין אף סוס שאינו שחור").
("כל הסוסים שחורים" = "אין אף סוס שאינו שחור").
בפועל, שני הכמתים נמצאים בשימוש מתמטי תמידי.
תרגיל. סדרה היא התאמה של מספר ממשי לכל מספר טבעי: 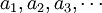 . מספר ממשי L הוא הגבול של הסדרה, אם לכל מספר חיובי שנבחר, יש מקום בסדרה שממנו והלאה מרחק האברים בסדרה מ-L קטן מן המספר האמור. הצרן את הטענות הבאות:
. מספר ממשי L הוא הגבול של הסדרה, אם לכל מספר חיובי שנבחר, יש מקום בסדרה שממנו והלאה מרחק האברים בסדרה מ-L קטן מן המספר האמור. הצרן את הטענות הבאות:
- "0 הוא הגבול של הסדרה
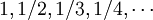 ".
". - "לסדרה
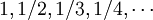 קיים גבול".
קיים גבול". - "L איננו הגבול של הסדרה
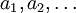 ".
". - "לסדרה
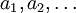 לא קיים גבול".
לא קיים גבול". - "אם יש לסדרה
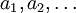 גבול, אז הוא יחיד".
גבול, אז הוא יחיד".
תרגיל. הפונקציה 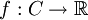 רציפה בנקודה x אם לכל
רציפה בנקודה x אם לכל 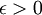 , קיים
, קיים 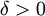 כך שאם
כך שאם 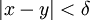 (עבור y בקטע) אז
(עבור y בקטע) אז 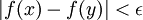 . הפונקציה רציפה בקטע C אם היא רציפה בכל הנקודות x הנמצאות בקטע. הצרן את הטענות הבאות:
. הפונקציה רציפה בקטע C אם היא רציפה בכל הנקודות x הנמצאות בקטע. הצרן את הטענות הבאות:
- הפונקציה
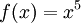 רציפה בקטע [0,1].
רציפה בקטע [0,1]. - הפונקציה
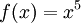 אינה רציפה בנקודה x=0.
אינה רציפה בנקודה x=0. - הפונקציה f רציפה בנקודה x אם ורק אם לכל סדרה
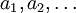 המתכנסת ל-x, הסדרה
המתכנסת ל-x, הסדרה 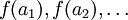 מתכנסת לערך
מתכנסת לערך 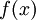 .
.
תרגיל. הפונקציה 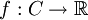 רציפה במידה שווה בקטע C אם לכל
רציפה במידה שווה בקטע C אם לכל 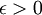 , קיים
, קיים 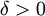 כך שלכל x,y בקטע, אם
כך שלכל x,y בקטע, אם 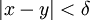 אז
אז 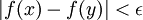 . הצרן את הטענות הבאות:
. הצרן את הטענות הבאות:
- הפונקציה
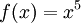 רציפה במידה שווה בקטע [0,1].
רציפה במידה שווה בקטע [0,1]. - הפונקציה
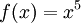 אינה רציפה במידה שווה בקטע [0,1].
אינה רציפה במידה שווה בקטע [0,1]. - אם הפונקציה f רציפה במידה שווה בקטע C, אז היא רציפה בכל נקודה שלו.
הגדרות
הגדרות הן אחד הדברים המיותרים ביותר במתמטיקה, משום שהגדרה אינה נושאת שום תוכן משל עצמה: כל מה שהיא עושה הוא להחליף תכונה או מצבור של תכונות במונח קצר וייחודי. מאידך, הגדרות הן אחד הדברים החיוניים ביותר במתמטיקה: הן מחליפות מושגים בסיסיים ביותר, בהדרגה, במושגים מורכבים יותר, שאפשר להבין את המשמעות שלהן כל אחת לעצמה, ולו היינו פורשים אותן ויורדים בכל פעם אל המושגים הבסיסיים ביותר, הטענות היו מגיעות לאורך שקשה לתפוס.
דוגמא. באי שבו גדלים עצי קוקוס, חיים להם קופים ארוכי זנב. קוף x יכול להיות בעלים של אגוז קוקוס a (זהו פרדיקט). שני קופים הם חברים אם כל אחד מהם חולק לפחות מחצית מאגוזי הקוקוס שלו עם הקוף השני. קבוצה של קופים היא משפחה, אם לכל אגוז קוקוס השייך לאחד הקופים במשפחה, יש קוף אחר במשפחה שהוא בעלים של אותו אגוז. שתי משפחות הן חברות אם יש קוף במשפחה האחת שהוא חבר של קוף מן המשפחה האחרת. קבוצה של משפחות היא שבט, אם לכל שתי משפחות בשבט יש משפחה בשבט שהיא חברה של שתיהן. קוף הוא מנהיג של שבט, אם יש לו אגוז משותף עם כל קוף בשבט, פרט לקופים במשפחה אחת לכל היותר. האי מסודר אם לכל שבט יש מנהיג יחיד. נסו להצרין את המושג "האי מסודר" ישירות מתוך הפרדיקט.
הסיפור הזה מדגים כמה תופעות שכיחות. הגדרנו מושגים כמו "משפחה" ו"שבט", ונתנו להם משמעות חדשה, המתעלמת מן המשמעות המקובלת. מתמטיקאים עושים דברים כאלה כל הזמן (למושגים הבאים יש משמעות מתמטית טכנית ומוגדרת היטב: חוג, שדה, מרחב, איבר, קבוצה, קשת, צביעה, חבורה, חבורה חופשית, מלה, שפה). השתמשנו באותה מלה (חברות) כדי לציין שני דברים שונים, אבל קרובים זה לזה: חברות של קופים וחברות של משפחות; גם זו תופעה נפוצה ביותר. בנינו כל הגדרה תוך שימוש חופשי בהגדרות קודמות: מרגע שהמושג הוגדר, הוא נכנס לשפת הדיבור, וקשה - איננו מנסים - להסתדר בלעדיו.
מכל הסיבות האלה, חשוב מאד לזכור ולהבין כל הגדרה שאתם נתקלים בה. לכל ההגדרות יש מבנה אחיד: דבר מסויים נקרא בשם מסויים, אם הוא מקיים תכונה מסויימת. לדוגמא, קבוצה של קופים היא משפחה אם היא מקיימת תכונה מסויימת; ההגדרה אינה יכולה לחול על מה שאיננו קבוצה של קופים; אין משמעות לשאלה "האם אגוז קוקוס זה הוא משפחה", משום שהגדרנו מהי משפחה רק עבור קבוצות של קופים. בהמשך הדרך נוכל גם להגדיר מתי קבוצת אגוזי קוקוס היא משפחה - ואז, כאשר נתון ש-A היא משפחה, יהיה עלינו להבין מן ההקשר האם מדובר בקבוצה של קופים (שהיא משפחה), או בקבוצה של אגוזי קוקוס.
כדי להבין הגדרה, תצטרכו לדמיין איזו תכונה היא אמורה לתפוס. בשלב ראשון כדאי לבדוק את ההגדרה על מקרים קיצוניים: האם קוף יכול להיות חבר של עצמו? (כן; כל קוף הוא חבר של עצמו). מיהם החברים של קוף שאין לו אגוזי קוקוס? (כל הקופים שאין להם אגוזי קוקוס, ורק הם). האם יכולה להיות משפחה שיש בה רק קוף אחד? (לא). וכן הלאה.
לפעמים הגדרה דורשת עבודת הכנה. יכולנו להגדיר, עבור שבט של קופים, ש"מלך השבט הוא הקוף שיש לו אגוז משותף עם כל קוף בשבט", אבל השימוש בהא-הידיעה רומז שאכן קיים לכל שבט מלך (יחיד), וזה בכלל לא ברור. הגדרה כזו אינה תקפה, עד שנוכיח את הקיום והיחידות של המלך. באי מסודר, המושג "מנהיג השבט" מוגדר כראוי, לא משום שהתאמצנו להוכיח את קיומו, אלא משום שכך הגדרנו מהו אי מסודר; גם זה תעלול מתמטי שכיח למדי.
הוכחות
עד כאן עסקנו במבנה הצורני של טענות: בתרגום לשפה פורמלית, בפסוקים שקולים וכדומה. עיקר העניין במתמטיקה אינו בטענות סתם, אלא בטענות נכונות, ולא בטענות נכונות סתם, אלא באלו שאפשר להוכיח. אם כך, עלינו ללמוד להוכיח טענות: כיצד מוכיחים, כיצד כותבים הוכחה, כיצד בודקים הוכחה, ומהן השגיאות הנפוצות שמהן יש להמנע. התשובה שניתן כאן לשאלות האלה היא חלקית ועל קצה המזלג, ותגע ברעיונות הבסיסיים בלבד. ככל שתלמדו מושגים מתקדמים ותורות חדשות, תלמדו גם טכניקות מתקדמות להוכחת טענות.
פסוק שיש לו הוכחה מתמטית נקרא משפט. המשפטים מבוססים על משפטים קודמים להם וכן הלאה, עד שמגיעים אל האקסיומות היסודיות. בכל תורה מתמטית יש אקסיומות (למעט הלוגיקה הפסוקית, שבה אין בהן צורך). חלק מן הפסוקים האמיתיים שפגשנו קודם לכן נחשבים לאקסיומות בכל מערכת מתמטית.
מודוס פוננס
הוכחה פורמלית של פסוק P היא רצף של פסוקים 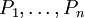 שכל אחד מהם הוא או אקסיומה, או שאפשר לגזור אותו באופן פורמלי מפסוקים קודמים: אם
שכל אחד מהם הוא או אקסיומה, או שאפשר לגזור אותו באופן פורמלי מפסוקים קודמים: אם 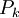 אינו אקסיומה, צריכים להיות קיימים
אינו אקסיומה, צריכים להיות קיימים 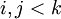 כך ש-
כך ש- 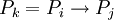 .
.
הגזירה מתבססת כאן על הכלל הלוגי היסודי הנקרא מודוס פוננס: מ- 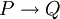 ו-
ו- 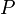 אפשר לגזור (כלומר להסיק את)
אפשר לגזור (כלומר להסיק את) 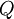 .
.
בלימודי המתמטיקה תפגשו הוכחות פורמליות לעתים נדירות ביותר. בדרך כלל מסתפקים בהוכחה מדוקדקת שאמנם אינה פורמלית, אבל אפשר לתרגם אותה להוכחה פורמלית. בכל שלב מהותי של ההוכחה תוכלו לזהות שמגיעים אל המסקנה מתוך שתי עובדות שהוכחו קודם לכן: ההנחה, והטענה שההנחה גוררת את המסקנה.
שימו לב. מהטענה 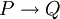 לא נובע P, ולא נובע Q, אלא רק שאם P אז Q. תנו דוגמא מפורשת לכך.
לא נובע P, ולא נובע Q, אלא רק שאם P אז Q. תנו דוגמא מפורשת לכך.
תרגיל. נניח שהמשפט הבא הוא אמיתי: "כאשר אני בכושר אני מסוגל לרוץ 10 קילומטר".
- נניח עוד כי "כעת איני בכושר" האם אני מסוגל לרוץ 10 קילומטר? אם לא, הוכח (באמצעות הצרנה).
- נניח שאיני מסוגל לרוץ 10 קילומטר, האם אני בכושר? הוכח.
- נניח שאני מסוגל לרוץ 10 קילומטר, האם אני בכושר? הוכח.
"בלי הגבלת הכלליות"
דוגמא. בין המספרים השלמים מוגדרת פעולת כפל, ומוגדר יחס של חלוקה: 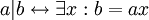 . מספר p, שאינו אפס ואינו מחלק את 1, הוא ראשוני אם
. מספר p, שאינו אפס ואינו מחלק את 1, הוא ראשוני אם 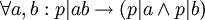 . מספר p, שאינו אפס ואינו מחלק את 1, הוא אי-פריק אם
. מספר p, שאינו אפס ואינו מחלק את 1, הוא אי-פריק אם 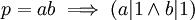 . נוכיח שכל מספר ראשוני הוא אי-פריק: יהי p מספר ראשוני. כדי להוכיח שהוא אי-פריק, עלינו להראות שאם p=ab אז a|1 או b|1. נניח, אם כך, ש- p=ab. מכיוון ש- ab=p*1, p|ab ומכיוון ש-p ראשוני, בלי הגבלת הכלליות, אפשר להניח ש- p|a. אבל אז קיים x כך ש- a=px=abx, ומכיוון ש-
. נוכיח שכל מספר ראשוני הוא אי-פריק: יהי p מספר ראשוני. כדי להוכיח שהוא אי-פריק, עלינו להראות שאם p=ab אז a|1 או b|1. נניח, אם כך, ש- p=ab. מכיוון ש- ab=p*1, p|ab ומכיוון ש-p ראשוני, בלי הגבלת הכלליות, אפשר להניח ש- p|a. אבל אז קיים x כך ש- a=px=abx, ומכיוון ש-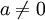 (אחרת p=0), אפשר לצמצם ולקבל bx=1, ומכאן b|1.
(אחרת p=0), אפשר לצמצם ולקבל bx=1, ומכאן b|1.
במלים "בלי הגבלת הכלליות" מותר להשתמש כשמבצעים הנחה שאינה מתחייבת מן הנתונים (במקרה שלנו, הנחנו ש-p|a, בעוד שכל מה שידוע לנו הוא ש-p|a או p|b; אולי דווקא p|b, ואז לא ידוע האם p|a?), ובכל זאת ברור שהיא מכסה את כל האפשרויות. במקרה שלנו אפשר היה לנסח כך: ראינו ש-p|ab, ומכיוון ש-p ראשוני, הוא מחלק את אחד הגורמים; אם הוא מחלק את b, נחליף את שמות הגורמים, וכך אפשר יהיה להניח שבכל מקרה p|a.
הוכחת טענות מכומתות
פסוק ללא כמתים אפשר להוכיח באמצעות טבלת אמת. כל הפסוקים מסוג זה נחשבים לאמיתות טריוויאליות, ולכן הם נמצאים בשכבה הראשונה של מאגר האקסיומות. את ההוכחה של פסוקים מורכבים יותר אפשר לתפוס כמשחק בין שני צדדים: ה"מוכיח", וה"יריב".
- כדי להוכיח טענה מהסוג
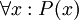 , על המוכיח להראות את אמיתות הטענה
, על המוכיח להראות את אמיתות הטענה 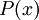 , וזאת לכל x *שבחר היריב*. היריב עשוי לבחור x שעבורו הוכחת הטענה קשה יותר. למוכיח אסור לבחור את x בעצמו, משום שהוא צריך להוכיח את הטענה לכל x.
, וזאת לכל x *שבחר היריב*. היריב עשוי לבחור x שעבורו הוכחת הטענה קשה יותר. למוכיח אסור לבחור את x בעצמו, משום שהוא צריך להוכיח את הטענה לכל x. - כדי להוכיח טענה מהסוג
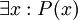 , המוכיח צריך להראות את אמיתות הטענה
, המוכיח צריך להראות את אמיתות הטענה 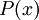 עבור x כלשהו. הדרך הקלה והבטוחה ביותר לעשות זאת היא *להצביע* על x שעבורו הטענה נכונה; זוהי הוכחה קונסטרוקטיבית. יש גם הוכחות לא קונסטרוקטיביות, אבל בשלבי הלימודים הראשונים תתקלו בהן רק לעתים רחוקות.
עבור x כלשהו. הדרך הקלה והבטוחה ביותר לעשות זאת היא *להצביע* על x שעבורו הטענה נכונה; זוהי הוכחה קונסטרוקטיבית. יש גם הוכחות לא קונסטרוקטיביות, אבל בשלבי הלימודים הראשונים תתקלו בהן רק לעתים רחוקות.
בדרך כלל המשחק כולל יותר משלב אחד. למשל, כדי להוכיח "לכל x חיובי קיים y חיובי הקטן ממנו", עלינו לאפשר ליריב לבחור x כרצונו; אחר-כך עלינו להראות שקיים y הקטן מן ה-x הזה, וזאת נעשה על-ידי בחירת y מתאים (למשל: 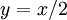 ). אפשר לכתוב זאת כך:
). אפשר לכתוב זאת כך:
- יהי
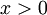 (היריב בוחר x כרצונו). נבחר
(היריב בוחר x כרצונו). נבחר 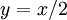 , ואז
, ואז 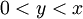 (כאן אנו מראים שעבור y שבחרנו, הטענה אכן מתקיימת).
(כאן אנו מראים שעבור y שבחרנו, הטענה אכן מתקיימת).
נזכיר שהסדרה 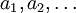 מתכנסת לגבול L אם
מתכנסת לגבול L אם
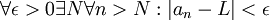 ; אכן, ההגדרה של מושג יסודי זה באנליזה כוללת שלושה כמתים. כדי לומר "הסדרה מתכנסת" (=יש מספר L שהוא הגבול שלה) נחוצים ארבעה כמתים. כדי להוכיח שסדרה נתונה מתכנסת, עלינו להצביע על ערכו הנכון של L; לתת ליריב לבחור את
; אכן, ההגדרה של מושג יסודי זה באנליזה כוללת שלושה כמתים. כדי לומר "הסדרה מתכנסת" (=יש מספר L שהוא הגבול שלה) נחוצים ארבעה כמתים. כדי להוכיח שסדרה נתונה מתכנסת, עלינו להצביע על ערכו הנכון של L; לתת ליריב לבחור את 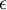 ; לבחור N, ולהראות שלכל n>N שיבחר היריב, מתקיים
; לבחור N, ולהראות שלכל n>N שיבחר היריב, מתקיים 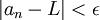 .
תרגיל. תאר את מהלך המשחק המוכיח שסדרה מסויימת אינה מתכנסת.
.
תרגיל. תאר את מהלך המשחק המוכיח שסדרה מסויימת אינה מתכנסת.
להלן כמה טכניקות הוכחה שכיחות.
- "מספיק להוכיח ש-": לפעמים הדרך הקצרה ביותר להוכיח טענה מסויימת היא הוכחת טענה חזקה יותר. זהו שימוש ישיר במודוס פוננס: במקום להוכיח את Q, אנו מוכיחים את P, כאשר הטענה
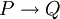 ידועה מראש. למשל, כדי להוכיח "קיים מספר ראשוני הגדול מ-
ידועה מראש. למשל, כדי להוכיח "קיים מספר ראשוני הגדול מ-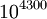 ", מספיק להוכיח שקיימים אינסוף ראשוניים.
", מספיק להוכיח שקיימים אינסוף ראשוניים. - הוכחה בדרך השלילה מבוססת על הטאוטולוגיה
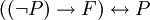 . כדי להוכיח את P, אנו מניחים את לא-P, ומראים שההנחה הזו מביאה לסתירה.
. כדי להוכיח את P, אנו מניחים את לא-P, ומראים שההנחה הזו מביאה לסתירה.
הפרכה של טענה אינה אלא הוכחה שהטענה אינה נכונה. הדוגמא החשובה ביותר היא הפרכה על-ידי דוגמא נגדית:
- כדי להפריך את הטענה
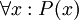 , יש להראות שקיים x שעבורו הטענה
, יש להראות שקיים x שעבורו הטענה 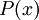 אינה נכונה. גם כאן, הדרך השכיחה ביותר היא להצביע על ערך מסויים של x שעבורו הטענה אינה נכונה.
אינה נכונה. גם כאן, הדרך השכיחה ביותר היא להצביע על ערך מסויים של x שעבורו הטענה אינה נכונה.
תרגילים.
- השתמש בפרדיקט
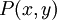 (אדם x חובב חיות מסוג y) כדי להצרין את הטענה "כל אדם החובב חיות, חובב לפחות שני סוגים שלהן". מה יש לעשות כדי להוכיח טענה כזו? מה יש לעשות כדי להפריך אותה?
(אדם x חובב חיות מסוג y) כדי להצרין את הטענה "כל אדם החובב חיות, חובב לפחות שני סוגים שלהן". מה יש לעשות כדי להוכיח טענה כזו? מה יש לעשות כדי להפריך אותה? - מרחב הוא קומפקטי אם לכל כיסוי פתוח שלו, יש תת-כיסוי סופי. לצורך העניין אין זה חשוב מהו כיסוי פתוח של מרחב, מהו תת-כיסוי, ומתי תת-כיסוי הוא סופי; נעיר רק שכל תת-כיסוי הוא בעצמו כיסוי (אם תרצו, אתם יכולים להצרין את כל הנתונים האלה). קבע אלו מההגדרות הבאות שקולות:
- המרחב K הוא קומפקטי אם ורק אם יש לו כיסוי סופי.
- המרחב K הוא קומפקטי אם ורק אם יש לו כיסוי פתוח שיש לו תת-כיסוי סופי.
- המרחב K אינו קומפקטי אם ורק אם יש לו כיסוי פתוח שאין לו תת-כיסוי סופי.
- גם כאשר ההגדרה באחד הסעיפים הקודמים אינה שקולה מבחינה לוגית, על-פי הפרדיקטים שניסחתם; לכאורה יתכן שההגדרות כן שקולות, משום שיש תכונות נוספות של כיסויים פתוחים שלא לקחתם בחשבון. אלו תכונות של כיסויים פתוחים יספיקו כדי לקבוע בכל מקרה שההגדרות באמת אינן שקולות?
שגיאות נפוצות
שגיאות בהוכחה נדירות למדי באולמות ההרצאה, אבל עד שמתרגלים לחומר ולומדים אותו היטב, הן די שכיחות מחוץ להם. היכרות טובה עם שגיאות נפוצות יכולה לעזור לכם להמנע מהן.
אחת השגיאות הנפוצות היא החלפת סדר כמתים. יש הבדל עצום בין "לכל סיר יש מכסה המתאים לו", לבין "יש מכסה המתאים לכל הסירים". הצרינו את שתי הטענות, וקבעו איזו מהן גוררת את השניה.
שגיאה פופולרית נוספת היא הנחת המבוקש. צריך להוכיח שלכל נחש יש ארבע שיניים. יהי x נחש. בתחילת השאלה כתוב במפורש - "לכל נחש יש ארבע שיניים"; לכן יש ל-x ארבע שיניים, מש"ל.
שגיאה נוספת, הנובעת מחוסר תשומת לב (או ממצוקה פנים-מבחנית) היא שימוש ב"טאוטולוגיות" שגויות.
- כל החתולים צהובים. רוצים להראות ש-c חתול. לשם כך מראים שהוא צהוב.
חומר נוסף
הצרנה
מילולית
נביט בשלושה משפטים:
- השמש זורחת אם ורק אם כל התרנגולים קוראים
- כאשר השמש זורחת, כל התרנגולים קוראים
- כאשר התרנגול קוקי קורא, השמש זורחת
האם המשפט הראשון נובע בהכרח משני הראשונים? אם לא הבא דוגמא נגדית - כלומר, נניח ומשפטים 2 ו3 הינם אמת, האם יש מצב של זריחת השמש וקריאת התרנגולים שסותרת את המשפט הראשון?
מתמטית
- הטור
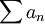 מתכנס בהחלט אם"ם לכל סדרה חסומה
מתכנס בהחלט אם"ם לכל סדרה חסומה 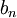 מתקיים ש
מתקיים ש  מתכנס
מתכנס - אם הטור
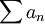 מתכנס בהחלט אזי לכל סדרה חסומה
מתכנס בהחלט אזי לכל סדרה חסומה 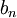 מתקיים ש
מתקיים ש  מתכנס
מתכנס - קיימת סדרה חסומה
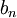 כך שהעובדה ש
כך שהעובדה ש מתכנס גוררת שהטור
מתכנס גוררת שהטור 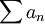 מתכנס בהחלט
מתכנס בהחלט
התרגיל המתמטי הזה שקול לתרגיל המילולי לעיל:
- "השמש זורחת" = "הטור
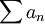 מתכנס בהחלט"
מתכנס בהחלט" - "תרנול" = "סדרה חסומה"
- "תרנגול קורא" = "סדרה חסומה
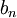 כך ש
כך ש  מתכנס"
מתכנס"