88-101 חשיבה מתמטית
הסדנא בחשיבה מתמטית מרכיבה את חלקו הראשון של הקורס מתמטיקה בדידה, ומטפלת בעקרונות היסוד של החשיבה המתמטית: כתיבה מדוייקת, לוגיקה פורמלית והוכחות מסודרות.
תוכן עניינים
הצרנה
הצרנה היא תרגום של פסוק או טיעון יומיומי או מתמטי לשפה לוגית מדוייקת, על-פי צורתו, תוך התעלמות מתוכנו. לאחר שהפסוק תורגם, אפשר להפעיל עליו כלים לוגיים סטנדרטיים על-מנת לבחון אותו, להעביר אותו לצורה שקולה, לעמת אותו עם פסוקים אחרים, וכדומה.
דוגמא. אם לא תגמור מהצלחת, יבוא שוטר. כדי לטפל בפסוק כזה, עלינו להגדיר שני אטומים: A="תגמור מהצלחת", B="יבוא שוטר". הפסוק קובע "אם לא A אז B". כך אפשר לראות מיד שיש לו אותו מבנה לוגי, אותה צורה, כמו לפסוק הבא: דוגמא. אם לא נכלכל את צעדינו בתבונה, נמצא את עצמנו מול שוקת שבורה. (אם לא A אז B, כאשר A="נכלכל את צעדינו בתבונה" ו-B="נמצא את עצמנו מול שוקת שבורה").
הדוגמאות יכולות להיות מסובכות בהרבה: דוגמא. ... (כלומר, עבור הביטויים המתאימים עבור A,B,C,D: (אם A וגם B אז C או D), וגם (אם לא A וגם C אז לא B)).
((הצרנה של ביטויים כמו "ולכן", "אבל", "ובכל זאת")).
ערך אמת
ערך אמת הוא אחת משתי האפשרויות - אמת או שקר, שמסמנים לשם הקיצור T ו-F (מ-True ו-False, כמובן). בתאור מדוייק ומכריע של העולם, כל אטום (מפורט מספיק) מקבל ערך אמת. או שתגמור מהצלחת, או שלא. או שיבוא שוטר, או שלא. אם תגמור מהצלחת, אז ערך האמת של הפסוק "תגמור מהצלחת" הוא T, ואחרת, הוא F. זו הדרך לחבר את המציאות, את תמונת העולם, עם הפסוקים הלוגיים הפורמליים.
כאשר משייכים לכל אטום של פסוק לוגי ערך אמת, אפשר לחשב את ערך האמת של הפסוק עצמו. לשם כך יש להכיר את הקשרים הלוגיים הבסיסיים.
הצרנת תכונות
הצרן את הפסוקים הבאים: ... (דוגמאות מהחיים. דוגמאות מהחיים המתמטיים).
פסוקים וקשרים
וגם הוא קשר לוגי: אפשר לומר משפטים כמו "התפוח הזה אדום, וגם הצלחת ירוקה", שההצרנה שלהם היא במבנה "A וגם B". אי אפשר לומר "התפוח הזה אדום וגם", משום ש"וגם" הוא קשר בינארי - הוא מחבר שני אטומים. ערך האמת של הפסוק "A וגם B" הוא T, רק כאשר גם A וגם B הם T. בכל מקרה אחר, ערך האמת הוא F.
דוגמא. כשפוליטיקאי מבטיח "לא נעלה מסים וגם נגדיל את ההוצאה לחינוך" (שצורתו "(לא A) וגם B"), הוא יצטרך לקיים שתי הבטחות: גם לא A, וגם B.
כבר פגשנו את קשר השלילה, לא, שהוא הקשר האונארי היחיד. הפסוק המתקבל משלילת A הוא, כמובן, "לא A"; ערך האמת שלו הפוך לזה של A: אם "יבוא שוטר" הוא פסוק אמיתי, אז "לא יבוא שוטר" הוא פסוק שקרי, ולהיפך.
קשר נוסף הוא או: גם הוא קשר בינארי, המאפשר לבנות את הפסוק "A או B". פסוק כזה מקבל ערך אמת T אם אחת ההצהרות קיבלה ערך אמת T, או שתיהן.
דוגמא. כשפוליטיקאי מבטיח "לא נעלה מסים, או שנגדיל את ההוצאה לחינוך" (שצורתו "(לא A) או B"), הוא יוכל להסתפק בקיום אחת ההבטחות.
הקשר אם-אז בונה משפטים כמו "אם נגדיל את ההוצאה לחינוך, נעלה מסים": "אם A אז B". אם ערך האמת של A הוא T, אז ערך האמת של "אם A אז B" שווה לערך האמת של B: אם מבטיחים, ההצהרה "אם הבטחתי אז אקיים" נכונה אם אקיים, ולא נכונה אם לא אקיים. לעומת זאת, אם לא הבטחתי, ההצהרה נכונה בכל מקרה: כשערך האמת של A הוא F, ערך האמת של "אם A אז B" הוא T בלי קשר לערך האמת של B. זהו הסכם חשוב, גם אם קצת קשה לקבל אותו בתחילה. נראה עוד כמה דוגמאות.
- "אם לסבתא היו גלגלים היא היתה אוטובוס". זהו פסוק מהצורה "אם A אז B", כאשר A="לסבתא יש גלגלים", ו-B="סבתא היא אוטובוס". בהנחה ששתי הטענות שקריות, הפסוק עצמו הוא נכון: אם היו לסבתא גלגלים אז היא היתה אוטובוס, אבל אין לה, כך שזה בכלל לא חשוב אם היא אוטובוס או לא; הפסוק אמיתי.
תרגיל. בדוק שאם ערך האמת של B הוא T, אז ערך האמת של "אם A אז B" הוא תמיד T. קבע מתי ערך האמת של "אם A אז B" הוא T, אם ידוע שערך האמת של B הוא F.
דוגמא. הפסוק "אם יש עננים אז יורד גשם" אינו אמיתי, משום שיתכן שיהיו עננים בלי שירד גשם. לעומת זאת הפסוק "אם יורד גשם אז יש עננים" הוא אמיתי. את הפסוק השני, האמיתי, אפשר לנסח בצורות נוספות: "יש עננים אם יורד גשם" (מוכרחים להיות עננים אם יורד גשם), וגם "יורד גשם רק אם יש עננים" (כל אימת שיורד גשם, מוכרחים להיות עננים).
נסכם: הפסוקים "אם A אז B", "B אם A" ו"A רק אם B" אומרים אותו הדבר.
לכן, במקום להגיד "אם B אז A, וגם אם A אז B", אפשר לומר "A אם B, ו-A רק אם B", ובקיצור "A אם ורק אם B". זהו הקשר הבינארי האחרון שנציג בשם: אם ורק אם. ערך האמת של "A אם ורק אם B" הוא T בדיוק כאשר ערכי האמת של A ושל B שווים. דוגמא. משולש הוא ישר זווית ושווה שוקיים אם ורק אם יש לו שתי זוויות של 45 מעלות.
סימוני הקשרים
לקשרים הסטנדרטיים יש גם סימון סטנדרטי, שיש להכיר ולזכור.
- במקום "לא A" כותבים
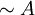 או
או 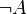 .
. - במקום "A וגם B" כותבים
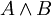 .
. - במקום "A או B" כותבים
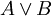 .
. - במקום "אם A אז B" כותבים
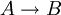 ; מותר גם
; מותר גם 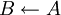 .
. - במקום "A אם ורק אם B" כותבים
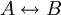 .
.
פסוקים מורכבים
את הקשרים שפגשנו (לא, וגם, או, אם-אז, אם-ורק-אם) אפשר להפעיל לא רק על אטומים, אלא גם על פסוקים.
דוגמא. אם אדם הוא מאושר אם ורק אם הוא לומד דברים חדשים, אז אדם שאינו לומד דברים חדשים אינו מאושר. ("אם (A אם ורק אם B), אז (אם לא B, אז לא A)").
עד כאן לא הגדרנו מהו "פסוק". פסוק הוא בסופו של דבר רצף של תווים, שכל אחד מהם הוא או אחד האטומים (מקובל להניח שעומדת לרשותנו אספקה אינסופית של אטומים), או אחד מסימני הקשרים, או אחד הסימנים המיוחדים "(" ו")" שתפקידם להבטיח קריאה חד-משמעית של הפסוק. לדוגמא, הפסוק 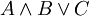 אינו ניתן לקריאה באופן ברור: אין לדעת האם הכוונה היא ל-
אינו ניתן לקריאה באופן ברור: אין לדעת האם הכוונה היא ל-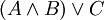 או ל-
או ל-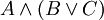 . (תרגיל: מצא ערכי אמת של A,B,C שיתנו ערכי אמת שונים לשני הפסוקים האחרונים). הכלל במקרה של ספק הוא פשוט: עדיף לבזבז מאה זוגות סוגריים מיותרים, מאשר להשמיט זוג סוגריים חיוני אחד.
. (תרגיל: מצא ערכי אמת של A,B,C שיתנו ערכי אמת שונים לשני הפסוקים האחרונים). הכלל במקרה של ספק הוא פשוט: עדיף לבזבז מאה זוגות סוגריים מיותרים, מאשר להשמיט זוג סוגריים חיוני אחד.
כמובן שלא כל רצף של סימנים הוא פסוק. "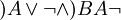 " אינו פסוק. אפשר להגדיר פסוקים "באינדוקציה על המבנה":
" אינו פסוק. אפשר להגדיר פסוקים "באינדוקציה על המבנה":
- כל פסוק הוא או אטום, או בצורה
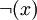 כאשר x הוא פסוק, או בצורה
כאשר x הוא פסוק, או בצורה 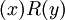 , כאשר R הוא אחד מסימני הקשרים הבינאריים, ו-x,y הם פסוקים.
, כאשר R הוא אחד מסימני הקשרים הבינאריים, ו-x,y הם פסוקים.
הגדרה זו היא אחת מאבני היסוד של הלוגיקה הפסוקית, המטפלת בפסוקים באופן פורמלי. תרגיל. הוכח, באינדוקציה על אורך הפסוק, שאפשר לבנות מכונה שתזהה האם רצף של תווים הוא פסוק או לא (הנח שהמכונה יודעת לזהות אטומים).
טבלאות אמת
טבלת אמת מאפשרת לטפל בפסוק על-ידי בחינת כל האפשרויות לערכי אמת של האטומים המעורבים בו. טכנית, אם בפסוק יש n אטומים, הטבלה מורכבת מ-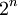 שורות, שבכל אחת מהן מקצים אפשרות אחרת לערכי האמת של האטומים. למשל, בטבלת האמת של
שורות, שבכל אחת מהן מקצים אפשרות אחרת לערכי האמת של האטומים. למשל, בטבלת האמת של 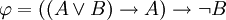 יש ארבע שורות, המתאימות לערכי האמת TT, TF, FT, FF עבור האטומים AB. בטבלה יש להוסיף גם את ערך האמת של כל תת-פסוק (במקרה דנן,
יש ארבע שורות, המתאימות לערכי האמת TT, TF, FT, FF עבור האטומים AB. בטבלה יש להוסיף גם את ערך האמת של כל תת-פסוק (במקרה דנן, 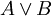 ו-
ו- 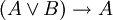 ), ובסופו של דבר את ערך האמת של הפסוק עצמו.
), ובסופו של דבר את ערך האמת של הפסוק עצמו.
פסוק שערך האמת שלו הוא תמיד T, לכל הצבה של ערכי אמת באטומים, נקרא טאוטולוגיה. פסוק שערך האמת שלו הוא תמיד F נקרא סתירה.
לטאוטולוגיות חשיבות מיוחדת בלוגיקה, משום שהם מבטאות אמת צורנית אוניברסלית, שאינה תלויה בהצבת ערכי האמת. (ראו גם [1]).
דוגמא. הפסוק 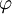 שהוזכר לעיל הוא טאוטולוגיה. הוא קובע שאם מההנחה "A או B" אפשר להסיק את A, אז B מוכרח להיות שקרי.
שהוזכר לעיל הוא טאוטולוגיה. הוא קובע שאם מההנחה "A או B" אפשר להסיק את A, אז B מוכרח להיות שקרי.
תרגיל. אם 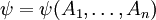 הוא פסוק טאוטולוגי התלוי באטומים
הוא פסוק טאוטולוגי התלוי באטומים 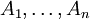 , אז כל פסוק המתקבל מהצבה של פסוקים כלשהם
, אז כל פסוק המתקבל מהצבה של פסוקים כלשהם 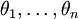 במקום האטומים (באופן עקבי), גם הוא טאוטולוגי.
במקום האטומים (באופן עקבי), גם הוא טאוטולוגי.
חשוב להכיר טאוטולוגיות בסיסיות, ועוד יותר חשוב לדעת כיצד בודקים האם פסוק הוא טאוטולוגי, ולזהות פסוקים שאינם טאוטולוגיות. דוגמאות. להלן כמה טאוטולוגיות שקל לבדוק:
-
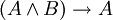 (כלומר, אם A וגם B, אז בפרט A);
(כלומר, אם A וגם B, אז בפרט A); -
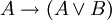 (אם A, אז בוודאי מתקיים A או B);
(אם A, אז בוודאי מתקיים A או B); -
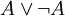 (זהו "כלל השלישי הנמנע": או שהתפוח אדום או שאינו אדום (כמובן, בתנאי שמגדירים היטב מתי תפוח הוא אדום));
(זהו "כלל השלישי הנמנע": או שהתפוח אדום או שאינו אדום (כמובן, בתנאי שמגדירים היטב מתי תפוח הוא אדום)); -
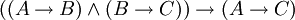 (אם מ-A נובע B ומ-B נובע C, אז מ-A נובע C).
(אם מ-A נובע B ומ-B נובע C, אז מ-A נובע C).
אפשר להמציא עוד טאוטולוגיות כהנה וכהנה. תרגיל. הסבר מדוע פסוק שמופיעים בו רק הקשרים הלוגיים "או" ו"וגם" אינו יכול להיות טאוטולוגיה.
הגדרתו של הקשר הלוגי "אם ורק אם" מובילה אותנו להגדרה שימושית:
הגדרה. הפסוקים 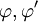 הם שקולים אם הפסוק
הם שקולים אם הפסוק 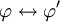 הוא טאוטולוגיה. במקרה כזה מסמנים
הוא טאוטולוגיה. במקרה כזה מסמנים 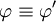 .
.
דוגמאות.
-
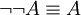
-
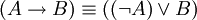 .
. -
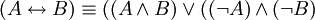 .
. -
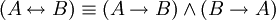 .
. -
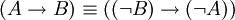 .
.
משפט. כל פסוק לוגי שקול לפסוק שבו מופיעים רק קשר השלילה והקשרים "או" ו"וגם".
חוקי דה-מורגן
חשוב לדעת לנסח במדוייק את השלילה של פסוק נתון. הדוגמאות הבסיסיות מסוג זה נקראות כללי דה-מורגן:
-
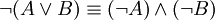 .
. -
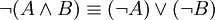 .
.
משפט. כל פסוק לוגי שקול להצבת האטומים 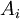 ושלילתם
ושלילתם 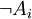 , בפסוק שבו מופיעים רק הקשרים "או" ו"וגם".
, בפסוק שבו מופיעים רק הקשרים "או" ו"וגם".
כמתים
(לכל, קיים, קיים יחיד, קיימים אינסוף) + כימות יחסי (קיים אפסילון גדול מאפס, לכל אפסילון גדול מאפס)
הוכחה
מודוס פוננס
סילוגיזם תקין ולא תקין
הוכחה בדרך השלילה, הפרכה על-ידי דוגמא נגדית.
שגיאות נפוצות
חומר נוסף
- בניסוי מפורסם בתורת ההחלטות, מציגים לנבדק ארבעה כרטיסים שבגבם הסימנים A, P, 2, 3. על כל כרטיס יש אות ומספר. אלו כרטיסים יש להפוך על-מנת לבדוק את הטענה "אם בצד אחד של הכרטיס יש אות ניקוד (AEIOU) אז בצידו האחר יש מספר זוגי?" רוב גדול של האנשים עונים שיש להפוך את הכרטיס הראשון והשלישי. מה התשובה הנכונה?
- דוגמא להמחיש ששקר גורר כל דבר; ילד הרואה כלבה נחמדה מבקש מההורים שלו גור כלבים. ההורים היודעים שהכלבה מסורסת מבטיחים לו "אם הכלבה תמליט, תקבל גור אחד".
כמתים
אפשר להיעזר בספר של ליניאל ופרנס לפרק זה.
לעתים מוכיחים טענה "לכל 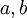 מתקיימת איזשהי תכונה
מתקיימת איזשהי תכונה 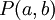 ". אחר כך בקורס, צריך להשתמש בכך ש
". אחר כך בקורס, צריך להשתמש בכך ש 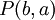 נכון. אבל לכאורה המשתנים לא כתובים כמו שהוכחנו. רעיון החלפת השמות של משתנים, במיוחד אם ממחזרים את אותם שמות בסדר אחר, הוא לא טריויאלי וצריך להציגו, בהדרגה:
נכון. אבל לכאורה המשתנים לא כתובים כמו שהוכחנו. רעיון החלפת השמות של משתנים, במיוחד אם ממחזרים את אותם שמות בסדר אחר, הוא לא טריויאלי וצריך להציגו, בהדרגה:
בטענה עם כמתים, תקפותה לא תשתנה אם נשנה את שמות המשתנים.
תקפותה לא תשתנה גם אם נחליף את שמות המשתנים זה בזה.
דוגמא נוספת מאותו סוג: תהי 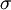 תמורה על
תמורה על 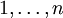 ונניח שלכל
ונניח שלכל 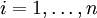 , יש ל
, יש ל 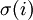 תכונה מסויימת. אזי אפשר, לכל
תכונה מסויימת. אזי אפשר, לכל 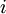 , להציב את
, להציב את 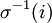 ולהסיק שלכל
ולהסיק שלכל 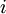 יש את התכונה הזו.
יש את התכונה הזו.
(זו רק הכוונה כללית, ההצגה טעונה שיפור, וגם כדאי להביא דוגמאות קונקרטיות.)
- בנושא אינדקסים ושמות משתנים - הוכחה כי מטריצה כפול המצורפת לה (adj) שווה למטריצת היחידה כפול הדטרמיננטה. ניתן להניח את הנוסחא של פיתוח לפי שורה, נוסחאת הכפל, ולומר שהדטרמיננטה של מטריצה בעלת שתי שורות זהות שווה לאפס. התלמידים צריכים להבין מדוע כל איבר במכפלה שאינו על האלכסון שווה לדטרמיננטה של מטריצה בעלת שתי שורות זהות.
שלילה
- שלילת הגדרות מקורסים שונים, כאשר הבנת ההגדרות לאו דוקא הכרחית: גבול סדרה, גבול פונקציה לפי היינה/קושי, רציפות במ"ש, התכנסות במ"ש, סכום ישר, חח"ע, על, ת"ל, מטריצה סימטרית, הפיכה,...
- כאן יכולה להכנס גם הדוגמא הבאה, שאיני מלמד בקורס בדידה, משום שבקונקסט שלו היא סתם מבלבלת, אבל בקורס שכולו עוסק בחשיבה לוגית-מתמטית היא מתאימה מאד לדעתי:
הפרדוקס של ראסל (המשפחה 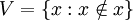 אינה קבוצה), ואחריו דיון:
אינה קבוצה), ואחריו דיון:
תהי  קבוצה כלשהי, ונגדיר
קבוצה כלשהי, ונגדיר 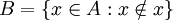 . האם
. האם  קבוצה? (כן).
קבוצה? (כן).
למה אי אפשר לקבל סתירה כמו בפרדוקס של ראסל?
הצרנה
תרגילים ודוגמאות אלו ילוו אותנו במהלך הסדנא:
אמביוולנטיות בין עברית לבין מתמטיקה
- נניח ויש קופסא המכילה 3 כדורים אותם נחלק בין 3 אנשים. אדם א' מציץ בקופסא ואומר "לא יכול להיות שמישהו יקבל כדור ירוק". אדם ב' אינו מסתכל בקופסא ואומר "יכול להיות שמישהו יקבל כדור ירוק". שניהם צודקים מכיוון שהמושג "יכול להיות", בדבריו של אדם ב', בעצם מופיע במשמעות של "לא הוכחתי שזה בלתי אפשרי", שזו עובדה חסרת משמעות מתמטית.
- מורה אומרת לתלמידיה "שבוע הבא יהיה לכם בוחן, כך שבערב לפניו לא תדעו בוודאות על קיום הבוחן למחרת". לכאורה משפט זה יוצר סתירה לוגית כיוון שאם הבוחן ביום האחרון בשבוע, והמורה דוברת אמת, התלמדים ידעו שהבוחן יהיה למחרת, לכן המורה משקרת או שהבוחן לא ביום האחרון. כן הלאה, אם המורה דוברת אמת הבוחן לא ביום הלפני אחרון והלפני לפני אחרון, ולא יכול להיות בוחן בכלל. לכן אם המורה דוברת אמת, הרי היא משקרת. לעומת זאת, אם הבוחן יהיה ביום שלישי, התלמידים לא ידעו על כך ולכן המורה דברה אמת - סתירה. הסתירה נובעת מחוסר היכולת להגדיר מתמטית את המושג "ידעו", שכן התלמידים לא יכולים "לדעת" שהמורה אומרת אמת, ולכן לא יכולים ל"דעת" שהבוחן יהיה ביום חמישי.
- שקילות משפטים בנוסחים שונים - "ערן לובש חולצה סגולה אם הוא לובש מכנס שחור", "כאשר ערן לובש מכנס שחור אז הוא לובש חולצה סגולה", "יחד עם מכנס שחור, ערן לובש חולצה סגולה בלבד",...
- חלוקת משפטים בנוסחים שונים לקבוצות שקילות - (המשפטים לעיל), "ערן לובש מכנס שחור רק כאשר הוא לובש חולצה סגולה", "ערן לובש חולצה סגולה אם ורק אם הוא לובש מכנס שחור", "לא רק שערן לובש תמיד חולצה סגולה כאשר הוא לובש מכנס שחור, הוא לעולם לא הולך עם חולצה סגולה ללא המכנס השחור",...
ההבדל בין 'אם' לבין 'אם ורק אם'
ראו הערה בדף השיחה לגבי השימוש ב"אם" במתמטיקה. בועז
- "שמוליק נמצא בביתו אם רכבו נמצא בחנייה". כלומר, כאשר אנו רואים את הרכב בחנייה אנו יכולים להסיק ששמוליק נמצא בביתו. אולם, אילו הרכב אינו בחנייה אנו לא יודעים היכן שמוליק - ייתכן ובנו לקח את הרכב ושמוליק נשאר בביתו. "שמוליק נמצא בביתו אם ורק אם רכבו נמצא בחנייה" ממשפט זה ניתן להסיק את שני הכיוונים - אם אנו צופים ברכב בחנייה וודאי שמוליק בביתו, ואם הרכב אינו בחנייה שמוליק בוודאי נמצא בחוץ (אין לאף אחד אחר ביטוח על הרכב).
דוגמא
מילולית
נביט בשלושה משפטים:
- השמש זורחת אם ורק אם כל התרנגולים קוראים
- כאשר השמש זורחת, כל התרנגולים קוראים
- כאשר התרנגול קוקי קורא, השמש זורחת
האם המשפט הראשון נובע בהכרח משני הראשונים? אם לא הבא דוגמא נגדית - כלומר, נניח ומשפטים 2 ו3 הינם אמת, האם יש מצב של זריחת השמש וקריאת התרנגולים שסותרת את המשפט הראשון?
מתמטית
- הטור
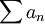 מתכנס בהחלט אם"ם לכל סדרה חסומה
מתכנס בהחלט אם"ם לכל סדרה חסומה 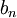 מתקיים ש
מתקיים ש  מתכנס
מתכנס - אם הטור
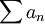 מתכנס בהחלט אזי לכל סדרה חסומה
מתכנס בהחלט אזי לכל סדרה חסומה 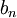 מתקיים ש
מתקיים ש  מתכנס
מתכנס - קיימת סדרה חסומה
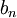 כך שהעובדה ש
כך שהעובדה ש מתכנס גוררת שהטור
מתכנס גוררת שהטור 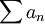 מתכנס בהחלט
מתכנס בהחלט
התרגיל המתמטי הזה שקול לתרגיל המילולי לעיל:
- "השמש זורחת" = "הטור
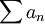 מתכנס בהחלט"
מתכנס בהחלט" - "תרנול" = "סדרה חסומה"
- "תרנגול קורא" = "סדרה חסומה
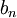 כך ש
כך ש  מתכנס"
מתכנס"
כתיבת הוכחה
הגדרות
נדבר על חשיבות ההגדרות בעת פתרון תרגיל וכתיבת הוכחה. היום התלמידים מנסים לפתור תרגילי הוכחה מבלי שידעו כלל את ההגדרה המדויקת (גבול, תלות לינארית וכדומה).
- מתורת הקבוצות: הכלה, חיתוך, איחוד,משלים, קבוצת החזקה. כתוב תנאים השקולים לכך שאיבר שייך/אינו שייך לחיתוך/איחוד.
- נגדיר קבוצה פתוחה בתור קבוצה שהמשלימה שלה סגורה. נניח וכל תתי הקבוצות פתוחות, כמה תתי קבוצות סגורות יש?
- נניח וfg חח"ע/על, האם בהכרח f,g חח"ע/על? כתוב הוכחה מדויקת.
דוגמאות
- הטיעון הפלאי "בלי הגבלת הכלליות": מתי מותר להשתמש בו ולמה, ומתי אינו תקף (דוגמאות).
(אני אישית משתדל להמנע מטיעון זה בשנה א', כי באמת תלמידים לא מבינים מתי הוא מותר. אבל כדאי שיכירו אותו, ואת מכשלותיו. בועז)
- נסתכל על תור המכיל אינסוף אנשים, החל מהראשון בתור והלאה. הוכח/הפרך: ניתן להוציא מהתור אנשים כך שנשארים אינסוף, והם מסודרים בצורה עולה או יורדת לפי הגובה. (נניח ואין מגבלות על גובה האדם)
מציאת שגיאות
אינדוקציה שגוייה
- נוכיח שכל הפרחים בעולם הינם מאותו צבע (אדום, לצורך העניין). הנחת האינדוקציה הינה "כל קבוצה המכילה בדיוק n פרחים, מכילה פרחים מאותו צבע בלבד". בדיקה עבור קבוצה המכילה פרח אחד בלבד עובדת. כעת, נניח כי יש לנו קבוצה בעלת n+1 פרחים. ניקח פרח אחד החוצה, n הפרחים הנותרים הינם מאותו הצבע. נחליף את הפרח שהוצאנו בפרח אחר, שוב הקבוצה תהיה באותו צבע ולכן סה"כ כל הפרחים הינם מאותו צבע. מצא את השגיאה.