88-101 חשיבה מתמטית - הגדרות והוכחות
זהו החלק השלישי (והאחרון) של המבוא לחשיבה מתמטית.
תוכן עניינים
הגדרות
הגדרות הן אחד הדברים המיותרים ביותר במתמטיקה, משום שהגדרה אינה נושאת שום תוכן משל עצמה: כל מה שהיא עושה הוא להחליף תכונה או מצבור של תכונות במונח קצר וייחודי. מאידך, הגדרות הן אחד הדברים החיוניים ביותר במתמטיקה: הן מחליפות מושגים בסיסיים ביותר, בהדרגה, במושגים מורכבים יותר, שאפשר להבין את המשמעות שלהן כל אחת לעצמה. לו היינו פורשים את ההגדרות ויורדים בכל פעם אל המושגים הבסיסיים ביותר, הטענות היו מגיעות לאורך שקשה לתפוס.
דוגמא. באי שבו גדלים עצי קוקוס, חיים להם קופים ארוכי זנב. קוף x יכול להיות בעלים של אגוז קוקוס a (זהו פרדיקט). לאגוז יכולים להיות כמה בעלים. שני קופים הם חברים אם כל אחד מהם חולק לפחות מחצית מאגוזי הקוקוס שלו עם הקוף השני. קבוצה של קופים היא משפחה, אם לכל אגוז קוקוס השייך לאחד הקופים בקבוצה, יש קוף אחר בקבוצה שהוא בעלים של אותו אגוז. שתי משפחות הן חברות אם יש קוף במשפחה האחת שהוא חבר של קוף מן המשפחה האחרת. קבוצה של משפחות היא שבט, אם לכל שתי משפחות בקבוצה יש משפחה בקבוצה שהיא חברה של שתיהן. קוף הוא מנהיג של שבט, אם יש לו אגוז משותף עם כל קוף בשבט, פרט לקופים במשפחה אחת לכל היותר. האי מסודר אם לכל שבט יש מנהיג יחיד. נסו להצרין את המושג "האי מסודר" ישירות מתוך הפרדיקט.
הסיפור הזה מדגים כמה תופעות שכיחות. הגדרנו מושגים כמו "משפחה" ו"שבט", ונתנו להם משמעות חדשה, המתעלמת מן המשמעות המקובלת. מתמטיקאים עושים דברים כאלה כל הזמן (למושגים הבאים יש משמעות מתמטית טכנית ומוגדרת היטב: עץ, יער, חוג, שדה, מרחב, איבר, קבוצה, קשת, צביעה, חבורה, חבורה חופשית, מלה, שפה). השתמשנו באותה מלה (חברות) כדי לציין שני דברים שונים, אבל קרובים זה לזה: חברות של קופים וחברות של משפחות; גם זו תופעה נפוצה ביותר. באותו אופן לא הצלחנו להמנע מהשימוש במלה "קבוצה" לתאור אוספים שונים בתכלית: של קופים, ושל קבוצות קופים. בנינו כל הגדרה תוך שימוש חופשי בהגדרות קודמות: מרגע שהמושג הוגדר, הוא נכנס לשפת הדיבור, וקשה - איננו מנסים - להסתדר בלעדיו.
מכל הסיבות האלה, חשוב מאד לזכור ולהבין כל הגדרה שאתם נתקלים בה. בשפה הטבעית אפשר להבין מלים קשות מתוך ההקשר. במתמטיקה, כשלא זוכרים את ההגדרה, קשה - בוודאי לתלמיד חסר נסיון - לפענח למה הכוונה. מאידך, לא מספיק לזכור את ההגדרה באופן כזה שאפשר יהיה לפרוט אותה לרשימת התכונות המרכיבות אותה - כפי שראינו, נסיון כזה יגרום למשפטים שבהם המושג החדש מופיע להתארך במידה כזו שאי-אפשר יהיה להבין אותם כלל. (כשמנסים להמנע מהמושג "משפחה", מתברר ששבט הוא קבוצה של קבוצות של קופים, שבכל אחת מהן, לכל אגוז קוקוס השייך לאחד מחברי הקבוצה יש קוף אחר מאותה קבוצה שלו שייך אותו אגוז, וכך שאם יש שתי קבוצות שבכל אחת מהן, לכל אגוז קוקוס השייך לאחד מחברי הקבוצה יש קוף אחר מאותה קבוצה שלו שייך אותו אגוז, אז יש קבוצה נוספת שבה לכל אגוז קוקוס השייך לאחד מחברי הקבוצה יש קוף אחר מאותה קבוצה שלו שייך אותו אגוז, שבה יש קוף שהוא חבר לאחד הקופים מן הקבוצה הראשונה, וקוף שהוא חבר לאחד הקופים מן הקבוצה השניה).
כשאנו קוראים, איננו מפרקים כל מלה לאותיות - לאחר שצברנו נסיון-מה, אנחנו תופסים את המלה כמכלול. כך צריך גם להבין הגדרה חדשה: בתחילה יש לקרוא אותה בעיון ולוודא שכל האותיות מוכרות, אבל מיד אחר-כך צריך לנסות לדמיין איזו תכונה היא אמורה לתפוס. כדאי לבדוק את ההגדרה על מקרים קיצוניים: האם קוף יכול להיות חבר של עצמו? (כן; כל קוף הוא חבר של עצמו). מיהם החברים של קוף שאין לו אגוזי קוקוס? (כל הקופים שאין להם אגוזי קוקוס, ורק הם). האם יכולה להיות משפחה שיש בה רק קוף אחד? (לא). וכן הלאה.
לפעמים הגדרה דורשת עבודת הכנה. יכולנו להגדיר, עבור שבט של קופים, ש"מלך השבט הוא הקוף שיש לו אגוז משותף עם כל קוף בשבט", אבל השימוש בהא-הידיעה רומז שאכן קיים לכל שבט מלך (יחיד), וזה בכלל לא ברור. הגדרה כזו אינה תקפה, עד שנוכיח את הקיום והיחידות של המלך. באי מסודר, המושג "מנהיג השבט" מוגדר כראוי, לא משום שהתאמצנו להוכיח את קיומו, אלא משום שכך הגדרנו מהו אי מסודר; גם זה תעלול מתמטי שכיח למדי.
המבנה של הגדרות
להגדרות יש מבנה אחיד: דבר מסויים נקרא בשם מסויים, אם הוא מקיים תכונה מסויימת. לדוגמא, קבוצה של קופים היא משפחה אם היא מקיימת תכונה מסויימת; ההגדרה אינה יכולה לחול על מה שאיננו קבוצה של קופים; אין משמעות לשאלה "האם אגוז קוקוס זה הוא משפחה", משום שהגדרנו מהי משפחה רק עבור קבוצות של קופים. בהמשך הדרך נוכל גם להגדיר מתי אגוז קוקוס הוא משפחה - ואז, כאשר נתון ש-A היא משפחה, יהיה עלינו להבין מן ההקשר האם מדובר בקבוצה של קופים (שהיא משפחה), או באגוז קוקוס.
ההבחנה בין פרדיקט (שיש לו משתנים) לאטום (שהוא פרידקט ללא משתנים) חלה גם על הגדרות. מנקודת המבט הזו יש שני סוגי הגדרות:
- מתאים/לא-מתאים
- ההגדרה קובעת שעצמים (במחלקה מסויימת) העונים על תנאי ההגדרה ייקראו בשם מסויים. הגדרה כזו היא למעשה פרדיקט בן משתנה אחד, המקבל ערך אמת T כשמציבים במשתנה עצם העונה לתנאים, וערך אמת F בכל מקרה אחר. למשל,
- משולש הוא מצולע שיש לו שלושה קודקודים; או
- מצולע יקרא משולש אם יש לו שלושה קודקודים.
- (לכאורה צריך היה לומר "מצולע יקרא משולש אם ורק אם יש לו שלושה קודקודים"; כשכותבים הגדרה מקובל לנסח בקיצור, משום שממילא מדובר במושג חדש שלא היה לו קיום לפני ההגדרה).
- באותו אופן בדיוק, במקום לדבר על עצם בודד, אפשר לדבר על הקשר בין שני עצמים (או יותר). למשל, "אדם x הוא הבעלים של רכב y אם הרכב רשום על שמו במשרד התחבורה". ההגדרה הזו אינה מתייחסת לשאלה האם x הוא בעלים, באופן כללי, אלא רק לקשר בין x ל-y מסויימים. כמובן שעכשיו אפשר להגדיר "x הוא בעל רכב אם קיים y אשר x הוא הבעלים שלו".
- ההגדרה קובעת שעצמים (במחלקה מסויימת) העונים על תנאי ההגדרה ייקראו בשם מסויים. הגדרה כזו היא למעשה פרדיקט בן משתנה אחד, המקבל ערך אמת T כשמציבים במשתנה עצם העונה לתנאים, וערך אמת F בכל מקרה אחר. למשל,
- הגדרה מאפיינת
- הגדרה כזו דומה לסוג הראשון בכך שהיא מבוססת על פרדיקט, אלא שהיא מנצלת תכונה נוספת שלו: קיום ויחידות.
- נניח שלפרידקט יש משתנה אחד, כלומר, ההגדרה בודקת האם עצם מסויים עונה להגדרה או לא. אם אפשר להוכיח שיש עצם אחד ויחיד העונה להגדרה, אפשר להצמיד לשמו את הא הידיעה:
- המספר היחיד a שעבורו הנגזרת של הפונקציה
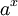 שווה לעצמה, נקרא בסיס הלוגריתמים הטבעי.
שווה לעצמה, נקרא בסיס הלוגריתמים הטבעי.
- המספר היחיד a שעבורו הנגזרת של הפונקציה
- לעצם המקיים הגדרה כזו אפשר לתת סימון מיוחד, שהוא חד-משמעי משום שהעצם מוגדר היטב. כאן בדיוק נכנסת "עבודת ההכנה" שהזכרנו באחת הפסקאות הקודמות.
- לעתים קרובות רוצים להגדיר מושג לא באופן אוניברסלי, אלא *עבור* עצם מסויים. למשל
- יהי a משולש. המעגל החוסם של a הוא המעגל היחיד העובר דרך שלושת הקודקודים של a.
- (מהי עבודת ההכנה כאן?). ההגדרה הזו קובעת - לכל משולש - איזה מעגל נקרא המעגל החוסם של המשולש הזה. הגדרה כזו מבוססת על פרדיקט בן שני מקומות -
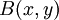 - שמקבל ערך אמת T אם ורק אם y מהווה מעגל חוסם של x. מכיוון ש-
- שמקבל ערך אמת T אם ורק אם y מהווה מעגל חוסם של x. מכיוון ש- 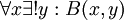 , אפשר לקרוא לאותו y (התלוי כמובן ב-x) בשם מיוחד - המעגל החוסם של x. שימו לב שכל מעגל חוסם איזשהו משולש (הצרינו זאת), ולכן איננו מגדירים כאן *איזה* מעגל נקרא מעגל חוסם (כמו בהגדרה מהסוג הראשון), אלא *מהו* המעגל החוסם של משולש מסויים.
, אפשר לקרוא לאותו y (התלוי כמובן ב-x) בשם מיוחד - המעגל החוסם של x. שימו לב שכל מעגל חוסם איזשהו משולש (הצרינו זאת), ולכן איננו מגדירים כאן *איזה* מעגל נקרא מעגל חוסם (כמו בהגדרה מהסוג הראשון), אלא *מהו* המעגל החוסם של משולש מסויים.
תרגיל. החליטו לאיזה סוג שייכות ההגדרות הבאות:
- חוג הוא מקומי אם יש לו אידיאל מקסימלי יחיד.
- המרכז של חוג הוא תת-החוג הגדול ביותר שכל אבריו מתחלפים עם כל אברי החוג.
המושג המוגדר
כללי המשחק המתמטי קובעים שאפשר להגדיר כל מושג שלא הוגדר בעבר. למשל, יכולנו לקבוע מהו "מספר מנצח", ולהשתמש מכאן ואילך במושג הזה כחלק מהשפה שלנו. ההחלטה כיצד לקרוא למושג מתמטי צומחת מתוך הקהילה המתמטית - למושג מוצלח יש סיכוי טוב יותר להיקלט ולהכנס לשימוש. שם המושג אמור לרמוז אל התוכן שלו - נעדיף למשל לקרוא למספר טבעי שאי אפשר לכתוב כמכפלת שני מספרים טבעיים קטנים יותר "מספר ראשוני" (משום שיש בו משהו יסודי, התחלתי), מאשר "מספר אולטרה סגול" או "גזר". כשתתקלו בהגדרות (הרבות) בהמשך הלימודים, נסו להבין מדוע נבחר שמו כל מושג - הדבר יקל עליכם לזכור אותם ולהבין מה היתה המוטיבציה שהובילה להגדרה.
כדי שלא להעמיס מונחים טכניים מסובכים (אולי בלטינית), בוחרים לתאר דברים במלים מוכרות. כך למשל, בתחום הנקרא "טופולוגיה", העוסק בצורה של קבוצות מרחביות, יש "קבוצות פתוחות" ו"קבוצות סגורות". יש קשר בין המושגים, אבל קבוצה יכולה להיות פתוחה וסגורה, או לא פתוחה ולא סגורה. דלת צריכה להיות פתוחה או סגורה, אבל השלילה של "U היא קבוצה פתוחה" איננה "U היא קבוצה סגורה", אלא "U איננה פתוחה": המושג שהוגדר מאבד את התכונות היומיומיות שלו.
משתנים המופיעים בהגדרה
בסעיף קודם ("משתנים ותחולתם") ציינו שלכל כמת יש אזור תחולה, שבתוכו המשתנה שלו מקבל משמעות אחידה. הדבר נכון גם (ובפרט) בהגדרות. למשל, אפשר להגדיר "מספר m הוא עצום, אם לכל מספר טבעי n<m, גם 2n<m" (תרגיל: הוכיחו שהמספר העצום היחיד הוא 1). שימו לב שבפעמים הבאות שבהן נרצה להשתמש במושג הזה, לא תהיה לאותיות m או n שום משמעות מיוחדת. למשל, אפשר לשאול "נניח ש-n עצום, האם גם 2n עצום?", ובמקרה כזה הצבה לא זהירה של ההגדרה (עם אותן אותיות) תגרום בלבול רב (בוודאי אסור להגיד ש"n הוא עצום אם לכל מספר טבעי n<n גם 2n<n"; איזה מספרים הם עצומים לפי ההגדרה הזו?). כדי למנוע התנגשויות, כדאי לפעמים להחליף את האותיות בהגדרה.
- תרגיל: מספר x הוא דו-ריבועי אם קיימים y,z כך ש-
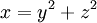 . נניח ש-x,y הם מספרים דו-ריבועיים. נסה להוכיח שהמכפלה xy היא דו-ריבועית. זהירות עם שמות המשתנים!
. נניח ש-x,y הם מספרים דו-ריבועיים. נסה להוכיח שהמכפלה xy היא דו-ריבועית. זהירות עם שמות המשתנים!
הוכחות
עד כאן עסקנו במבנה הצורני של טענות: בתרגום לשפה פורמלית, בפסוקים שקולים וכדומה. עיקר העניין במתמטיקה אינו בטענות סתם, אלא בטענות נכונות; ולא בטענות נכונות סתם, אלא באלו שאפשר להוכיח. אם כך, עלינו ללמוד להוכיח טענות: כיצד מוכיחים, כיצד כותבים הוכחה, כיצד בודקים הוכחה, ומהן השגיאות הנפוצות שמהן יש להמנע. התשובה שניתן כאן לשאלות האלה היא חלקית ועל קצה המזלג, ותגע ברעיונות הבסיסיים בלבד. ככל שתלמדו מושגים מתקדמים ותורות חדשות, תלמדו גם טכניקות מתקדמות להוכחת טענות. ראו כאן רשימה קצרה בנושא כתיבה מתמטית. דבר אחד חשוב לזכור מן הרגע הראשון: הוכחות מתמטיות כותבים בעברית תקנית. מותר להשתמש בסימנים מתמטיים לפי הצורך, אבל בלי הקפדה על שפה תקינה, על פיסוק נכון ועל בניה שיטתית של הפסקאות, אי אפשר יהיה להבין את ההוכחות שלכם.
פסוק שיש לו הוכחה מתמטית נקרא משפט. המשפטים מבוססים על משפטים קודמים להם וכן הלאה, עד שמגיעים אל האקסיומות היסודיות. בכל תורה מתמטית יש אקסיומות (למעט הלוגיקה הפסוקית, שבה אין בהן צורך). חלק מן הפסוקים האמיתיים שפגשנו קודם לכן נחשבים לאקסיומות בכל מערכת מתמטית.
בלוגיקה הקלאסית מנתחים את ה"טיעון הלוגי", שהוא אוסף פסוקים (הנחות) ופסוק יחיד (מסקנה) הנובעת לוגית מההנחות. טיעון לוגי הוא תקף אם המסקנה נובעת לוגית מההנחות, ואינו תקף אחרת. בעת בדיקת תקיפות טיעון יש לוודא כי המסקנה אכן נובעת מההנחות, ולא אם ההנחות שקריות או אמיתיות. מתברר שאפשר לתרגם כל טיעון לוגי תקף לטיעון בעל מבנה מיוחד, הנקרא מודוס פוננס, ולכן נסתפק בהצגת המבנה הזה, שהוא החוליה שממנה מחברים כל הוכחה.
מודוס פוננס
הוכחה פורמלית של פסוק P היא רצף של פסוקים 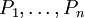 שכל אחד מהם הוא או אקסיומה, או שאפשר לגזור אותו באופן פורמלי מפסוקים קודמים: אם
שכל אחד מהם הוא או אקסיומה, או שאפשר לגזור אותו באופן פורמלי מפסוקים קודמים: אם 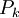 אינו אקסיומה, צריכים להיות קיימים
אינו אקסיומה, צריכים להיות קיימים 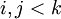 כך ש-
כך ש- 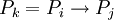 .
.
הגזירה מתבססת כאן על הכלל הלוגי היסודי הנקרא מודוס פוננס: מ- 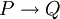 ו-
ו- 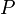 אפשר לגזור (כלומר להסיק את)
אפשר לגזור (כלומר להסיק את) 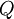 .
.
בלימודי המתמטיקה תפגשו הוכחות פורמליות לעתים נדירות ביותר. בדרך כלל מסתפקים בהוכחה מדוקדקת שאמנם אינה פורמלית, אבל אפשר לתרגם אותה להוכחה פורמלית. בכל שלב מהותי של ההוכחה תוכלו לזהות שמגיעים אל המסקנה מתוך שתי עובדות שהוכחו קודם לכן: ההנחה, והטענה שההנחה גוררת את המסקנה.
שימו לב. מהטענה 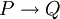 לא נובע P, ולא נובע Q, אלא רק שאם P אז Q. תנו דוגמא מפורשת לכך.
לא נובע P, ולא נובע Q, אלא רק שאם P אז Q. תנו דוגמא מפורשת לכך.
תרגיל. נניח שהמשפט הבא הוא אמיתי: "כאשר אני בכושר אני מסוגל לרוץ 10 קילומטר".
- נניח עוד כי "כעת איני בכושר" האם אני מסוגל לרוץ 10 קילומטר? אם לא, הוכח (באמצעות הצרנה).
- נניח שאיני מסוגל לרוץ 10 קילומטר, האם אני בכושר? הוכח.
- נניח שאני מסוגל לרוץ 10 קילומטר, האם אני בכושר? הוכח.
הוכחה בדרך השלילה
הוכחה בדרך השלילה נבנית על הטאוטולוגיה הפשוטה 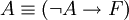 . כלומר, כדי להוכיח טענה A, מספיק להוכיח ששלילת הטענה הזו מביאה לסתירה, F. כשנתקעים בהוכחה, לפעמים מועיל להניח שהמסקנה שאליה רוצים להגיע אינה נכונה, על-מנת שיהיה קל יותר ליצור מסקנות ביניים חדשות, עד שנגיע לסתירה המיוחלת.
. כלומר, כדי להוכיח טענה A, מספיק להוכיח ששלילת הטענה הזו מביאה לסתירה, F. כשנתקעים בהוכחה, לפעמים מועיל להניח שהמסקנה שאליה רוצים להגיע אינה נכונה, על-מנת שיהיה קל יותר ליצור מסקנות ביניים חדשות, עד שנגיע לסתירה המיוחלת.
דוגמא:
- רוצים להוכיח שיש אינסוף מספרים ראשוניים. נניח בשלילה שיש רק מספר סופי של ראשוניים
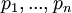 ; אז המספר
; אז המספר 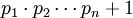 אינו מתחלק באף מספר ראשוני, ולכן הוא מוכרח להיות ראשוני; אבל הוא גדול מכל מספר ראשוני, וזו סתירה. (הוכחה זו נמצאת בספרו בן ה-2300 שנה של אוקלידס, "יסודות").
אינו מתחלק באף מספר ראשוני, ולכן הוא מוכרח להיות ראשוני; אבל הוא גדול מכל מספר ראשוני, וזו סתירה. (הוכחה זו נמצאת בספרו בן ה-2300 שנה של אוקלידס, "יסודות"). - רוצים להוכיח ששורש 2 אינו מספר רציונלי (כלומר שבר בעל מונה ומכנה שלמים). נניח בשלילה ששורש שתיים הוא רציונלי. אז קיים שבר מצומצם
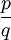 כך ש
כך ש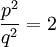 . לכן
. לכן 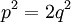 לכן
לכן 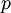 זוגי ולכן הוא מהצורה
זוגי ולכן הוא מהצורה 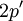 ולכן מתקיים
ולכן מתקיים 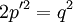 ולכן
ולכן 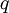 זוגי בסתירה לכך שהשבר היה מצומצם.
זוגי בסתירה לכך שהשבר היה מצומצם. - נוכיח שאין מספר רציונלי חיובי מינימלי. נניח בשלילה ש
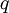 הינו המספר הרציונאלי הקטן ביותר הגדול מאפס. אזי
הינו המספר הרציונאלי הקטן ביותר הגדול מאפס. אזי 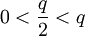 הוא מספר רציונאלי, בסתירה להנחת המינימליות.
הוא מספר רציונאלי, בסתירה להנחת המינימליות.
לפעמים תפגשו הוכחות המסתיימות, למשל, ב"ולכן x הוא אדום, בסתירה". רצוי, בפרט כשההוכחה מתארכת, להשלים ולומר בסתירה למה (לכך ש-x אינו אדום? לכך שיש רק מספר אדום אחד, השווה ל-x+6?). מכיוון שאנו מניחים שהמתמטיקה עצמה אינה כוללת סתירות, העובדה שהצלחנו להוכיח שתי טענות סותרות פירושה שאחת ההנחות שלנו אינה נכונה.
"בלי הגבלת הכלליות"
דוגמא. בין המספרים השלמים מוגדרת פעולת כפל, ומוגדר יחס של חלוקה: 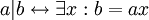 . מספר p, שאינו אפס ואינו מחלק את 1, הוא ראשוני אם
. מספר p, שאינו אפס ואינו מחלק את 1, הוא ראשוני אם 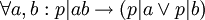 . מספר p, שאינו אפס ואינו מחלק את 1, הוא אי-פריק אם
. מספר p, שאינו אפס ואינו מחלק את 1, הוא אי-פריק אם 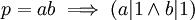 . נוכיח שכל מספר ראשוני הוא אי-פריק: יהי p מספר ראשוני. כדי להוכיח שהוא אי-פריק, עלינו להראות שאם p=ab אז a|1 או b|1. נניח, אם כך, ש- p=ab. מכיוון ש- ab=p*1, p|ab ומכיוון ש-p ראשוני, בלי הגבלת הכלליות, אפשר להניח ש- p|a. אבל אז קיים x כך ש- a=px=abx, ומכיוון ש-
. נוכיח שכל מספר ראשוני הוא אי-פריק: יהי p מספר ראשוני. כדי להוכיח שהוא אי-פריק, עלינו להראות שאם p=ab אז a|1 או b|1. נניח, אם כך, ש- p=ab. מכיוון ש- ab=p*1, p|ab ומכיוון ש-p ראשוני, בלי הגבלת הכלליות, אפשר להניח ש- p|a. אבל אז קיים x כך ש- a=px=abx, ומכיוון ש-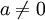 (אחרת p=0), אפשר לצמצם ולקבל bx=1, ומכאן b|1.
(אחרת p=0), אפשר לצמצם ולקבל bx=1, ומכאן b|1.
במלים "בלי הגבלת הכלליות" מותר להשתמש כשמבצעים הנחה שאינה מתחייבת מן הנתונים (במקרה שלנו, הנחנו ש-p|a, בעוד שכל מה שידוע לנו הוא ש-p|a או p|b; אולי דווקא p|b, ואז לא ידוע האם p|a?), ובכל זאת ברור שהיא מכסה את כל האפשרויות. במקרה שלנו אפשר היה לנסח כך: ראינו ש-p|ab, ומכיוון ש-p ראשוני, הוא מחלק את אחד הגורמים; אם הוא מחלק את b, נחליף את שמות הגורמים, וכך אפשר יהיה להניח שבכל מקרה p|a.
הוכחת טענות מכומתות
פסוק ללא כמתים אפשר להוכיח באמצעות טבלת אמת. כל הפסוקים מסוג זה נחשבים לאמיתות טריוויאליות, ולכן הם נמצאים בשכבה הראשונה של מאגר האקסיומות. את ההוכחה של פסוקים מורכבים יותר אפשר לתפוס כמשחק בין שני צדדים: ה"מוכיח", וה"יריב".
- כדי להוכיח טענה מהסוג
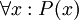 , על המוכיח להראות את אמיתות הטענה
, על המוכיח להראות את אמיתות הטענה 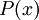 , וזאת לכל x *שבחר היריב*. היריב עשוי לבחור x שעבורו הוכחת הטענה קשה יותר. למוכיח אסור לבחור את x בעצמו, משום שהוא צריך להוכיח את הטענה לכל x.
, וזאת לכל x *שבחר היריב*. היריב עשוי לבחור x שעבורו הוכחת הטענה קשה יותר. למוכיח אסור לבחור את x בעצמו, משום שהוא צריך להוכיח את הטענה לכל x. - כדי להוכיח טענה מהסוג
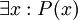 , המוכיח צריך להראות את אמיתות הטענה
, המוכיח צריך להראות את אמיתות הטענה 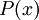 עבור x כלשהו. הדרך הקלה והבטוחה ביותר לעשות זאת היא *להצביע* על x שעבורו הטענה נכונה; זוהי הוכחה קונסטרוקטיבית. יש גם הוכחות לא קונסטרוקטיביות, אבל בשלבי הלימודים הראשונים תתקלו בהן רק לעתים רחוקות.
עבור x כלשהו. הדרך הקלה והבטוחה ביותר לעשות זאת היא *להצביע* על x שעבורו הטענה נכונה; זוהי הוכחה קונסטרוקטיבית. יש גם הוכחות לא קונסטרוקטיביות, אבל בשלבי הלימודים הראשונים תתקלו בהן רק לעתים רחוקות.
בדרך כלל המשחק כולל יותר משלב אחד. למשל, כדי להוכיח "לכל x חיובי קיים y חיובי הקטן ממנו", עלינו לאפשר ליריב לבחור x כרצונו; אחר-כך עלינו להראות שקיים y הקטן מן ה-x הזה, וזאת נעשה על-ידי בחירת y מתאים (למשל: 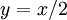 ). אפשר לכתוב זאת כך:
). אפשר לכתוב זאת כך:
- עלינו להוכיח שלכל
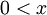 יש
יש 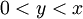 . יהי
. יהי 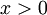 (היריב בוחר x *כרצונו*). נבחר
(היריב בוחר x *כרצונו*). נבחר 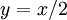 , ואז
, ואז 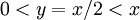 (כאן אנו בודקים שעבור y שבחרנו, הטענה אכן מתקיימת).
(כאן אנו בודקים שעבור y שבחרנו, הטענה אכן מתקיימת).
להלן דוגמא דומה, ושגויה בתכלית:
- רוצים להוכיח שלכל n שלם קיים m (שלם) כך ש-
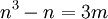 . יהי n מספר שלם. נבחר m כך שמתקיים
. יהי n מספר שלם. נבחר m כך שמתקיים 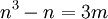 -- מה שהיה להוכיח.
-- מה שהיה להוכיח.
בדוגמא הזו לא *הוכחנו* שקיים m שלם המקיים את התנאי: הסתפקנו בהצהרה שהוא קיים, ו"בחרנו" אותו. זו אינה הוכחה. הבחירה צריכה להיות מפורשת, על-מנת שכל קורא (וכל בודק מבחנים) יוכל להשתכנע שאותו m אכן קיים.
נזכיר שהספריה L מוצלחת אם יש בה אגף S כך שלכל נושא t יש באגף מדף s, כך שכל ספר x ב-s עוסק בנושא t; הגדרה זו כוללת ארבעה כמתים - ובמתמטיקה יש לא מעט מושגים יסודיים שהגדרתם היא ברמת המורכבות הזו לפחות. כדי להוכיח שספריה נתונה היא מוצלחת, עלינו להצביע על האגף המוצלח; לתת ליריב לבחור נושא; לבחור את המדף, ולהראות שכל ספר על המדף הזה אכן עוסק בנושא הדרוש. תרגיל. תאר את מהלך המשחק המוכיח שספריה מסויימת אינה מוצלחת.
סדר הפעולות במשחק חשוב ביותר. לאחר שבחרנו את האגף S, היריב עשוי לבחור 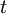 התלוי ב-S; ואז נוכל בתורנו לבחור את המדף כפונקציה של t ושל
התלוי ב-S; ואז נוכל בתורנו לבחור את המדף כפונקציה של t ושל 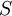 (אבל לא של x, שאינו מוגדר בכלל בשלב הזה!).
(אבל לא של x, שאינו מוגדר בכלל בשלב הזה!).
להלן כמה טכניקות הוכחה שכיחות.
- "מספיק להוכיח ש-": לפעמים הדרך הקצרה ביותר להוכיח טענה מסויימת היא הוכחת טענה חזקה יותר. זהו שימוש ישיר במודוס פוננס: במקום להוכיח את Q, אנו מוכיחים את P, כאשר הטענה
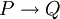 ידועה מראש. למשל, כדי להוכיח "קיים מספר ראשוני הגדול מ-
ידועה מראש. למשל, כדי להוכיח "קיים מספר ראשוני הגדול מ-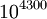 ", מספיק להוכיח שקיימים אינסוף ראשוניים.
", מספיק להוכיח שקיימים אינסוף ראשוניים.
תרגילים.
- השתמש בפרדיקט
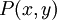 (אדם x חובב חיות מסוג y) כדי להצרין את הטענה "כל אדם החובב חיות, חובב לפחות שני סוגים שלהן". מה יש לעשות כדי להוכיח טענה כזו? מה יש לעשות כדי להפריך אותה?
(אדם x חובב חיות מסוג y) כדי להצרין את הטענה "כל אדם החובב חיות, חובב לפחות שני סוגים שלהן". מה יש לעשות כדי להוכיח טענה כזו? מה יש לעשות כדי להפריך אותה? - מרחב הוא קומפקטי אם לכל כיסוי פתוח שלו, יש תת-כיסוי סופי. לצורך העניין אין זה חשוב מהו כיסוי פתוח של מרחב, מהו תת-כיסוי, ומתי תת-כיסוי הוא סופי; נעיר רק שכל תת-כיסוי הוא בעצמו כיסוי, והתכונה "a הוא תת-כיסוי של b" היא פרדיקט דו-מקומי (אם תרצו, אתם יכולים להצרין את כל הנתונים האלה). קבע אלו מהטענות הבאות נכונה:
- המרחב K הוא קומפקטי אם ורק אם יש לו כיסוי סופי.
- המרחב K הוא קומפקטי אם ורק אם יש לו כיסוי פתוח שיש לו תת-כיסוי סופי.
- המרחב K אינו קומפקטי אם ורק אם יש לו כיסוי פתוח שאין לו תת-כיסוי סופי.
- בחר אחת מההגדרות החלופיות שהוצעו לעיל, שלכאורה אינה שקולה לקומפקטיות. יתכן שההגדרות שקולות בכל זאת, משום שיש תכונות נוספות של כיסויים פתוחים שלא לקחתם בחשבון. אלו תכונות של כיסויים פתוחים יספיקו כדי לקבוע בכל מקרה שההגדרות שקולות?
- דוגמא. לפני המאפיה עומדים בתור אינסוף אנשים - ראשון, שני, שלישי וכן הלאה. האם אפשר לחלק לאנשים אינסוף כובעים, כך שכל חובש כובע גבוה לפחות כמו חובש הכובע שלפניו, או כך שכל חובש כובע נמוך לפחות כמו חובש הכובע שלפניו? (לפני שתגשו לפתור את השאלה, שימו לב לכך שהטענה "אפשר לחלק לאנשים אינסוף כובעים, כך שכל חובש כובע גבוה לפחות כמו חובש הכובע שלפניו, או נמוך לפחות כמו חובש הכובע שלפניו" היא טריוויאלית ואינה שקולה לטענה שאנו מנסים להוכיח).
פתרון. כן. נגדיר איש נישא בתור איש שאין אחריו אף אדם גבוה יותר. אם קיימים אינסוף נישאים בתור, אזי הם מהווים תור אינסופי שאינו עולה. אם לעומת זאת, יש רק מספר סופי של נישאים, נסלק את כל האנשים מהראשון בתור ועד לאחרון הנישאים. נשארנו עם אינסוף אנשים לא נישאים, כלומר שלכל אחד מהם יש מישהו הגבוה ממנו. נתחיל בראשון בתור, נעבור לגבוה ממנו, נעבור משם לגבוה ממנו, וכן הלאה, כך שיתקבל תור אינסופי שאינו יורד.
הפרכה
הפרכה של טענה אינה אלא הוכחה שהטענה אינה נכונה.
- הפרכה על-ידי דוגמא נגדית: כדי להפריך את הטענה
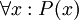 , יש להראות שקיים x שעבורו הטענה
, יש להראות שקיים x שעבורו הטענה 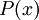 אינה נכונה. גם כאן, הדרך השכיחה ביותר היא להצביע על ערך מסויים של x שעבורו הטענה אינה נכונה.
אינה נכונה. גם כאן, הדרך השכיחה ביותר היא להצביע על ערך מסויים של x שעבורו הטענה אינה נכונה. - מאידך, כדי להפריך את הטענה
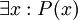 , יש *להוכיח* שלכל x, הטענה
, יש *להוכיח* שלכל x, הטענה 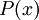 אינה נכונה.
אינה נכונה.
- כידוע, שני דברים השווים לדבר שלישי שווים ביניהם (בשפה המתמטית, זוהי "תכונת הטרנזיטיביות של יחס השוויון"). הפרך את הטענה הבאה: (כל) שני דברים השונים מדבר שלישי, שונים זה מזה.
הוכח או הפרך: שאלה כמו "הוכח או הפרך - אם p ראשוני אז הוא אי-זוגי" שואלת למעשה "נכון לא נכון - אם p ראשוני אז הוא אי-זוגי", וגם רומזת מה יש לעשות בשני המקרים: אם הטענה נכונה, יש לספק לה הוכחה, ואם היא לא נכונה, יש להפריך אותה, כמעט תמיד באמצעות דוגמא נגדית ("טענה זו אינה נכונה משום ש-p=2 הוא ראשוני אבל אינו אי-זוגי"). פעמים רבות הטענה היא מהצורה "לכל a, מתקיים 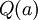 ". דוגמא שבה הטענה מתקיימת אינה יכולה לבוא במקום הוכחה, משום שהטענה היא ש-
". דוגמא שבה הטענה מתקיימת אינה יכולה לבוא במקום הוכחה, משום שהטענה היא ש-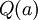 לכל a ולא רק עבור a נחמדים במיוחד; מצד שני, כדי להפריך טענה כזו, אין שום צורך להראות שהיא נכשלת לכל a; מספיק למצוא a מסויים שעבורו היא נכשלת. כמובן, אם
לכל a ולא רק עבור a נחמדים במיוחד; מצד שני, כדי להפריך טענה כזו, אין שום צורך להראות שהיא נכשלת לכל a; מספיק למצוא a מסויים שעבורו היא נכשלת. כמובן, אם 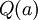 נכונה לפעמים ושגויה לפעמים, אז הטענה "לכל a מתקיים
נכונה לפעמים ושגויה לפעמים, אז הטענה "לכל a מתקיים 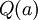 " שגויה (ולא "שגויה לפעמים!").
" שגויה (ולא "שגויה לפעמים!").
שיטות לפתרון בעיות מתמטיות
אין שיטות בטוחות לפתרון בעיות מתמטיות (בעיות שיש שיטה לפתרונן הן, למעשה, פתורות). בכל זאת, יש לא מעט רעיונות כלליים ואסטרטגיות שיסייעו לכם לתקוף שאלות הוכחה ביעילות. חלק מהעצות סותרות זו את זו; אבל ממילא כל אחת מהן ישימה במקרים אחרים.
- הבינו את השאלה. אין טעם להתחיל לפתור בעיה לפני שהבנתם את המושגים המופיעים בה ואת הטענה שיש להוכיח.
- האם זה הגיוני בכלל? לפני שאתם מנסים להוכיח טענה, נסו להפריך אותה! כשלון נסיונות ההפרכה יעזור לכם להבין מדוע הטענה נכונה אחרי הכל.
- השוו לבעיות דומות. לפעמים אפשר לאמץ את השיטה מן הבעיה האחרת כפי שהיא; בפעמים אחרות, הבנת הסיבה לכך שהשיטה אינה עובדת יכולה לסייע בגילוי האלטרנטיבות.
- השוו את הנתונים למסקנות. לפעמים יש רק מספר דרכים מצומצם להגיע מן הנתונים אל המטרה.
- תכננו לפני שאתם כותבים. אין טעם למלא עמוד וחצי בתאור מדוקדק של הצעד הראשון בפתרון, כשאין לכם מושג איך להמשיך משם.
- שחקו עם הפרטים. נסו להחליש את הטענה על-ידי החלשת המסקנה או חיזוק ההנחות. עשו זאת באופן מתון, כדי שהבעיה המוחלשת לא תהיה חסרת ערך.
- בנו השערות ביניים. חישבו כך - אם הייתי יודע שהמצב הוא כך-וכך, הייתי יכול להוכיח את הטענה בעזרת נימוק כזה-וכזה; כעת - האם השערת הביניים נובעת מן ההנחות?
- הדגימו. כדי להבין טוב יותר את הבעיה, נסו להפעיל אותה על דוגמא טיפוסית.
- כיתבו בשפה ברורה. שימוש נאות בשפה הוא תנאי להעברת מידע, לא רק מכם אל המתרגל או המרצה, אלא גם מכם אל עצמכם בעוד זמן-מה.
- דייקו. הוכחה תקינה צריכה להיות מדוייקת בכל פרטיה.
שגיאות נפוצות
שגיאות בהוכחה נדירות למדי באולמות ההרצאה, אבל עד שמתרגלים לחומר ולומדים אותו היטב, הן די שכיחות מחוץ להם. היכרות טובה עם שגיאות נפוצות יכולה לעזור לכם להמנע מהן.
אחת השגיאות הנפוצות היא החלפת סדר כמתים. יש הבדל עצום בין "לכל סיר יש מכסה המתאים לו", לבין "יש מכסה המתאים לכל הסירים". הצרינו את שתי הטענות, וקבעו איזו מהן גוררת את השניה.
שגיאה פופולרית נוספת היא הנחת המבוקש. צריך להוכיח שלכל נחש יש ארבע שיניים. יהי x נחש. בתחילת השאלה כתוב במפורש - "לכל נחש יש ארבע שיניים"; לכן יש ל-x ארבע שיניים, מש"ל.
לפעמים הדרך המובנת מאליה, לכאורה, להוכיח טענה מסויימת - נכשלת, ויש למצוא דרך אחרת. כשלון ההוכחה הראשונה אינו מעיד על כך שהטענה שגויה.
שגיאה נוספת, הנובעת מחוסר הבנה או חוסר תשומת לב, היא שימוש ב"טאוטולוגיות" שגויות.
- כל החתולים צהובים. רוצים להראות ש-c חתול. לשם כך מראים שהוא צהוב.
- רוצים להפריך את הטענה שלפיה כל החולצות אדומות. מצביעים בארשת נצחון על בגד אדום, ושוכחים לבדוק שזו חולצה.
- הפעלת תנאי מספיק כאילו היה הכרחי: אם הוא יודע אלגברה לינארית, סימן שהוא חכם. הוא אינו יודע אלגברה לינארית, ומכאן שאינו חכם.
- רוצים להוכיח שכל הסוסים שחורים. רוזיננטה הוא סוס. הבה נוכיח שהוא שחור.
- קריאה סלקטיבית: כשהפסוק הלוגי נעשה ארוך ומסובך (אם לכל x קיים y כך ש..., אז ...), יש נטיה לשלוף קטע ממנו ולהתייחס אליו בלבד. זיכרו שגזירה במספריים אינה אופרטור חוקי בלוגיקה.