הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/6"
(←דוגמא) |
(←קואורדינטות) |
||
| שורה 1: | שורה 1: | ||
==קואורדינטות== | ==קואורדינטות== | ||
| − | |||
| − | |||
משפט: יהא V מ"ו מעל שדה F, יהי <math>B=\{v_1,...,v_n\}</math> בסיס ל-V ויהי <math>v\in V</math> וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים <math>v=a_1v_1+...+a_nv_n=b_1v_1+...+b_nv_n</math> אזי בהכרח <math>\forall i:a_i=b_i</math>. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים <math>a_i-b_i</math>.) | משפט: יהא V מ"ו מעל שדה F, יהי <math>B=\{v_1,...,v_n\}</math> בסיס ל-V ויהי <math>v\in V</math> וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים <math>v=a_1v_1+...+a_nv_n=b_1v_1+...+b_nv_n</math> אזי בהכרח <math>\forall i:a_i=b_i</math>. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים <math>a_i-b_i</math>.) | ||
גרסה מ־21:11, 29 ביולי 2011
קואורדינטות
משפט: יהא V מ"ו מעל שדה F, יהי 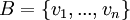 בסיס ל-V ויהי
בסיס ל-V ויהי 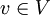 וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים
וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים 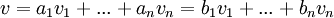 אזי בהכרח
אזי בהכרח 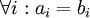 . (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים
. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים 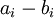 .)
.)
הגדרה: יהיו V,B וv כמו במשפט. אזי וקטור הקואורדינטות של v לפי בסיס B, מסומן ![[v]_B\in\mathbb{F}^n](/images/math/4/8/d/48d175f864d880e25a45feb85ad8c94e.png) מוגדר להיות
מוגדר להיות ![[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}](/images/math/f/9/5/f95c4d5b167fb4c2880885415ca0e149.png) כאשר
כאשר 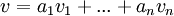 ההצגה הלינארית היחידה הקיימת לפי המשפט.
ההצגה הלינארית היחידה הקיימת לפי המשפט.
חשוב לזכור ![[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}](/images/math/f/9/5/f95c4d5b167fb4c2880885415ca0e149.png) אם"ם
אם"ם 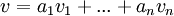
תרגיל קל אבל חשוב הוא להראות שלכל בסיס B מתקיים ש 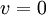 אם"ם
אם"ם ![[v]_B=0](/images/math/a/a/c/aac616b8c08680fd2fb1e1e5cccb8134.png) .
.
הערה: במרחבים הוקטוריים שאנו נעבוד איתם יש בסיסים סטנדרטיים. הייחוד של הבסיסים הסטנדרטיים הוא שקל מאד לחשב קואורדינטות לפיהם. נסתכל במרחבים וקטורים ובבסיסים הסטנדרטיים שלהם:
| מרחב וקטורי | בסיס סטנדרטי |
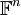
|
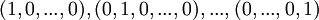
|
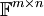
|

|
![\mathbb{F}_n[x]](/images/math/5/0/4/504c6115c35647a079e43b17f4468bef.png)
|
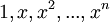
|
דוגמא.
חשב את הקואורדינטות של הוקטור 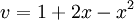 לפי הבסיס הסטנדרטי S של
לפי הבסיס הסטנדרטי S של ![\mathbb{R}_3[x]](/images/math/8/4/e/84ef8e18caf28275bb31fb78edc3a348.png) . למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס:
. למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס:
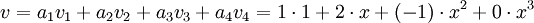 .
.
לפיכך ![[v]_S=(1,2,-1,0)](/images/math/7/2/c/72ce9c7c6545dbb68aececb179bddf8c.png) .
.
דוגמא.
חשב את הקואורדינטות של הוקטור 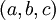 לפי הבסיס הסטנדרטי S של
לפי הבסיס הסטנדרטי S של 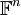 . קל לראות ש
. קל לראות ש ![[v]_S = (a,b,c)](/images/math/1/6/0/160aaa76dd5f1b407f9a424f38ca36ad.png) .
.
תרגיל
יהא V מ"ו ויהי B בסיס לו. יהיו 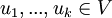 וקטורים כלשהם. הוכח:
וקטורים כלשהם. הוכח:
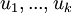 בת"ל אם"ם
בת"ל אם"ם ![[u_1]_B,...,[u_k]_B](/images/math/e/b/4/eb4b5b4e735834a276365d7282070e08.png) בת"ל
בת"ל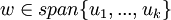 אם"ם
אם"ם ![w\in span\{[u_1]_B,...,[u_k]_B\}](/images/math/1/a/5/1a56d8e74b2ce1157db44ff9c25f4039.png)
נוכיח תרגיל זה בהמשך, לאחר שנלמד על העתקות לינאריות. כעת נניח שהוא נכון ונתרכז בכלי החישובי המשמעותי שקיבלנו; כל בדיקה/חישוב של תלות לינארית או פרישה בכל מרחב וקטורי (מטריצות, פולינומים, פונקציות) יכול בעצם להעשות במרחב הוקטורי המוכר והנוח 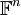 .
.
דוגמא.
האם הפולינומים 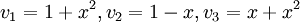 תלויים לינארית?
תלויים לינארית?
דבר ראשון, נעבור למרחב הקואורדינטות. מכיוון שבחירת הבסיס היא לשיקולנו, נבחר את הבסיס הסטנדרטי S של הפולינומים איתו קל לעבוד. מתקיים ש ![[v_1]_S=(1,0,1),[v_2]_S=(1,-1,0),[v_3]=(0,1,1)](/images/math/8/2/f/82f4358d3e0f0b5e6e7ea98bae8c8ff9.png)
הוכחנו בשיעור שעבר שוקטורים "רגילים" ת"ל אם"ם המטריצה שהם השורות שלה אינה הפיכה אם"ם הצורה המדורגת של המטריצה מכילה שורת אפסים. לכן, נשים את וקטורי הקואורדינטות בשורות מטריצה ונדרג.
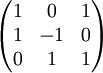
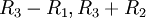
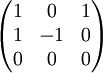
לכן וקטורי הקואורדינטות תלויים לינארית ולכן הפולינומים עצמם תלויים לינארית. נסכם את התהליך:
אלגוריתם לבדיקת תלות לינארית בין וקטורים
- הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים
- שים את וקטורי הקואורדינטות בשורות מטריצה A
- הבא את המטריצה לצורה מדורגת
- אם באיזה שלב קיבלת שורת אפסים סימן שהוקטורים תלויים לינארית
- אם הגעת לצורה מדורגת ללא שורת אפסים סימן שהוקטורים בלתי תלויים לינארית